3.3.5. Скорости и ускорения точек вращающегося тела

Р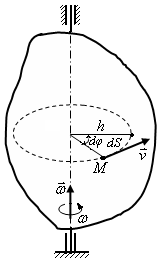 ассмотрим какую-нибудь точку твердого тела, находящуюся на расстоянии от оси вращения (рис. 3.6). По определению вращательного движения твердого тела точка описывает окружности в плоскости, перпендикулярной к оси вращения и с центром, лежащем на оси вращения. Если за время Δt тело совершит поворот на угол dφ, то точка М при этом совершит элементарное перемещение вдоль своей траектории .Тогда скорость точки вдоль траектории равна

Р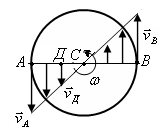 ис. 3.6 . (3.11) Скорость , в отличие от угловой скорости тела ω, называется линейной или окружной скоростью точки М. Таким образом, линейная скорость точки М вращающегося твердого тела численно равна произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Рис. 3.7 Так как для всех точек тела ω имеет в данный момент времени одно и то же значение, то из (3.11) следует, что линейные скорости точек вращающегося тела пропорциональны их расстояниям до оси вращения (рис. 3.7).

Для нахождения ускорения точки воспользуемся формулами:

, .

В нашем случае , тогда:

, . (3.12)

Полное ускорение точки :

. (3.13)

К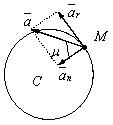 асательное ускорение направлено по касательной к траектории в сторону движения, если движение ускоренное и в противоположную сторону, если движение замедленное.

Нормальное ускорение всегда направлено по радиусу h к оси вращения (рис. 3.8). Отклонение вектора полного ускорения от радиуса, описываемой точкой

Рис. 3.8 окружности пределяется углом ,

. (3.14)

Так как угловые скорость ω и ускорение ε одинаковы для всех точек тела в данный момент, то из (3.13) следует, что ускорение всех точек вращающегося тела пропорциональны их расстоянием до оси вращения и образуют тот же угол μ с радиусом окружности.

3.3.6. Векторные выражения вращательной скорости, вращательного и центростремительного ускорений

Введем понятия векторов угловой скорости и углового ускорения .

У 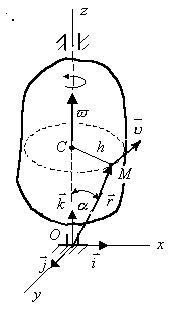словимся векторы угловой скорости и углового ускорения откладывать от любой точки на оси вращения, направляя их по оси. Вектор угловой скорости направляем таким образом, что бы смотря навстречу этому вектору, видеть вращение тела, происходящим против стрелки часов (рис. 3.9). На схемах угловую скорость и угловое ускорение часто изображают в виде круговых стрелок. Круговая стрелка для угловой скорости ω показывает направление изменения угла

Рис. 3.9 поворота, а круговая стрелка для углового ускорения ε показывает направление изменения угловой скорости. Направление вектора углового ускорения совпадает с направлением вектора при ускоренном вращении и противоположно ему при замедленном вращении.

Изобразим вектор угловой скорости и радиус-вектор точки относительно произвольной точки О оси вращения и вращательную скорость этой точки (рис. 3.9).

Модуль вращательной скорости равен

,

где - α угол между векторами , .

Модуль векторного произведения равен

.

Сопоставляя значения модулей v и , устанавливаем, что модуль вращательной скорости равен модулю векторного произведения

.

В ектор направлен перпендикулярно к плоскости треугольника СОМ, то есть перпендикулярно плоскости векторов сомножителей и . Если смотреть навстречу , можно видеть поворот вектора к на угол α, совершающийся против движения часовой стрелки. Таким образом, направление вращательной скорости совпадает с направлением вектора векторного произведения .

Векторы и имеют одинаковые модули и направления, следовательно, они равны между собой

, (3.15)

то есть, вращательная скорость точки твёрдого тела, вращающегося вокруг неподвижной оси, равна векторному произведению условной скорости тела на радиус-вектор этой точки относительно любой точки оси вращения.

С помощью определителя (3.15) можно записать в таком виде:

. (3.16)

О тсюда определяются проекции вращательной скорости точки на оси координат:

,

, (3.17)

.

Эти формулы были получены Эйлером в 1765 г. и называются формулами Эйлера.

В случае, когда ось Oz совпадает с осью вращения AB, имеем: ω_x= 0, ω_y= 0, ω_z=ω, откуда

, , .

Для получения векторных выражений , продифференцируем по времени выражение ; тогда получим

,

здесь , .

Подставляя эти значения, получим

. (3.18)

Покажем, что первое слагаемое есть касательное (вращательное) ускорение, а второе слагаемое - нормальное (центростремительное) ускорение.

Модуль касательного ускорения равен , где α угол между радиус-вектором и вектором углового ускорения (рис. 3.10). Направлен вектор касательного ускорения по касательной к траектории в точке М.

Модуль векторного произведения равен

.

Направлен вектор векторного произведения перпендикулярно плоскости треугольника СОМ, то есть плоскости векторов сомножителей и . Если смотреть навстречу вектору (рис. 3.10, а), то можно видеть поворот вектора к вектору на угол α, совершающимся против движения часовой стрелки.

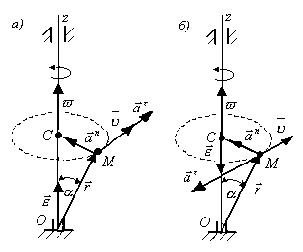
Рис. 3.10

Сопоставляя значения модулей и направлений векторов и видим, что модули их равны и направления одинаковы. Следовательно, эти векторы равны

. (3.19)

Таким образом, касательное (вращательное) ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора углового ускорения тела на радиус-вектор этой точки относительно любой точки оси.

Модуль нормального (центростремительного) ускорения

.

Модуль векторного произведения равен

,

так как при . Составляя значения модулей нормального ускорения и векторного произведения получим, что их модули равны , и направления совпадают. Тогда

. (3.20)

Таким образом, нормальное (центростремительное) ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора угловой скорости тела на вращательную скорость этой точки.