
- •Часть 1 теоретическая механика Учебное пособие
- •Предисловие
- •Введение
- •1. Задачи и методы теоретической механики
- •2. Основные понятия теоретической механики
- •3*. Из истории развития механики.
- •4.* История развития теоретической механики в России
- •5. Законы Ньютона
- •Введение в кинематику
- •2. Кинематика точки
- •2.1. Способы задания движения точки
- •2.1.1. Векторный способ задания движения
- •2.1.2. Координатный способ задания движения
- •2.1.3. Движение точки в декартовой системе координат
- •2.1.4. Естественный способ задания движения
- •П ри движении точки м расстояние с течением времени изменяется. Чтобы знать положение точки м на траектории в любой
- •Уравнение (2.4) выражает закон движения точки м вдоль траектории.
- •2. 2. Скорость точки
- •2.2.3. Скорость точки при естественном способе задания движения
- •2. 3. Ускорение точки
- •2.3.1. Ускорение точки при векторном способе задания движения.
- •2.3.2. Ускорение точки в декартовой системе координат
- •2.3.3. Естественные координатные оси. Вектор кривизны.
- •2.3.4. Ускорение точки при естественном способе задания движения
- •2.3.5. Классификация движения точки по ускорениям ее движения Рассмотрим зависимость характера движения точки от значений ее нормального и касательного ускорений.
- •Вопросы для повторения
- •3. Кинематика твердого тела
- •3.1. Общие положения
- •3. 2. Поступательное движение твердого тела
- •3.3. Вращение твердого тела вокруг неподвижной оси
- •3.3.1. Уравнение движения
- •3.3.2.Угловая скорость
- •3.3.3. Угловое ускорение
- •3.3.4. Равномерное и равнопеременное вращение
- •3.3.5. Скорости и ускорения точек вращающегося тела
- •3.3.6. Векторные выражения вращательной скорости, вращательного и центростремительного ускорений
- •3.3.7. Преобразование вращательного движения
- •Виды зацепления
- •Вопросы для повторения
2.3.4. Ускорение точки при естественном способе задания движения
Подставив вектор
скорости точки по формуле (2.11)
![]() в формулу ускорения
в формулу ускорения
![]() (2.14) и продифференцировав произведение
двух переменных величин по t,
получим:
(2.14) и продифференцировав произведение
двух переменных величин по t,
получим:
![]() ,
,
где
-
![]() ,
,
-
 .
.
А было неверно:
![]()
Тогда, подставив эти выражения в уравнение, получим:
![]() .
(2.24)
.
(2.24)
Произведя замену:
![]() ,
, ![]() ,
,
получим
![]() .
(2.25)
.
(2.25)
Таким образом, ускорение равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением точки (рис. 2.14). Модули этих ускорений соответственно равны
![]() ;
;
![]() .
(2.26)
.
(2.26)
Проекция вектора на бинормаль равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости.
Проекция ускорения точки на главную нормаль равна квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответствующей точке. Эта проекция всегда положительна! То есть нормальное ускорение точки всегда направлено к центру кривизны траектории и равно модулю этой проекции.
Проекция ускорения точки на касательную равна второй производной от дуговой координаты точки по времени или первой производной от алгебраической величины скорости точки по времени.
Модуль и направление полного ускорения определяется как
![]() ,
,
![]() ,
,
![]() ,
(2.27)
,
(2.27)
г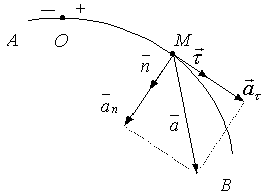 де
де
![]() и
и
![]() -
углы, образованные направлением
ускорения с принятыми направлениями
касательной и нормали в данной точке.
-
углы, образованные направлением
ускорения с принятыми направлениями
касательной и нормали в данной точке.
Если проекция
скорости
на касательную и
![]() имеют одинаковые знаки, то их направления
совпадают, то есть движение точки
имеют одинаковые знаки, то их направления
совпадают, то есть движение точки
Рис. 2.14 ускоренное.
Если же проекции
и
![]() на касательную имеют разные знаки, то
точка движется замедленно.
на касательную имеют разные знаки, то
точка движется замедленно.
При прямолинейном
движении точки радиус кривизны![]() ,
следовательно,
,
следовательно,
![]() .
.
Таким образом, нормальное ускорение существует лишь при криволинейном движении точки и характеризует изменение направления скорости.
При равномерном
движении v = const,
поэтому
![]() .
Следовательно, касательное ускорение
точки существует лишь при неравномерном
движении точки и характеризует
изменение модуля скорости.
.
Следовательно, касательное ускорение
точки существует лишь при неравномерном
движении точки и характеризует
изменение модуля скорости.
2.3.5. Классификация движения точки по ускорениям ее движения Рассмотрим зависимость характера движения точки от значений ее нормального и касательного ускорений.
Если
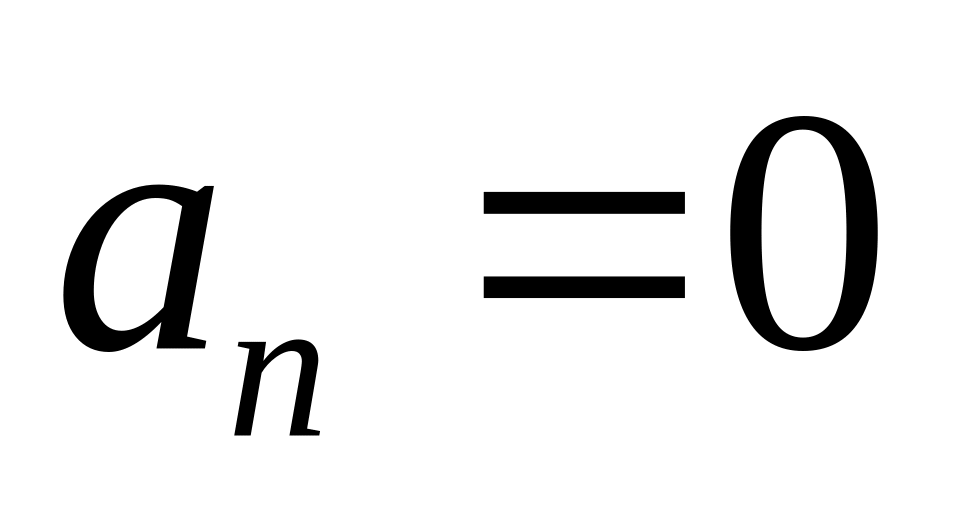 ,
,
 в начале некоторого промежутка времени,
то в течение этого времени не изменится
ни величина, ни модуль скорости, то есть
точка движется прямолинейно и равномерно.
в начале некоторого промежутка времени,
то в течение этого времени не изменится
ни величина, ни модуль скорости, то есть
точка движется прямолинейно и равномерно.
Если
 ,
во всем промежутке времени, то происходит
изменение направления скорости без
изменения ее модуля. При этом точка
движется криволинейно и равномерно,
а модуль ее ускорения
,
во всем промежутке времени, то происходит
изменение направления скорости без
изменения ее модуля. При этом точка
движется криволинейно и равномерно,
а модуль ее ускорения
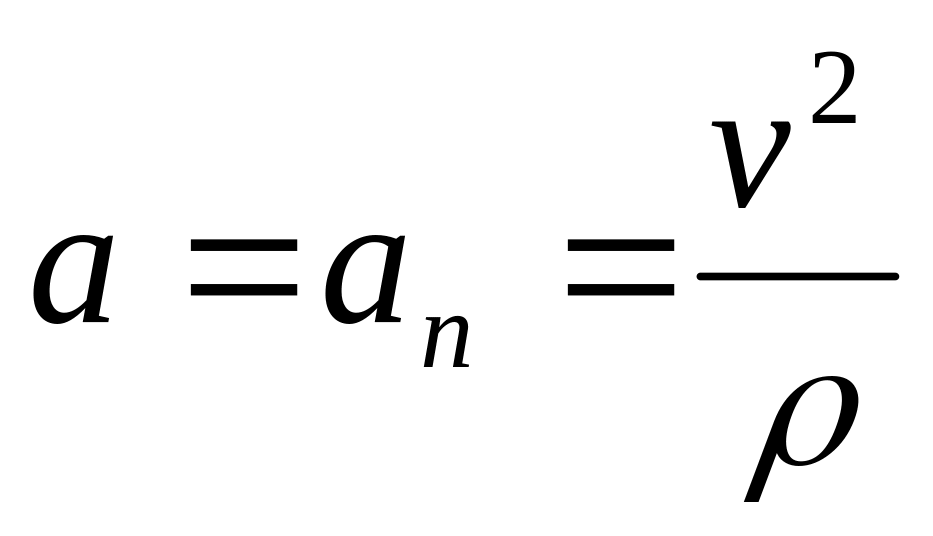 .
Если же
.
Если же
 в отдельный момент времени, то точка
движется неравномерно, и в этот момент
времени модуль ее скорости имеет
максимум, минимум или наименьшую
быстроту монотонного изменения.
в отдельный момент времени, то точка
движется неравномерно, и в этот момент
времени модуль ее скорости имеет
максимум, минимум или наименьшую
быстроту монотонного изменения.Если ,
 в течение некоторого промежутка времени,
то направление скорости не изменяется,
а изменяется ее модуль. То есть точка
движется прямолинейно неравномерно,
а модуль полного ускорения равен
в течение некоторого промежутка времени,
то направление скорости не изменяется,
а изменяется ее модуль. То есть точка
движется прямолинейно неравномерно,
а модуль полного ускорения равен
 .
При этом: если направления векторов
и
совпадают, то движение ускоренное, если
направления векторов
и
противоположны, то движение точки
замедленное. Если
в некоторый момент времени, то точка
движется не прямолинейно, а проходит
точку перегиба траектории, где
,
или модуль ее скорости обращается в
нуль (например, при изменении направления
движения точки
.
При этом: если направления векторов
и
совпадают, то движение ускоренное, если
направления векторов
и
противоположны, то движение точки
замедленное. Если
в некоторый момент времени, то точка
движется не прямолинейно, а проходит
точку перегиба траектории, где
,
или модуль ее скорости обращается в
нуль (например, при изменении направления
движения точки
 ).
).Если , в течение некоторого промежутка времени, то точка совершает криволинейное неравномерное движение, тогда модуль полного ускорения точки равен .
Если
 ,
то движение равнопеременное. Составим
уравнение равнопеременного движения
точки, полагая, что в начальный момент
t0 = 0, начальная
скорость точки равна v0,
а начальное значение дуговой координаты
S0.
,
то движение равнопеременное. Составим
уравнение равнопеременного движения
точки, полагая, что в начальный момент
t0 = 0, начальная
скорость точки равна v0,
а начальное значение дуговой координаты
S0.
В уравнении
![]() разделим переменные
разделим переменные
![]() .
Проинтегрируем полученное выражение
в указанных пределах
.
Проинтегрируем полученное выражение
в указанных пределах
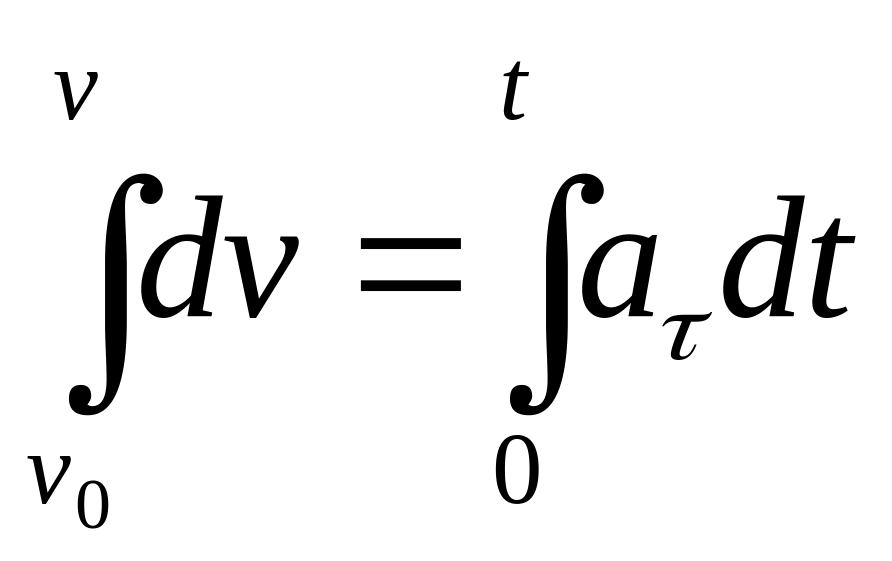 ,
тогда
,
тогда
![]() ,
или
,
или
![]() .
(2.28)
.
(2.28)
Выражение (2.28)
является формулой скорости
равнопеременного движения точки.
Преобразуем его к виду
![]() .
Разделив переменные, проинтегрируем
полученное уравнение в соответствующих
пределах:
.
Разделив переменные, проинтегрируем
полученное уравнение в соответствующих
пределах:
 ,
,
![]() ,
,
![]() .
(2.29)
.
(2.29)
Выражение (2.29) является уравнением равнопеременного движения. При ускоренном движении aτ > 0, а при замедленном aτ < 0.
2.3.6. Графики движения, пути, скорости и касательного ускорения точки
При движении точки по заданной траектории ее дуговая координата S, пройденный ею путь σ, скорость v и ускорение а меняются с течением времени, то есть они являются функциями времени, по которым можно построить в определенном масштабе графики, дающие наглядное представление о характере движения точки.
Г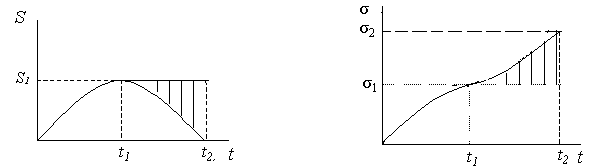 рафиком
движения точки называется график
зависимости ее дуговой координаты S от
времени t. График
движения, изображенный на рис. 2.15,
рафиком
движения точки называется график
зависимости ее дуговой координаты S от
времени t. График
движения, изображенный на рис. 2.15,
Рис. 2.15 Рис. 2.16
показывает, что в течение промежутка времени (0, t1) дуговая координата S возрастала от 0 до S1 то есть точка двигалась от начала отсчета в положительном направлении до точки с координатой S1, а затем в течение промежутка времени (t1, t2) дуговая координата убывала до нуля, то есть точка двигалась в обратном направлении до начала отсчета.
График пути можно построить по графику движения
Путь, пройденный точкой за некоторый промежуток времени представляет собой сумму абсолютных значений элементарных перемещений точки за данный промежуток времени. Графики движения и пути изображаются одной линией, если движение точки из начала отсчета происходит в положительном направлении (рис. 2.15 и 2.16), то есть в промежутке времени (0, t1) Путь, пройденный точкой к моменту t2 равен σ = 2S1.
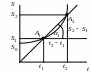
Пусть известен график движения точки (рис. 2.17). Определим алгебраическую величину средней скорости точки за промежуток (t1 ,t2) как
![]()
 ,
,
но
![]() .
.
Следовательно,
![]() то
то
есть средняя скорость точки
Рис. 2.17 за этот промежуток времени равна тангенсу угла наклона секущей А1А2 графика движения к оси времени t, а для некоторого момента времени скорость равна.
![]() .
.
Таким образом, для
определения скорости точки в данный
момент времени следует провести
касательную к графику движения в
соответствующей точке А (рис. 2.18) и
определить угол
![]() наклона этой касательной к оси времени
t. Тангенс угла α равен алгебраической
величине скорости точки в этот момент
времени.
наклона этой касательной к оси времени
t. Тангенс угла α равен алгебраической
величине скорости точки в этот момент
времени.
График скорости
(рис. 2.19) изображает зависимость
алгебраической величины скорости точки
![]() от времени t. Алгебраическая величина
касательного ускорения точки
от времени t. Алгебраическая величина
касательного ускорения точки
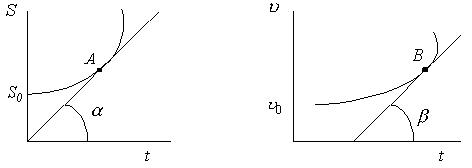 Рис.
2.18 Рис. 2.19
Рис.
2.18 Рис. 2.19
равна
![]() ,
т.е. для определения касательного
ускорения точки следует провести
касательную к графику скорости в
соответствующей точке В и найти
угол β наклона этой касательной к
оси t.
,
т.е. для определения касательного
ускорения точки следует провести
касательную к графику скорости в
соответствующей точке В и найти
угол β наклона этой касательной к
оси t.
 Тангенс угла β
определяет алгебраическую величину
касательного ускорения.
Тангенс угла β
определяет алгебраическую величину
касательного ускорения.
График касательного ускорения (рис.2.19) изображает зависимость алгебраической величины касательного ускорения aτ от времени t.
Рис. 2.20
