2.2.3. Скорость точки при естественном способе задания движения

Пусть в момент точка занимала положение М, а в момент – положение М₁ (рис. 2.9). Дуговые координаты этих точек будут соответственно равны:

; ,

г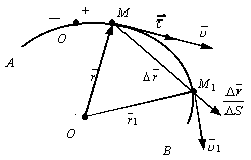 де .

Проведем из произвольного центра О, радиус – вектор . Тогда по формуле (2.7)

.

Рис. 2.9 Введем в это выражение , тогда

.

Здесь вектор и направлен также как вектор . При ΔS→0 его направление стремиться к направлению касательной, проведенной в точке М в сторону увеличения дуговой координаты. А модуль стремится к 1, то есть вектор направлен по касательной к кривой в сторону увеличения дуговой координаты и по модулю равен единице. Обозначим его ортом . Тогда:

, (2.11)

где – скалярная величина, представляющая собой проекцию вектора скорости точки на касательную к ее траектории и называется алгебраической скоростью точки.

. (2.12)

То есть модуль скорости равен абсолютному значению производной от дуговой координаты по времени.

Знак скорости v указывает направление движения точки по траектории. Если

1. , то функция S(t) убывает и направление скорости противоположно направлению касательного орта .

2. , то функция S(t) возрастает, то есть точка движется в сторону возрастания дуговой координаты S(t) и направление скорости совпадает с направлением касательного орта .

3. и изменяет знак, то дуговая координата S(t) в этот момент времени достигает максимального или минимального значения, а точка меняет свое направление движения.

2. 3. Ускорение точки

2.3.1. Ускорение точки при векторном способе задания движения.

Ускорение при криволинейном движении характеризует изменение модуля и направления скорости точки с течением времени.

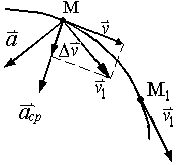
Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость , а в момент приходит в положение М₁ и имеет скорость (рис. 2.10). Тогда за промежуток времени скорость получает приращение .

Для построения вектора отложим от точки М вектор и построим параллелограмм, в котором диагональю будет , тогда вторая сторона параллелограмма изображает вектор . Заметим, что вектор всегда направлен в сторону вогнутости кривой.

Отношение приращения вектора скорости к соответствующему промежутку времени определяет вектор среднего ускорения точки за этот промежуток времени:

. (2.13)

Вектор среднего ускорения, очевидно, имеет тоже направление, что и вектор , т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени

называется векторная величина , к которой стремится среднее ускорение при стремлении Δt→0,

,

или

(2.14) Следовательно, вектор ускорения точки в данный момент времени

Рис. 2.10 равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.

Если траектория точки плоская кривая, то вектор ускорения лежит в плоскости этой кривой и направлен в сторону вогнутости.

Е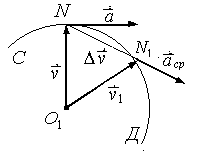 сли траектория точки – пространственная кривая, то вектор направлен в сторону вогнутости кривой. Вектор расположен в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке М₁. В пределе, когда точка М₁ стремиться к точке М, эта плоскость занимает положение так называемой соприкасающейся плоскости, следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Другой способ. Построив годограф скорости СД (рис. 2.11), отложим там скорости и , приращения скорости , а также вектор

Рис. 2.11 среднего ускорения , направленного по хорде NN₁ годографа скорости. Предел, к которому стремится вектор среднего ускорения точки в данный момент времени t равен:

,

а так как скорость является вектором функции от времени, то есть , а ,

то выражение ускорения имеет тот же вид, что и (2.14):

.