2.3.2. Ускорение точки в декартовой системе координат

В Декартовой системе координат вектор ускорения точки равен

. (2.15).

В то же время.

(2.16)

С равнивая правые части этих уравнений, видим, что

;

; . (2.17)

Таким образом, проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствующих координат точки по времени или первым производным по времени от проекций скорости на соответствующие оси.

Уравнения (2.17) являются уравнениями годографа вектора ускорения в параметрическом виде. Чтобы получить уравнение годографа в явном виде, необходимо из уравнений исключить параметр t. Модуль и направление ускорения можно определить по формулам:

, (2.18) ; ; , (2.19)

где α, β, γ – углы между вектором скорости и осями координат

2.3.3. Естественные координатные оси. Вектор кривизны.

Проведем через точку М три плоскости (рис.2.12):

- касательную;

- соприкасающуюся (плоскость предельное положение которой проходит через касательную в точке М и прямую, параллельную касательной в точке М₁ при стремлении М₁→М);

- плоскость, перпендикулярную касательной, называемой нормальной плоскостью.

Линия пересечения соприкасающейся и нормальной плоскости называется главной нормалью кривой.

Нормаль, перпендикулярная главной нормали, называется бинормалью.

Естественными координатными осями называются три взаимно перпендикулярные оси (рис.2.12):

1. касательная, направленная в сторону возрастания дуговой координаты;

2. главная нормаль, направленная в сторону вогнутости кривой;

3. бинормаль, направленная по отношению к нормали и касательной так же, как и ось Oz ориентирована по отношению к осям Ox, Oy декартовой системы координат.

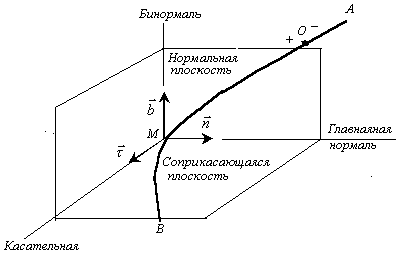
Рис. 2.12

Единичные векторы – орты этих осей обозначают соответственно , и .

Естественные координатные оси имеют начало в точке М кривой и при движении точки М по этой кривой перемещаются вместе с ней, оставаясь взаимно перпендикулярными, но изменяя свое положение в пространстве. Эти оси - подвижные.

Возьмем на кривой АВ две точки М и М₁ (рис. 2.13). Соответствующим дуговым координатам , . Покажем орты касательной и в этих точках. Модуль орта постоянен, а направление орта изменится при перемещении точки, следовательно, орт является переменным вектором. Приращение орта на участке равно стороне параллелограмма, построенного со стороной и диагональю . Отношение характеризует поворот касательной на у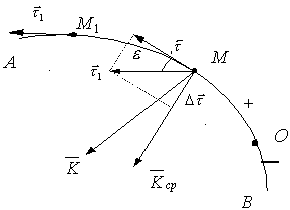 частке ММ₁ и называется вектором средней кривизны кривой на участке ММ₁. Этот вектор имеет направление вектора и направлен в сторону вогнутости кривой.

Рис. 2.13 (2.20)

П редел, к которому стремится вектор средней кривизны кривой , когда ΔS→0, называется вектором кривизны траектории в данной точке.

,

а , следовательно

. (2.21)

Следовательно, вектор кривизны кривой в данной точке равен производной от орта касательной к кривой по дуговой координате.

Определим модуль этого вектора.

Угол между направлениями касательных в двух точках кривой и называется углом смежности .

При малых расстояниях угол смежности тоже мал. Модуль определим как сторону основания равнобедренного треугольника, образованного ортами , и с малым углом ε при вершине и боковыми сторонами, равными единице.

.

Модуль вектора определяется как . Из дифференциальной геометрии известно, что предел отношения угла смежности ε к приращению дуговой координаты при ΔS→0 равен кривизне кривой , где ρ – радиус кривизны кривой в точке М и вектор находится в соприкасающейся плоскости.

Учитывая выше сказанное, получим:

. (2.22)

Так как вектор кривизны находится в соприкасающейся плоскости и перпендикулярен орту , то он направлен по главной нормали к центру кривизны кривой.

. (2.23)