Лекция 14. Векторные свойства временных разверток План

1. Линейность временных разверток

2. Характеристики множества обобщеных временных разверток

3. Свойства временных разверток при фиксированном векторе задержек

1. Линейность временных разверток

Пусть задан вектор задержек . Для того, чтобы вектор был вектором временной развертки, соответствующим вектору , необходимо и достаточно, чтобы при наличии дуги в графе алгоритма выполнялось:

- . (1)

Утверждение 1. Пусть векторы , являются временными развертками соответственно для векторов задержек . Тогда:

• Вектор + является временной разверткой для вектора задержек ;

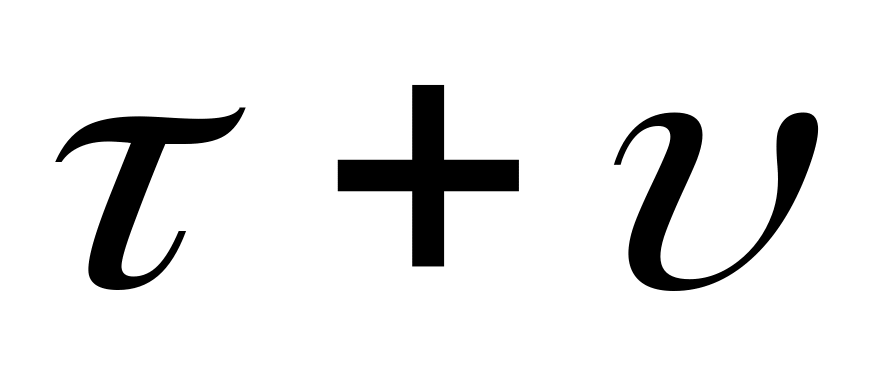• Для любого 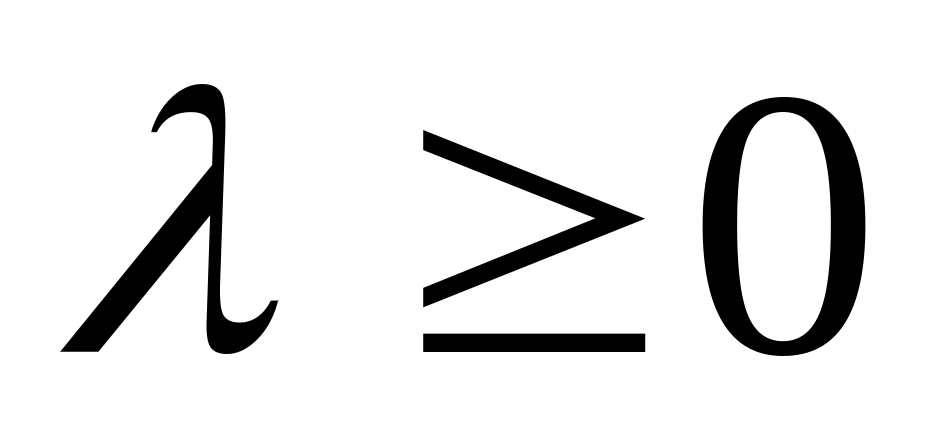вектор 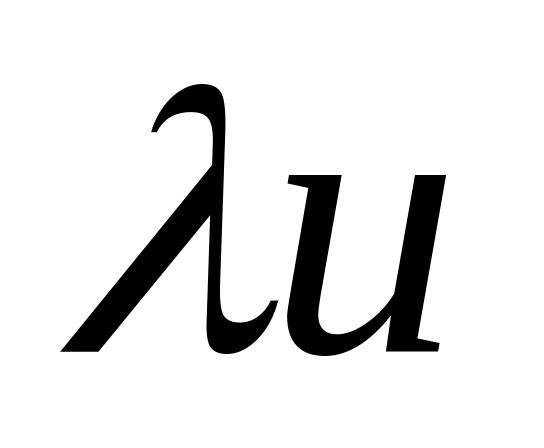является временной разверткой для вектора задержек .

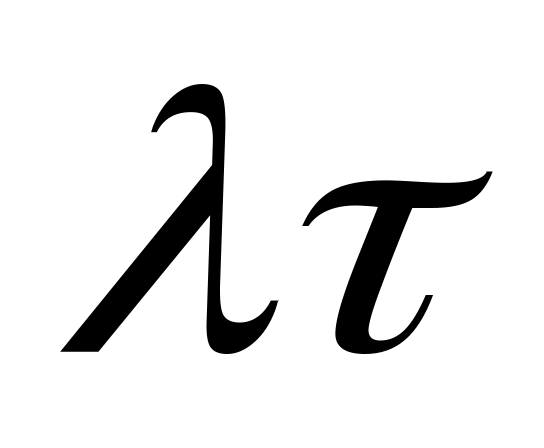Для пар векторов , и , выполняются соотношения (1): - , - . Поэтому

- ;

,

т.е. для векторов + и также выполняются соотношения (1).

2. Характеристики множества обобщеных временных разверток

Утверждение 2. Множество обобщеных временных разверток является линейным конусом.

Действительно, пусть векторы , являются обобщенными временными развертками. Согласно (1), это означает:

- , - (2)

для всех подходящих пар индексов. В соответствии с предыдущим утверждением аналогичные (2) неравенства будут выполняться и для координат векторов + и для любого . Следовательно, векторы + и также являются обощеными временными развертками, а все множество - линейным конусом.

Следствие. Множество обобщеных временных разверток выпукло и замкнуто.

Множество называется выпуклым, если вместе с любыми элементами , , принадлежащими этому множеству, ему принадлежит также , где .

Пусть векторы , являются обобщенными временными развертками, тогда выполняется (2). Поэтому для любого имеем:

,

Т.е. вектор .

Множество называется замкнутым, если содержит все свои предельные точки.

Пусть вектор - предельная точка для множества . Тогда существует последовательность обобщенных временных разверток , сходящаяся к . Тогда

,

т.е. вектор .

Множество обобщеных временных разверток оказалось конусом только потому, что оно соответствует нулевому вектору задержек. Если вектор является временной разверткой с вектором задержек , то он будет оставаться временной разверткой для всех неотрицательных векторов задержек, у которых координаты не превосходят соответствующих координат вектора . Это следует из того, что неравенство (1) остаются в силе при уменьшении .

3. Свойства временных разверток при фиксированном векторе задержек

Утверждение 3. При фиксированном векторе задержек множество временных разверток обладает следующими свойствами:

• Сумма временных разверток является временной разверткой;

• Произведение временной развертки на число 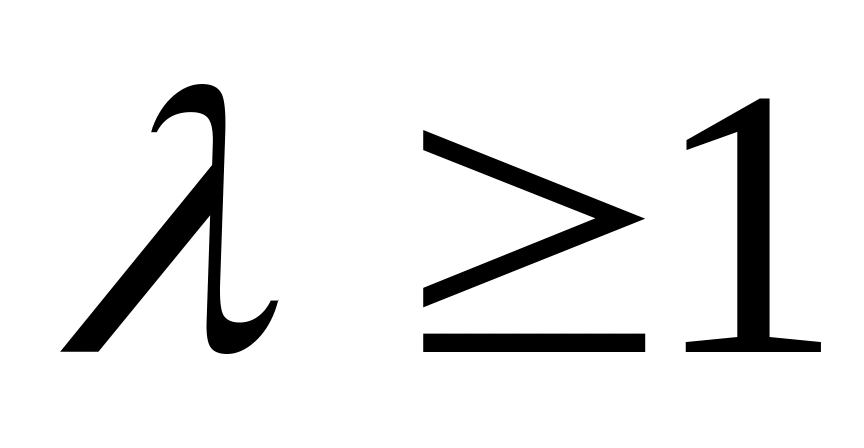является временной разверткой;

• множество временных разверток выпукло и замкнуто.

Пусть векторы , являются временными развертками для вектора задержек . Тогда:

- ,

Следовательно + .

,

Следовательно .

Для любого имеем:

,

Т.е. вектор , - выпукло.

При фиксированном ненулевом векторе задержек множество временных разверток не является конусом. Однако при любом развертки из входят во множество . Несмотря на то, что множество содержит в себе все множества , само оно, в свою очередь, содержится в некотором смысле в каждом .

Утверждение 4. Пусть - какая-нибудь фиксированная временная развертка из . Тогда для любой обобщенной временной развертки вектор .

Действительно: - , - для всех подходящих пар . Тогда

- .

Таким образом, конус обобщенных временных разверток , сдвинутый параллельно на любую развертку из , содержится в при любом .

Надо выяснить, когда множества и совпадают с точностью до параллельного переноса.

Утверждение 5. Пусть СЛАУ

- (3)

совместна и вектор является ее решением. Тогда множества и совпадают с точностью до параллельного переноса на вектор .

Действительно, . Тогда в силу утверждения 4, множество , сдвинутое на вектор , содержится в . Остается показать, что любую развертку из можно представить, как некоторую обобщенную развертку из , сдвинутую на вектор . Пусть - произвольная развертка из , . Рассмотрим вектор . Имеем - . Вычитая отсюда (3), получим - , т.е. .

Совместимость (3) дает достаточное условие совпадения и . Какие необходимые условия? Предположим, что множество получается из множества с помощью параллельного переноса на вектор . Чем характерна временная развертка ?

Какова бы ни была развертка , она получается как сумма развертки из и , тогда вектор является обобщенной временной разверткой. Пусть дуга идет из в . Т.к. - замкнутое, то при фиксированных и существует развертка, на которой величина - достигает в своего минимального значения. В силу того, что вектор является обобщенной временной разверткой, выполняется - . Отсюда вытекает . Это означает, что имеет место

Утверждение 6. Пусть множество получается из множества с помощью параллельного переноса на вектор . Тогда для любых пар , , соответствующих дугам графа алгоритма, минимальное значение - для всех разверток равно - .

Таким образом, координаты развертки обеспечивают наилучшее удовлетворение неравенств (1), максимально приближая каждое из них к равенству. При совместимости СЛАУ (3) все неравенства (1) становятся на развертке равенствами.

Вопросы

1. Сформулировать критерий того, что вектор является вектором временной развертки, соответствующим вектору .

2. Как связана временная развертка для суммы векторов задержек с временными развертками слагаемых? Показать.

3. Как связана временная развертка для для вектора задержек с временной разверткой для вектора задержек ? Показать.

4. Показать, что множество обобщеных временных разверток является линейным конусом.

5. Показать, что множество обобщеных временных разверток выпукло и замкнуто.

6. Свойства множества временных разверток при фиксированном векторе задержек. Доказать.

Литература

1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с.

2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с.

3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с.

4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с.

5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с.

6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.