Свойства вершин ориентированного ациклического графа
Свойства топологической сортировки графа
Топологические уровни графа алгоритма
1. Свойства вершин ориентированного ациклического графа
Одно из основных направлений исследования структуры алгоритма связано с выявлением возможностей параллельного, т.е. одновременного выполнения операций алгоритма [Воеводин]. Основная идея такого исследования заключается в следующем. Любая реализация алгоритма – это протекающий во времени процесс. Если конкретная реализация фиксирована, то в каждый момент времени можно сказать, какие из операций алгоритма выполняются одновременно. Всякая операция, выполняемая в данный момент, могла получить свои аргументы только от операций, выполнение которых закончилось раньше. Поэтому любая реализация алгоритма должна порождать вполне определенную сортировку его операций. Эта сортировка представляет из себя выделение групп операций, обладающих следующими свойствами:
группы выполняются последовательно друг за другом,
операции внутри каждой группы могут выполняться параллельно (одновременно).
О структуре алгоритма пока ничего не известно, кроме того, что сам алгоритм может быть описан ориентированным ациклическим графом. Во всяком процессе реализации алгоритма есть его начало и конец. Начало в графе алгоритма отождествляется с вершиной, не имеющей входящих ребер, конец – с вершиной, не имеющей выходящих ребер.
Утверждение 111. В любом ориентированном ациклическом графе существует хотя бы одна вершина, не имеющая входящих дуг, и хотя бы одна вершина, не имеющая выходящих дуг [Харари].
Доказательство. Если граф пустой (не имеет ребер), то утверждение очевидно. Пусть в графе есть хоть одно ребро. Рассмотрим какой-нибудь критический путь графа. Предположим, что его первая по порядку вершина имеет входящую дугу. Возможна одна из двух ситуаций:
1. Предшествующая вершина совпадает с одной из вершин, образующих критический путь, но тогда граф будет содержать цикл, что противоречит его ацикличности;
2. Предшествующая вершина не совпадает ни с одной из вершин, образующих критический путь, но тогда существует путь, имеющий бóльшую длину, чем критический. Вновь получено противоречие.
Таким образом, первая по порядку вершина критического пути не может иметь входящих ребер.
Аналогично строится доказательство для выходящей вершины.
2. Свойства топологической сортировки графа
Утверждение 111 показывает, что вершины графа любого алгоритма можно разбить, по крайней мере, на три группы. Первая группа содержит не менее одной входной вершины, третья – не менее одной выходной вершины. Вторая группа – все остальные вершины. Соответствующие группы операций алгоритма могут быть выполнены последовательно друг за другом. Наибольший интерес с точки зрения анализа алгоритма вызывает вторая группа.
Утверждение
123.
Пусть задан ориентированный ациклический
граф, имеющий
вершин. Существует натуральное число
,
для которого все вершины графа можно
так пометить одним из индексов
,
что если дуга идет из вершины с индексом
в вершину с индексом
,
то
[Воев].
Доказательство. Выберем в графе любое число входных вершин и пометим их индексом 1. Удалим из графа помеченные вершины и инцидентные им ребра. Оставшийся граф также ориентированный и ациклический. Выберем в нем любое число входных вершин (в соответствии с утверждением 111 хотя бы одна такая вершина есть) и пометим их индексом 2. Снова удалим помеченные вершины и инцидентные им ребра. Продолжим этот процесс, пока не исчерпаем весь граф. Так как при каждом помечивании помечается не менее одной вершины, то число различных индексов не превышает числа вершин.
Следствие 1. Никакие две вершины с одинаковыми индексами не являются смежными.
Следствие 2. Минимальное число индексов, которыми можно пометить все вершины графа, на 1 больше длины его критического пути.
Следствие
3.
Для любого натурального числа
,
большего длины критического пути,
существует такая разметка вершин графа,
при которой используются все
индексов.
Разметка вершин графа, проведенная в соответствии с утверждением 123, называется топологической сортировкой, а вершины, помеченные одним индексом, образуют топологический уровень.
Если при топологической сортировке графа некоторая вершина помечена индексом , то длина всех путей, оканчивающихся в этой вершине, меньше .
Пример.
Построить топологическую сортировку
графа
(рис.9.1(а)). На рис.9.1(б-к) отражены
последовательные шаги построения
сортировки в соответствии с доказательством
утверждения 123. В результате получено
разбиение множества вершин графа на
следующие топологические уровни:
-
Номер топологического уровня
Вершины графа
1
1, 2
2
3, 4, 5
3
6, 8
4
7, 10
5
9
6
11
7
13
8
12
9
14, 15
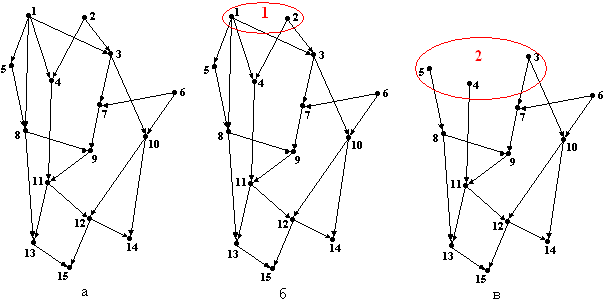
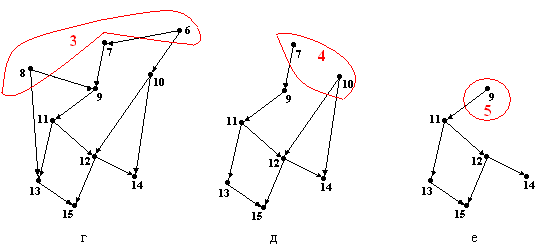
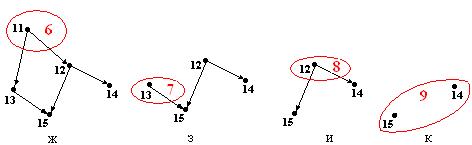
Рис.9.1. Исходный граф (а), последовательные шаги построения топологической сортировки (б-к)
Если на каждом шаге построения топологической сортировки помечать все возможные вершины, то количество уровней будет минимальным и равным 7 (рис.9.2) (сравнить с длиной критического пути графа, которая равна 6), при этом разбиение множества вершин графа на топологические уровни будет иметь следующий вид:
-
Номер топологического уровня
Вершины графа
1
1, 2, 6
2
3, 4, 5
3
7, 8, 10
4
9
5
11
6
12, 13
7
14, 15
Таким образом, каждому графу может соответствовать множество различных топологических сортировок.
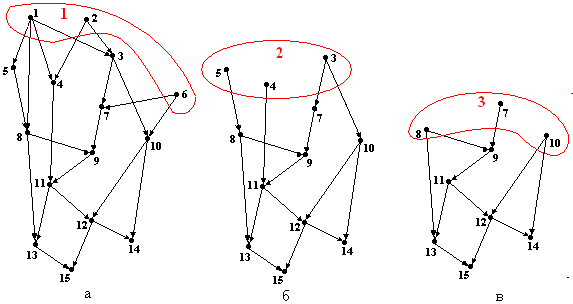
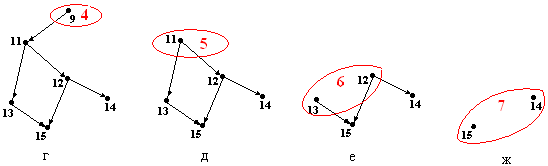
рис.9.2. Топологическая сортировка графа, содержащая минимальное количество уровней
Замечание
1000.
Утверждение 123 остается в силе, если
неравенство
заменить неравенством
,
однако ни одно из следствий уже выполняться
не будет. Такая разметка вершин графа
называется обобщенной
топологической сортировкой.
Обобщенная топологическая сортировка является удобным промежуточным объектом в процессе отыскания нужной топологической сортировки. Если найдена нетривиальная обобщенная топологическая сортировка, то для нахождения топологической сортировки не обязательно снова рассматривать весь граф. Довольно часто могут быть получены хорошие результаты, если отыскать подходящие топологические сортировки для подграфов, определяемых группами вершин обобщенной топологической сортировки, и из них составить топологическую сортировку исходного графа, используя предложенный ниже алгоритм построения топологической сортировки объединения графов Ниже обязательно привести пример.
Топологическая сортировка называется линейной, если индексы любых вершин различны. В этом случае говорят, что граф линейно упорядочен. Если топологическая сортировка (или обощенная топологическая сортировка) не являются линейными, то из нее легко получить другие сортировки с бóльшим числом индексов.