
- •2. Общие требования к алгоритму
- •3. Формальное представление алгоритма. Машина Тьюринга
- •4. Алгоритмически неразрешимые проблемы: их существование и примеры
- •Вопросы
- •2. Теория возмущений и числа обусловленности задачи
- •3. Влияние ошибок округления на алгоритмы
- •4. Программирование численных алгоритмов
- •Вопросы
- •Основные характеристики алгоритма при его анализе. Вычислительная сложность алгоритма
- •Классы входных данных
- •Сложность алгоритма по памяти
- •2. Классы входных данных
- •3. Сложность алгоритма по памяти
- •Вопросы
- •Лекция 4. Оценка вычислительной сложности алгоритма План
- •Предварительные шаги для оценки вычислительной сложности алгоритма
- •Скорость роста алгоритма
- •Анализ подходов, связанных с поиском информации
- •1. Предварительные шаги для оценки вычислительной сложности алгоритма
- •2. Скорость роста алгоритма
- •3. Анализ подходов, связанных с поиском информации
- •Вопросы
- •Класс р - задачи с полиномиальной сложностью
- •Класс np - полиномиально проверяемые задачи
- •1. Класс р - задачи с полиномиальной сложностью
- •2. Класс np - полиномиально проверяемые задачи
- •Вопросы
- •Лекция 6. Сложностные классы задач (продолжение) План
- •Приближенные методы решения np-задач
- •2. Приближенные методы решения np-задач
- •Вопросы
- •Лекция 7. Численные алгоритмы План
- •Вычисление значений многочлена
- •Решение системы линейных алгебраических уравнений
- •1. Вычисление значений многочлена
- •2. Решение системы линейных алгебраических уравнений
- •Вопросы
- •Цели анализа последовательных алгоритмов
- •Основы построения графа алгоритма
- •Допустимые преобразования алгоритма
- •2. Основы построения графа алгоритма
- •Последовательность операций
- •3. Допустимые преобразования алгоритма
- •Вопросы
- •Свойства вершин ориентированного ациклического графа
- •Свойства топологической сортировки графа
- •Топологические уровни графа алгоритма
- •1. Свойства вершин ориентированного ациклического графа
- •2. Свойства топологической сортировки графа
- •3. Топологические уровни графа алгоритма
- •Вопросы
- •Лекция 10. Топологические сортировки сложных графов План
- •Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
- •Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиения
- •1. Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
- •2. Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиения
- •Вопросы
- •Операция элементарного гомоморфизма
- •Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки
- •Использование гомоморфной свертки для упрощения процесса исследования структуры алгоритма
- •1. Операция элементарного гомоморфизма
- •2. Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки
- •3. Использование гомоморфной свертки для упрощения процесса исследования структуры алгоритма
- •Вопросы
- •Лекция 12. Внутренний параллелизм алгоритма План
- •Понятие внутреннего параллелизма алгоритма и его использование
- •О выборе расположения вершин графа алгоритма
- •Особенности алгоритма решения системы линейных алгебраических уравнений
- •1. Понятие внутреннего параллелизма алгоритма и его использование
- •2. О выборе расположения вершин графа алгоритма
- •3. Особенности алгоритма решения системы линейных алгебраических уравнений
- •Вопросы
- •Лекция 13. Временные развертки План
- •Основная проблема анализа алгоритма с использованием соответствующего графа
- •Вектор временной развертки, обобщенной временной развертки
- •Время реализации алгоритма
- •1. Основная проблема анализа алгоритма с использованием соответствующего графа
- •2. Вектор временной развертки, обобщенной временной развертки
- •3. Время реализации алгоритма
- •Вопросы
- •Лекция 14. Векторные свойства временных разверток План
- •Линейность временных разверток
- •Характеристики множества обобщеных временных разверток
- •Свойства временных разверток при фиксированном векторе задержек
- •1. Линейность временных разверток
- •2. Характеристики множества обобщеных временных разверток
- •3. Свойства временных разверток при фиксированном векторе задержек
- •Лекция 15. Векторные свойства временных разверток (продолжение) План
- •Ориентированная задержка цикла. Уравновешенный цикл.
- •Пространственно-временные развертки
- •1. Ориентированная задержка цикла. Уравновешенный цикл
- •2. Условие совпадения множеств и с точностью до параллельного переноса
- •3. Пространственно-временные развертки.
Вопросы
Когда возникает семейство «похожих» алгоритмов?
Всегда ли можно точно построить граф алгоритма, содержащего условные операции? Почему?
Можно ли по имеющейся топологической сортировке графа получить топологические сортировки его подграфов? Как это сделать? Когда возникает такая необходимость? Привести пример.
Что назыв ется множеством теряемых ребер графа, когда это множество возникает? Привести примеры.
Какие вершины графа называются граничными вершинами? Привести примеры.
Написать программу, реализующую алгоритм построения топологической сортировки объединения двух графов по имеющимся топологическим сортировкам этих графов.
Литература
Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с.
Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с.
Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с.
Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с.
Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с.
Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
Кобозева А.А., Нариманова Е.В. Метод построения топологической сортировки объединения графов, используемый при распараллеливании последовательных алгоритмов / Труды Одесского политехнического университета. – 2006. - №2(26). - С. 156-161.
Лекция 11. Использование операций гомоморфизма при построении топологических сортировок графов
План
Операция элементарного гомоморфизма
Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки
Использование гомоморфной свертки для упрощения процесса исследования структуры алгоритма
1. Операция элементарного гомоморфизма
Предположим, что для некоторого графа по каким-то причинам вызывает трудности отыскание топологической сортировки с нужными свойствами. Допустим, что прибавляя к этому графу вершины и дуги, можно получить граф, для которого нужная сортировка находится легко. Тогда она может породить требуемую сортировку и для исходного графа.
Заметим, что сам процесс расширения графа можно осуществить в разные моменты времени. Это можно явно делать после построения графа алгоритма. Но можно делать и неявно до построения графа алгоритма, изменяя форму записи алгоритма таким образом, чтобы гарантировать, что полученный в результате этого изменения граф будет расширенным по отношению к исходному.
 Кроме
расширения графа можно также использовать
его сужение,хотя
не каждое сужение будет давать хорошие
результаты. Однако один тип сужения
оказывается очень эффективным.
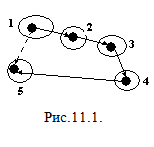
Предположим, что концы некоторой дуги
связаны еще каким-то путем. Если мы
исключим из графа эту дугу, то очевидно,
что множества топологических сортировок
исходного и полученного графа будут
полностью совпадать (рис.11.1).
Кроме
расширения графа можно также использовать
его сужение,хотя
не каждое сужение будет давать хорошие
результаты. Однако один тип сужения
оказывается очень эффективным.
Предположим, что концы некоторой дуги
связаны еще каким-то путем. Если мы
исключим из графа эту дугу, то очевидно,
что множества топологических сортировок
исходного и полученного графа будут
полностью совпадать (рис.11.1).
Для исследования топологических сортировок полезным оказывается сужение, основанное на операциях гомоморфизма.
Для упрощения исследования топологических сортировок графа информационного процесса полезным оказывается модификация, основанная на операциях гомоморфизма.
Пусть
дан ориентированный граф
![]() ;
;
![]() —
произвольные две вершины графа;
—
произвольные две вершины графа;
![]() .
Две вершины
.
Две вершины
![]() заменяются одной новой вершиной
.
Пусть
заменяются одной новой вершиной
.
Пусть
![]() .
Изменим множество ребер
исходного графа, результатом чего будет
.
Изменим множество ребер
исходного графа, результатом чего будет
![]() ,
следующим образом: если очередное ребро
в
не инцидентно ни одной из вершин
,
то это ребро просто переносится в
;
в противном случае ребро в
получается из ребра в
заменой вершин
новой вершиной
.
В этом случае говорят, что граф
,
следующим образом: если очередное ребро
в
не инцидентно ни одной из вершин
,
то это ребро просто переносится в
;
в противном случае ребро в
получается из ребра в
заменой вершин
новой вершиной
.
В этом случае говорят, что граф
![]() получается из графа
с помощью операции элементарного
гомоморфизма.
Операция элементарного гомоморфизма
может привести к появлению циклов,
кратных дуг, даже если исходный граф их
не имел (рис.11.2). Если после описанной
операции исключаются все петли, а все
кратные дуги отождествляются, то такая
операция называется простым
элементарным гомоморфизмом,
в противном случае —
кратным
элементарным гомоморфизмом
или элементарным
гомоморфизмом.
получается из графа
с помощью операции элементарного
гомоморфизма.
Операция элементарного гомоморфизма
может привести к появлению циклов,
кратных дуг, даже если исходный граф их
не имел (рис.11.2). Если после описанной
операции исключаются все петли, а все
кратные дуги отождествляются, то такая
операция называется простым
элементарным гомоморфизмом,
в противном случае —
кратным
элементарным гомоморфизмом
или элементарным
гомоморфизмом.
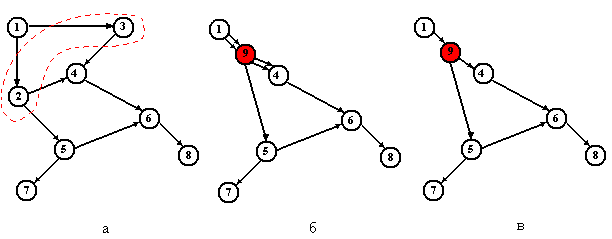
Рис.11.2. Исходный граф (а); результат кратного элементарного гомоморфизма вершин 2 и 3 (б); результат простого элементарного гомоморфизма (в)
