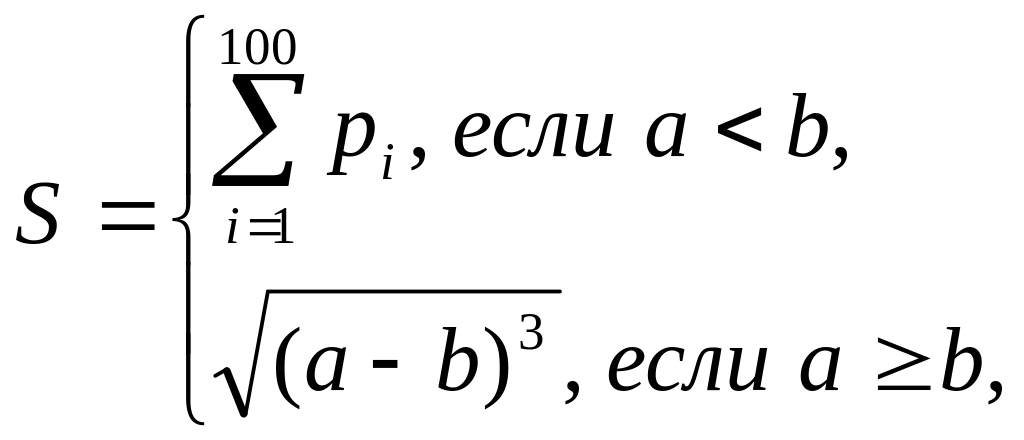- •2. Общие требования к алгоритму
- •3. Формальное представление алгоритма. Машина Тьюринга
- •4. Алгоритмически неразрешимые проблемы: их существование и примеры
- •Вопросы
- •2. Теория возмущений и числа обусловленности задачи
- •3. Влияние ошибок округления на алгоритмы
- •4. Программирование численных алгоритмов
- •Вопросы
- •Основные характеристики алгоритма при его анализе. Вычислительная сложность алгоритма
- •Классы входных данных
- •Сложность алгоритма по памяти
- •2. Классы входных данных
- •3. Сложность алгоритма по памяти
- •Вопросы
- •Лекция 4. Оценка вычислительной сложности алгоритма План
- •Предварительные шаги для оценки вычислительной сложности алгоритма
- •Скорость роста алгоритма
- •Анализ подходов, связанных с поиском информации
- •1. Предварительные шаги для оценки вычислительной сложности алгоритма
- •2. Скорость роста алгоритма
- •3. Анализ подходов, связанных с поиском информации
- •Вопросы
- •Класс р - задачи с полиномиальной сложностью
- •Класс np - полиномиально проверяемые задачи
- •1. Класс р - задачи с полиномиальной сложностью
- •2. Класс np - полиномиально проверяемые задачи
- •Вопросы
- •Лекция 6. Сложностные классы задач (продолжение) План
- •Приближенные методы решения np-задач
- •2. Приближенные методы решения np-задач
- •Вопросы
- •Лекция 7. Численные алгоритмы План
- •Вычисление значений многочлена
- •Решение системы линейных алгебраических уравнений
- •1. Вычисление значений многочлена
- •2. Решение системы линейных алгебраических уравнений
- •Вопросы
- •Цели анализа последовательных алгоритмов
- •Основы построения графа алгоритма
- •Допустимые преобразования алгоритма
- •2. Основы построения графа алгоритма
- •Последовательность операций
- •3. Допустимые преобразования алгоритма
- •Вопросы
- •Свойства вершин ориентированного ациклического графа
- •Свойства топологической сортировки графа
- •Топологические уровни графа алгоритма
- •1. Свойства вершин ориентированного ациклического графа
- •2. Свойства топологической сортировки графа
- •3. Топологические уровни графа алгоритма
- •Вопросы
- •Лекция 10. Топологические сортировки сложных графов План
- •Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
- •Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиения
- •1. Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
- •2. Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиения
- •Вопросы
- •Операция элементарного гомоморфизма
- •Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки
- •Использование гомоморфной свертки для упрощения процесса исследования структуры алгоритма
- •1. Операция элементарного гомоморфизма
- •2. Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки
- •3. Использование гомоморфной свертки для упрощения процесса исследования структуры алгоритма
- •Вопросы
- •Лекция 12. Внутренний параллелизм алгоритма План
- •Понятие внутреннего параллелизма алгоритма и его использование
- •О выборе расположения вершин графа алгоритма
- •Особенности алгоритма решения системы линейных алгебраических уравнений
- •1. Понятие внутреннего параллелизма алгоритма и его использование
- •2. О выборе расположения вершин графа алгоритма
- •3. Особенности алгоритма решения системы линейных алгебраических уравнений
- •Вопросы
- •Лекция 13. Временные развертки План
- •Основная проблема анализа алгоритма с использованием соответствующего графа
- •Вектор временной развертки, обобщенной временной развертки
- •Время реализации алгоритма
- •1. Основная проблема анализа алгоритма с использованием соответствующего графа
- •2. Вектор временной развертки, обобщенной временной развертки
- •3. Время реализации алгоритма
- •Вопросы
- •Лекция 14. Векторные свойства временных разверток План
- •Линейность временных разверток
- •Характеристики множества обобщеных временных разверток
- •Свойства временных разверток при фиксированном векторе задержек
- •1. Линейность временных разверток
- •2. Характеристики множества обобщеных временных разверток
- •3. Свойства временных разверток при фиксированном векторе задержек
- •Лекция 15. Векторные свойства временных разверток (продолжение) План
- •Ориентированная задержка цикла. Уравновешенный цикл.
- •Пространственно-временные развертки
- •1. Ориентированная задержка цикла. Уравновешенный цикл
- •2. Условие совпадения множеств и с точностью до параллельного переноса
- •3. Пространственно-временные развертки.
Лекция 10. Топологические сортировки сложных графов План
Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиения
1. Особенности и рекомендации построения топологических сортировок графов алгоритмов, содержащих условные операции
Граф алгоритма определяется однозначно по его записи только для фиксированных входных данных. Если в записи алгоритма имеются условные операции, то такую запись надо считать записью семейства «похожих» алгоритмов [Воев]. В свою очередь подобная запись порождает семейство «похожих» графов. Для конкретных входных данных можно даже не знать, с каким конкретно графом из семейства «похожих» графов приходится иметь дело. Такая ситуация возникает, если условные операции зависят от входных данных достаточно сложно, например, определяются результатами промежуточных вычислений. Вместо того, чтобы отдельно исследовать топологические сортировки каждого из графов семейства, можно взять объединение этих графов и исследовать его топологическую сортировку.
Теорема
13.
Пусть
![]() - ациклические графы,
- ациклические графы,
![]() .
.
Если - ациклический, то любая топологическая сортировка графа порождает топологическую сортировку для каждого из графов [Воев].
Доказательство.
Пусть известна какая-то топологическая
сортировка графа
,
при этом все вершины каждого из графов
![]() ,
рассматриваемые как вершины графа
,
распределены некоторым образом по
группам топологической сортировки.
Возможно, что при этом в каких-то группах
не окажется ни одной вершины
.
Топологическая сортировка графа
порождает разбиение множества вершин
графа
на непересекающиеся подмножества по
принадлежности вершин к одной группе.
Присвоим каждому подмножеству индекс
порождающей его группы, получая таким
образом топологическую сортировку для
.
Действительно, в одном подмножестве
вершины графа
не являются смежными, т.к. они принадлежат
одной группе топологической сортировки
как вершины графа
.
В вершины любого подмножества дуги либо
не входят, либо входят из вершин,
принадлежащих подмножествам с меньшими
номерами, что также является следствием
того, что вершины одного подмножества
принадлежат одной группе.
,
рассматриваемые как вершины графа
,
распределены некоторым образом по
группам топологической сортировки.
Возможно, что при этом в каких-то группах
не окажется ни одной вершины
.
Топологическая сортировка графа
порождает разбиение множества вершин
графа
на непересекающиеся подмножества по
принадлежности вершин к одной группе.
Присвоим каждому подмножеству индекс
порождающей его группы, получая таким
образом топологическую сортировку для
.
Действительно, в одном подмножестве
вершины графа
не являются смежными, т.к. они принадлежат
одной группе топологической сортировки
как вершины графа
.
В вершины любого подмножества дуги либо
не входят, либо входят из вершин,
принадлежащих подмножествам с меньшими
номерами, что также является следствием
того, что вершины одного подмножества
принадлежат одной группе.
Пример *1. Вычислить значение
![]()
где
![]() ,
,
![]() ,
а
,
а
![]() ,
,![]() -
вводимые параметры.
-
вводимые параметры.
Решение
задачи может пойти по двум взаимоисключающим
путям в зависимости от соотношения
между значениями
и
,
которые являются результатами
промежуточных вычислений. Так если
![]() ,
то граф
,
то граф
![]() соответствующего алгоритма будет иметь
вид, представленный на рис.10.1(а), в
противном случае граф
соответствующего алгоритма будет иметь
вид, представленный на рис.10.1(а), в
противном случае граф
![]() алгоритма имеет вид, представленный на
рис.10.1(б).
алгоритма имеет вид, представленный на
рис.10.1(б).
Построим граф (рис.10.1(в))
![]() .
.
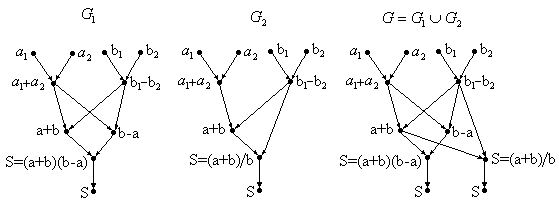
а б в
Рис.10.1.
Топологическая сортировка графа в соответствии с теоремой 13 порождает топологические сортировки и (рис.10.2).
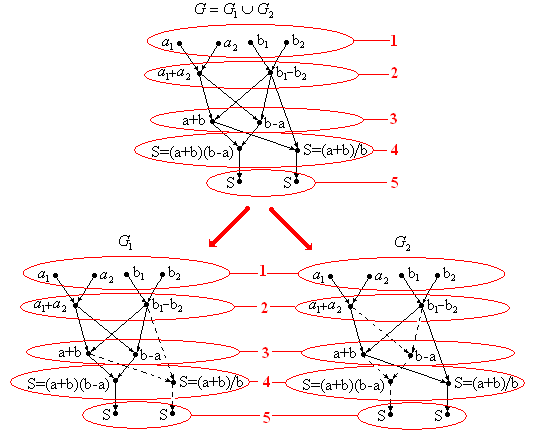
Рис.10.2.
Такой возможностью получения топологических сортировок подграфов по топологической сортировке объединения целесообразно пользоваться, когда есть какой-то выигрыш в вычислительной работе. Это прпоисходит, например, тогда, когда в «похожих» алгоритмах есть много совпадающих операций, а в соответствующих графах тогда окажется много совпадающих вершин (как в предыдущем примере). Тогда если строить топологические сортировки каждого из «похожих» алгоритмов в отдельности, на это уйдет, очевидно, больше времени, чем при построении топологической сортировки объединения.
Пример *2. Вычислить значение выражения: