2. Гомоморфная свертка. Понятие гомоморфного образа, прообраза. Связь топологических сортировок графа и его гомоморфной свертки

Операция элементарного гомоморфизма ассоциативна. Последовательность элементарных гомоморфизмов называется гомоморфной сверткой. Гомоморфной сверткой также часто называется граф, полученный в результате выполнения указанных операций. Операции, заключающиеся в последовательном выполнении простого (кратного) элементарного гомоморфизма называют простым (кратным) гомоморфизмом или простой (кратной) гомоморфной сверткой. На рис.11.3 представлены результаты последовательности 2 элементарных гомоморфизмов: 1) слияния вершин 2 и 3 исходного графа, в результате чего появилась новая вершина 9; 2) слияние 9 и 5, результатом чего стала вершина 10.

Говорят, что граф гомоморфен (просто гомоморфен) графу , если он изоморфен некоторому графу, который получается из графа с помощью гомоморфной свертки (простой гомоморфной свертки). Очевидно, что отношение гомоморфизма графов не симметрично. Граф называется гомоморфным образом (прообразом) графа . По отношению друг к другу аналогично называются их вершины и дуги.

Поскольку к гомоморфной свертке графа часто прибегают с целью уменьшения его размера и сокращения вычислительной работы при его анализе в процессе выявления параллельных форм, выясним, как связаны между собой в общем случае топологические сортировки графа и его гомоморфной свертки.

Пусть — ациклический граф, являющийся простой гомоморфной сверткой ациклического графа . Пусть известна какая-то топологическая сортировка . Разобьем вершины графа на непересекающиеся группы, относя к одной группе те из них, образы которых в графе попадают в одну группу его топологической сортировки. Присвоим группам вершин в графе индексы порождающих их групп графа . Полученное разбиение вершин графа определяет в графе обобщенную топологическую сортировку. Действительно, вершины одной группы графа являются гомоморфными прообразами вершин одной группы графа . Так как при простой гомоморфной свертке некоторые дуги могут не иметь образы, то вершины одной группы графа могут быть связаны между собой ребрами. Поэтому сортировка в графе может быть в общем случае только обощенной. Если рассмотреть любое ребро в графе , связывающее вершины из разных групп, то оно обязательно имеет образ в графе , который также связывает в вершины из разных групп. Если ребро имеет образ, и этот образ не является петлей, то при гомоморфной свертке начальная вершина всегда переходит в начальную, а конечная — в конечную. Поэтому в рассматриваемом ребре графа его начальная вершина принадлежит группе с меньшим номером, чем конечная. Таким образом, если простая гомоморфная свертка ациклического графа есть ациклический граф, то любая топологическая или обобщенная топологическая сортировка графа порождает в общем случае обобщенную топологическую сортировку графа .

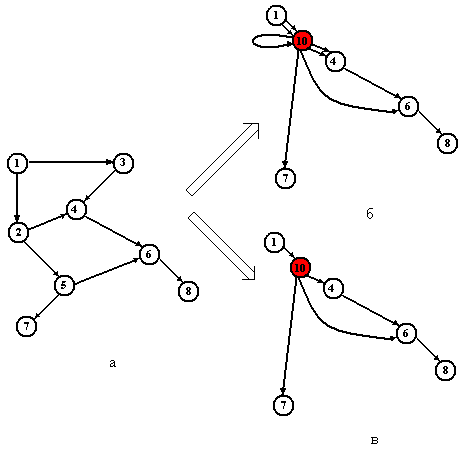
Рис.11.3. Исходный граф (а); кратная гомоморфная свертка (б); простая гомоморфная свертка

Для рассмотренного выше примера восстановление топологической сортировки исходного графа по сортировке его простой гомоморфной свертки представлено на рис.11.4.

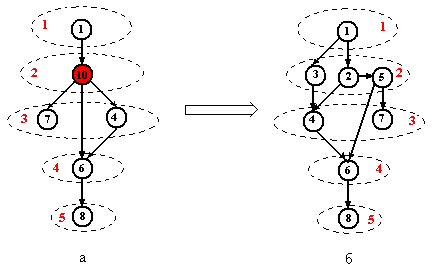
Рис.11.4. Топологическая сортировка простой гомоморфной свертки (а); восстановленная обобщенная топологическая сортировка исходного графа (б)