Расчет по раскрытию трещин, наклонных к продольной оси элемента

4.11(4.17). Ширина раскрытия трещин, наклонных к продольной оси элемента, при армировании хомутами, нормальными к продольной оси, должна определяться по формуле

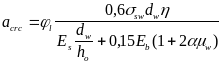(266)

где _l  коэффициент, принимаемый равным при учете:

кратковременных нагрузок и непродолжительного

действия постоянных и длительных нагрузок................. 1,00

продолжительного действия постоянных и длительных

нагрузок для конструкций из бетонов:

тяжелого:

естественной влажности............................................... 1,50

в водонасыщенном состоянии...................................... 1,20

при попеременном водонасыщении и высушивании... 1,75

мелкозернистого и легкого  то же, что в формуле (249);

  то же, что в формуле (249);

d_w - диаметр хомутов;

_sw — напряжение в хомутах, определяемое по формуле

; (267)

значение напряжения _sw не должно превышать R_s,ser;

Q_b1  правая часть условия (72) с коэффициентом _b4, умноженным на 0,8,при этом, R_bt заменяется на значение _Rbt,ser, принимаемое не более значения, соответствующего бетону класса В30;

Q — поперечная сила в конце наклонного сечения с проекцией длиной с.

Значение с принимается не более 2h_о. Если при расчете элемента на действие равномерно распределенной нагрузки выполняется условие

(268)

(где q₁  см. п. 3.32), значение с можно принимать равным только 2h_о.

Для элементов из легкого бетона класса В7,5 и ниже значение a_crc, вычисленное по формуле (266), должно быть увеличено на 30 %.

При определении ширины непродолжительного раскрытия наклонных трещин от действия всех нагрузок должны учитываться указания п. 4.10. При этом в формуле (265) коэффициент _l назначается согласно настоящему пункту, а отношение _sl/_s заменяется на отношение напряжений _swl/_sw, определяемых по формуле (267) соответственно от суммы постоянных и длительных нагрузок и от всех нагрузок.

Допускается уменьшать величину а_сrc в 1,5 раза по сравнению с определенной по формуле (266), если элемент армирован продольными стержнями того же диаметра, что и хомуты, и с расстояниями по высоте сечения, равными шагу хомутов s.

Примеры расчета

Пример 53. Дано: железобетонная плита перекрытия с размерами поперечного сечения (для половины сечения плиты) по черт. 86: b = 85 мм, h = 400 мм, b_f = 725 мм, h_f= 50 мм; бетон тяжелый класса В25; рабочая арматура класса A-III (R_s = 365 МПа; Е_s = 210⁵ МПа), расположенная в два ряда (a₁ = 58 мм; a₂ = 33 мм); площадь ее сечения А_s = 760 мм² (222) ; полный момент в середине пролета М_tot = 69 кНм; все нагрузки постоянные и длительные; из расчета по прочности известно, что М_и = 92,3 кНм и х = 30 мм.

Требуется произвести расчет по раскрытию трещин, нормальных к продольной оси элемента.

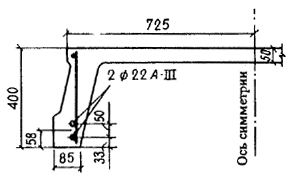
Черт. 86. К примеру расчета 53

Расчет. h_o = h  а = 400  58 = 342 мм. Так как то, согласно п. 4.1, принимаем, что элемент работает с трещинами в растянутой зоне.

Для определения продолжительного раскрытия трещин вычислим напряжение в арматуре _s. Согласно формуле (263), величина _s на уровне центра тяжести арматуры равна:

Поскольку арматура расположена в два ряда, вычислим по формуле (262) коэффициент _n:

Напряжение в нижнем стержне арматуры равно:

_s = 2731,08 = 294МПа.

Ширину раскрытия трещин находим по формуле (249). Так как , значение принимаем равным 0,02. Согласно п. 4.7,  = 1,0;  = 1,0; d = 22 мм.

что меньше предельно допустимой ширины раскрытия трещин a_crc2 = 0,3 мм.

Пример 54. Дано: железобетонная плита фундамента с размерами поперечного сечения h = 300 мм, b = 1150 мм; a = 42 мм; бетон тяжелый класса В15 (_Rbt,ser = 1,15 МПа; E_b = 2,0510⁴ МПа); рабочая арматура класса A-III (R_s = 365 МПа; Е_s = 210⁵ МПа); площадь ее сечения А_s = 923 мм² (6 14); момент в расчетном сечении от постоянных и длительных нагрузок M_l = 63 кНм, от кратковременных нагрузок M_sh = 4 кНм; предельный момент по прочности М_u = 80,5 кНм; фундамент расположен выше уровня грунтовых вод.

Требуется произвести расчет по раскрытию нормальных трещин.

Расчет. h_o = h ‑ а = 300 ‑ 42 = 258 мм. Определим необходимость вычисления ширины раскрытия трещин согласно п. 4.5. Для этого найдем момент трещинообразования M_crc.

Так как момент M_crc находим как для бетонного сечения, используя формулу (246):

M_crc = R_bt,serW_pl = 0,292bh²R_bt,ser = 0,2921150300²1,15 = 34,7510⁶ Нмм = 34,8 кНм.

Так как M_r = М_tot = M_l + М_sh = 63 + 4 = 67 кНм > M_crc = 34,8 кНм, проверка ширины раскрытия трещин необходима.

Поскольку фундамент расположен выше уровня грунтовых вод, допустимая ширина продолжительного раскрытия трещин, согласно табл. 1, поз. 4, a_crc2 = 0,3 мм, поэтому при согласно п. 4.6, расчет производим только на продолжительное раскрытие трещин от действия момента M_l.

Ширину раскрытия трещин определим по формуле (249).

Напряжение в арматуре _s вычислим по упрощенной формуле (263):

Коэффициенты, вводимые в формулу (249), принимаем равными:  = 1,0;  = 1,0; d = 14 мм, тогда

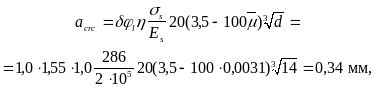
что больше допустимого значения a_crc2 = 0,3 мм, в связи с чем целесообразно произвести корректировку значения a_crc в меньшую сторону согласно п. 4.8б. Поскольку такая корректировка допускается. Так как a₂ = а = 42 мм < 0,2h = 0,2  300 = 60 мм, корректировка значения a_crc, согласно п. 4.8а, не производится.

По формуле (256) определим значение М_о, предварительно вычислив:

M_o = M_crс + bh²R_bt,ser = 34,810⁶ + 0,4541150300²1,15 = 88,810⁶ Нмм = 88,8 кНм.

Поскольку М_о = 88,8 кНм > M_r = 67 кНм, вычислим коэффициент _b по формуле (253) :

принимаем _l1 = 1;

_b = _f1_l1 = 0,79 < 1.

С учетом коэффициента _b, ширина раскрытия трещин равна a_crc = 0,340,79 = 0,269 мм < 0,3 мм, т. е. меньше предельно допустимого значения.

Пример 55. Дано: железобетонная колонна промышленного здания с размерами поперечного сечения h = 500 мм, b = 400 мм; a = a = 50 мм; бетон тяжелый класса В15 (R_b,ser = 11 МПа; R_bt,ser = 1,15 МПа; E_b = 2,0510⁴ МПа); рабочая арматура класса A-III (Е_s = 210⁵ МПа); площадь ее сечения A_s = A_s = 1232 мм² (2 28); продольная сжимающая сила N = N_l = 500 кН; момент от полной нагрузки M_tot = 240 кНм, в том числе момент от постоянных и длительных нагрузок M_l = 150 кНм.

Требуется рассчитать колонну по раскрытию трещин.

Расчет. h_o = h ‑ a = 500 ‑ 50 = 450 мм. Определим необходимость расчета по раскрытию трещин. Для этого проверим условие (233). Так как то, согласно п. 4.2, момент сопротивления W_pl находим как для бетонного сечения. Используя формулу (246), находим

M_crc = 0,292bh²R_bt,ser = 0,292400500²1,15 = 33,610⁶ Нмм.

Ядровое расстояние r определим по формуле (241). Для этого вычислим _b как для упругого тела (влиянием арматуры пренебрежем):

принимаем  = 0,7;

.

По формуле (238) определим момент M_r:

т. е. условие (233) не выполняется. Следовательно, проверка раскрытия трещин обязательна.

Поскольку согласно п. 4,6 проверим непродолжительное раскрытие трещин. Для этого в соответствии с п. 4.10 предварительно вычислим ширину продолжительного раскрытия трещин от действия усилий M_l и N_l по формуле (249). При этом воспользуемся упрощенной формулой (264) для _s.

По вычисленным значениям _f = 0,074,  = 0,067 и находим по табл. 30 значение коэффициента _crc = 0,33.

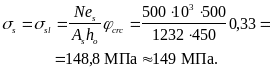
Согласно п. 4.7,  = 1,0;  = 1,00;

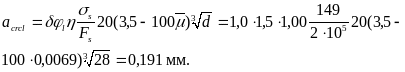
Напряжение в арматуре _s от действия всех нагрузок так же определим по формуле (264).

При _f = 0,074, = 0,067 и коэффициент _crc согласно табл. 30 равен 0,522.

Тогда, согласно формуле (265),

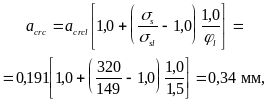
что меньше предельно допустимого значения a_crcl = 0,4 мм (см. табл. 1, поз. 4).

Пример 56. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м, нагруженная равномерно распределенными нагрузками: временной длительно действующей эквивалентной нагрузкой v = 30 кН/м и постоянной нагрузкой g = 12,5 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, h_о = 370 мм; бетон тяжелый класса В 15 (R_bt,ser = 1,15 МПа; E_b = 2,0510⁴ МПа); хомуты двухветвевые из арматуры класса А-I (Е_s = 2,110⁵ МПа) с шагом s = 150 мм, диаметром 8 мм (4_sw = 101 мм²).

Требуется произвести расчет по раскрытию наклонных трещин.

Расчет. Определим сначала необходимость расчета по раскрытию наклонных трещин, проверив условие (248).

Наибольшая поперечная сила в опорном сечении равна:

Согласно табл. 21, _b3 = 0,6.

_b3R_bt,serbh_o = 0,615200370 = 51060 H < Q_max = 117 кН,

т. е. наклонные трещины образуются и расчет по их раскрытию необходим.

Расчет производим согласно п. 4.11. Определим значения Q и Q_b1.

q₁ = g + v/2 = 12,5 + 30/2 = 27,5 кН/м;

_b4 = 1,5 (см. табл. 21).

Поскольку 0,2_b4R_bt,serb = 0,21,51,15200 = 56,9 Н/мм > q₁ = 27,5 Н/мм, значение с при определении Q_b1 и Q принимаем равным с = 2h _о = = 2370 = 740 мм.

Отсюда

Q = Q_max  q_1s = 117  27,5 0,740 = 96,65 кН .

Определим напряжение в хомутах по формуле (267):

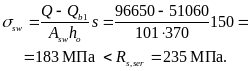
Согласно пп. 4.7 и 4.11, _l = 1,5;  = 1,3; d_w = 8 мм.

Определим ширину раскрытия наклонных трещин по формуле (266):

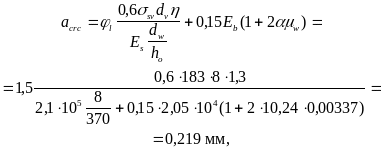
что меньше предельно допустимого значения а_сrc = 0,3 мм (см. табл. 1).