Черт. 50. К примерам расчета 38 и 40

I  граница сжатой зоны в первом приближении; II  окончательная

граница сжатой зоны

Расчет. Прочность проверим согласно п. 3.74. Оси симметрии, параллельные размерам h и b, обозначим соответственно x и y. Определим предельные моменты и . Для этого вычислим распределенное армирование A_sx и A_sy. Из черт. 50 A_{s1, x} = 0, n_x = 0, A_s0 = 804,3 мм² ( 32), A_{s1, y} = 314,2 мм² ( 20),

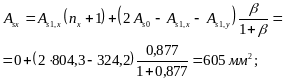
мм² (4  32 + 2  20);

мм².

При определении, согласно п. 3.63, момента , действующего в плоскости оси х, принимаем: A_sl = A_sy = 1318 мм²; A_st = A_sx = 605 мм²; h = 600 мм; b = 400 мм.

Н;

Так как 0,534 < _R = 0,55, значение определим по формуле (117), вычислив = 0,74:

При определении момента , действующего в плоскости оси y, принимаем: A_sl = A_sx = 605 мм²; A_st = A_sy = 1318 мм²; h = 400 мм; b = 600 мм;

Так как 0,583 > _R = 0,55, значение определим по формуле (118), вычислив:

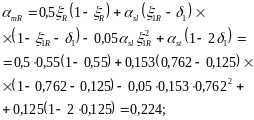
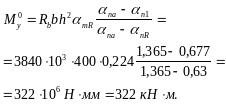
Поскольку прочность сечения проверим по графикам черт. 42, а, б, соответствующим _s = 0,2 и _s = 0,4. На обоих графиках точка с координатами = 240/464,7 = 0,516 и = 182,5/322 = 0,566 лежит внутри области, ограниченной кривой, отвечающей параметру _n1 = 0,677, и осями координат.

Следовательно, прочность сечения обеспечена.

Пример 39. Дано: сечение колонны, характеристики материалов и значение продольной силы от всех нагрузок  из примера 33; в сечении одновременно действуют изгибающие моменты в плоскости, параллельной размеру h, – M_x = 3330 кН·м и в плоскости, параллельной размеру b, – M_y = 396 кН·м; моменты М_х и М_y даны с учетом прогиба колонны.

Требуется проверить прочность сечения.

Расчет. Прочность проверим согласно п. 3.75. Определим предельный момент , действующий в плоскости оси симметрии х, проходящей в ребре. Согласно примеру 33, правая часть условия (131) равна 5847 кН·м, тогда

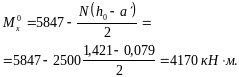
Предельный момент , действующий в плоскости оси симметрии y, нормальной к ребру, определим как для прямоугольного сечения, составленного их двух полок, согласно п. 3.63. Тогда, согласно черт. 49, имеем: h = 600 мм; b = 2 · 215 = 430 мм.

Определим распределенное армирование A_sl и A_st:

мм² ( 32); _l = 3;

мм² (14  32);

A_sl = A_{s1, l} (n_l + 1) = 804,3 (3 + 1) = 3220 мм²;

A_st = A_{s, tot}/2 – A_sl = 11 260/2 – 3220 = 2410 мм².

Из табл. 18 находим  = 0,698 и _R = 0,523.

R_bbh = 19 · 430 · 600 = 4902 · 10³ H;

₁ = a₁/h = 0,083;

Значение определим по формуле (117), вычислив

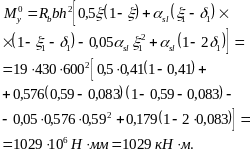
Проверим прочность сечения, принимая b = 200 мм, h = 1500 мм.

Поскольку прочность сечения проверим по графикам черт. 44, б, в, соответствующим _s = 0,6 и _s = 1,0.

На обоих графиках точка с координатами = 3330/4170 = 0,8 и = 396/1029 = 0,385 лежит внутри области, ограниченной кривой, отвечающей параметру _n1 = N/(R_bbh) = 2500 · 10³/(19 · 200 · 1500) = 0,44, и осями координат.

Следовательно, прочность сечения обеспечена.

Пример 40. Дано: прямоугольное сечение колонны размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (R_b = МПа при _b2 = 1,1); продольная арматура класса A-III (R_s = 365 МПа) по черт. 50; в сечении одновременно действуют продольная сила N = 2600 кН и изгибающие моменты в плоскости, параллельной размеру h, – М_х = 250 кН·м и в плоскости, параллельной размеру b, M_y = 200 кН·м; изгибающие моменты М_х и M_y даны с учетом прогиба колонны.

Требуется проверить прочность сечения, пользуясь формулами п. 3.76 для общего случая расчета.

Расчет. Все стержни обозначим номерами, как показано на черт. 50. Через центр тяжести наиболее растянутого стержня 5 проводим ось х параллельно размеру h = 600 мм и ось y параллельно размеру b.

Угол  между осью y и прямой, ограничивающей сжатую зону, принимаем, как при расчете упругого тела на косое внецентренное сжатие, т. е.:

Задаваясь значением х₁  размером сжатой зоны по наиболее сжатой стороне сечения h, можно определить для каждого стержня отношение _i = x/h_0i по формуле где a_xi и a_yi расстояния от i-го стержня до наиболее сжатой стороны сечения в направлении осей соответственно х и у.

По значениям _i определим напряжение _si, принимая _sc,u = 400 МПа,  = 0,722 (см. табл. 18):

При этом, если _si > R_s = 365 МПа, что равносильно условию _i < _R = 0,55 (см. табл. 18), принимаем _si < R_s = 365 МПа.

Если _si < –R_sc = –365 МПа, принимаем _si = –365 МПа.

Последнее условие после подстановки в него выражения для _si приобретет вид

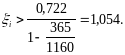
Затем определим сумму усилий во всех стержнях A_si_si.

Задаваясь в первом приближении значением x₁ = h = 600 мм, произведем указанные вычисления, результаты которых приводим в следующей таблице:

Номер	Asi,	ayi,	axi,	ayitg + axi,	х1 = 600 мм			х1 = 660 мм
стержня	мм2	мм	мм	мм (tg = 1,8)	i	si, МПа	Asisi, H	i	si, МПа	Asisi, H
1	804,3	350	50	680	0,882	–210	–168 900	0,971	–297	–238 877
2	804,3	50	50	140	4,29	–365	–293 570	4,714	–365	–293 570
3	314,2	350	300	930	0,645	138	43 360	0,71	20	6284
4	314,2	50	300	390	1,54	–365	–114 683	1,692	–365	–114 683
5	804,3	350	550	1180	0,508	365	293 570	0,56	339	272 658
6	804,3	50	550	640	0,937	266	213 944 Asisi = –26 280 H	1,031	–348	–279 896 Asisi = –648 080 H

Так как мм < b = 400 мм, форма сжатой зоны треугольная и площадь ее равна:

мм².

Проверим условие (154):

т. е. площадь сжатой зоны занижена.

Увеличим значение х₁ до 660 мм и аналогично определим A_si_si (см. таблицу к настоящему примеру).

При х₁ > h и х₁/tg = 660/1,8 = 367 мм < b = 400 мм форма сжатой зоны трапециевидная и площадь ее равна:

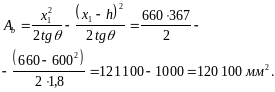
Поскольку R_bA_b – A_si_si = 16 · 120 100 + 648 080 = 2570 · 10³ H = 2570 кН  N = 2600 кН, условие (154) соблюдается.

Определим моменты внутренних сил относительно осей у и х. Для этого определим статические моменты площади сечения сжатой зоны относительно этих осей:

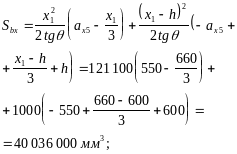
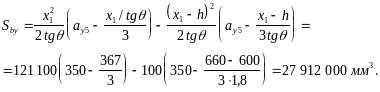
Тогда M_xu = R_bS_bx – A_si_si (а_х5 – а_xi) = 16 · 40 036 000 – [–238 877 (550 – 50) – 293 570 (550 – 50) + 6284 (550 – 300) – 114 683 (550 – 300)] = 933,9 · 10⁶ Н · мм = 934 кН · м;

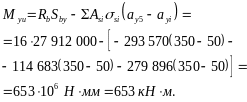
Моменты внешних сил относительно осей у и х равны:

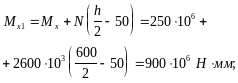
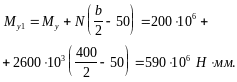
Поскольку M_xu >M_x1, а M_yu > M_y1 прочность сечения обеспечена.

РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ

Пример 41. Дано: колонна многоэтажного каркаса с сечением размерами b = 400 мм, h = 600 мм; а = а = 50 мм; бетон тяжелый класса В25 (R_bt = 0,95 МПа при _b2 = 0,9); хомуты, расположенные по граням колонны, из арматуры класса A-III, диаметром 10 мм (R_sw = 255 МПа; A_sw = 157 мм²), шагом s = 400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны M_sup = 350 кН·м, M_inf = 250 кН·м и растягивают соответственно левую и правую грани колонн; продольная сила N = 572 кН; длина колонны (расстояние между опорными сечениями) l = 2,8 м.

Требуется проверить прочность наклонных сечений колонны по поперечной силе.

Расчет. h₀ = h – a = 600 – 50 = 550 мм. Расчет производим согласно п. 3.31 с учетом рекомендаций п. 3.53.

Поперечная сила в колонне равна:

кН.

Поскольку поперечная сила постоянна по длине колонны, длину проекции наклонного сечения принимаем максимально возможной, т. е. равной

Определим коэффициент _n:

Поскольку с = с_max, Q_b = Q_b,min = _b3 (1 + _n)R_btbh₀ = 0,6 (1 + 0,27)0,95 · 400 · 550 = 159,2 · 10³ H < Q = 214 кН, т. е. хомуты требуются по расчету.

Значение q_sw определим по формуле (55):

Н/мм.

Проверим условие (57):

Поскольку условие (57) не выполняется, определим значение M_b по формуле

откуда

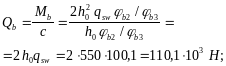
с₀ принимаем равным с₀ = 2h₀ = 2 · 550 = 1100 мм, тогда Q_sw = q_swc₀ = 100,1 · 1100 = 110,1 · 10³ Н.

Проверим условие (50):

т. е. прочность сечений по поперечной силе обеспечена.