Прямоугольные сечения с несимметричной арматурой

Пример 31. Дано: сечение элемента размерами b = 400 мм, h = 500 мм; a = a' = 40 мм; бетон тя­желый класса B25 (R_b = 13 МПа при _b2 = 0,9; E_b = 2,7 · 10⁴); арматура класса A-III (R_s = R_sc = 365 МПа); продольная сила N = 800 кН; ее эксцентриситет относительно центра тяжести бетон­ного сечения е₀ = 500 мм; расчетная длина l₀ = 4,8 м.

Требуется определить площади сечения армату­ры S и S’.

Расчет. h₀ = 500 – 40 = 460 мм. Так как 4 < l₀/h = 4,8/0,5 = 9,6 < 10, расчет производим с учетом прогиба элемента согласно п. 3.54. При этом, предположив, что   0,025, значение N_cr определим по упрощенной формуле

Коэффициент  вычислим по формуле (91):

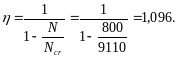
Значение e с учетом прогиба элемента равно:

мм.

Требуемую площадь сечения арматуры S’ и S оп­ределим по формулам (121) и (122):

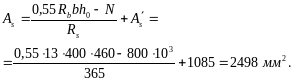
Поскольку 0,018 < 0,025, значения А_s и не уточняем.

Принимаем = 1232 мм² (2  28), А_s = 2627 мм² (2  32 + 1  36).

Элементы с косвенным армированием

Пример 32. Дано: колонна связевого каркаса с размерами сечения и расположением арматуры по черт. 48; бетон тяжелый класса В40 (R_b = 20 МПа при _b2 = 0,9; R_b,ser = 29 МПа; E_b = 3,25 · 10⁴ МПа); продольная арматура класса A-VI; сетки косвенного армирования из стержней класса A-III, диаметром 10 мм (R_s,xy = 365 МПа), рас­положенные с шагом s = 130 мм по всей длине ко­лонны; продольная сила при _f > 1,0: от всех наг­рузок N = 6600 кН, от постоянных и длительных нагрузок N_l = 4620 кН; то же, при _f = 1,0: N = 5500 кН и N_l = 3850 кН; начальный эксцентри­ситет продольной силы e₀ = e_a = 13,3 мм; расчет­ная длина колонны l₀ = 3,6 м.

Требуется проверить прочность колонны.

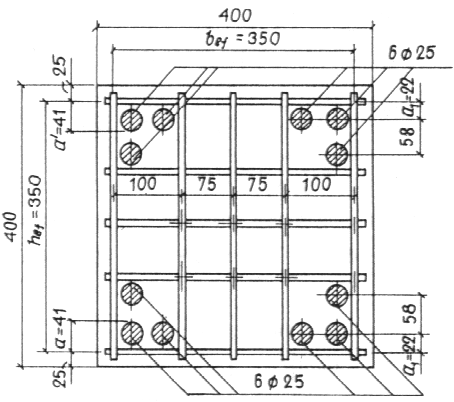
Черт. 48. К примеру расчета 32

Расчет. Проверим прочность сечения, заклю­ченного внутри контура сеток, с учетом косвенного армирования согласно п. 3.57. Расчетные размеры сечения h_ef = b_ef = 350 мм. Поскольку l₀/h_ef = 3600/350 = 10,3 < 16, косвенное армирование можно учитывать при расчете, при этом следует учи­тывать прогиб колонны согласно пп. 3.54 и 3.58, так как l₀/h_ef > 4.

Принимая l₀/c_ef = l₀/h_ef = 10,3 и h = h_ef = 350 мм, получим

Следовательно, принимаем _e = _e,min = 0,297. Поскольку промежуточные стержни продольной арматуры располагаются в крайних четвертях рас­стояния между крайними стержнями, равного h –2a₁ = 350 – 2 · 22 = 306 мм [58 мм < = 76,5 мм (см. черт. 48)], согласно примечанию к п. 3.63 принимаем арматуру S и S’ как сосредоточенную по линиям их центров тяжести. Тогда, учиты­вая, что все стержни одинакового диаметра, имеем:

мм;

мм.

Коэффициент _l определим по формуле (94), принимая  = 1,0 (см. табл. 16) и

Значение критической силы N_cr определим по формуле (93), принимая

мм² (6  25),

и умножая полученное значение на коэффициент _l = 0,25 + 0,05 = 0,25 + 0,05 · 10,3 = 0,764:

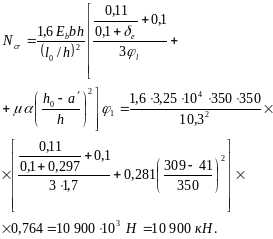
Коэффициент  равен:

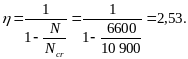
Отсюда, согласно формуле (111),

мм.

Определим приведенную призменную прочность R_b,red согласно п. 3.57.

Принимая А_sx = А_sy = 78,5 мм² ( 10), n_x = n_y = 5, l_x = l_y = 350 мм и A_ef = h_efb_ef = 350 · 350 = 122 500 мм² (см. черт. 48), вычислим коэффициент

тогда

МПа.

Поскольку здесь применена высокопрочная арма­тура класса A-VI, приведенное расчетное сопротив­ление арматуры сжатию определим согласно п. 3.59:

мм²;

Принимаем  = 1,6.

Из табл. 25 ₁ = 2,04, ₂ = 0,77, R_sc = 500 МПа, R_s = 815 МПа,

тогда

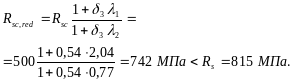
Прочность сечения проверим из условия (108), определяя высоту сжатой зоны х = h₀ по формуле (110а).

Для этого по формуле (104) определим значение . Поскольку 10_xy = 10 · 0,0173 = 0,173 > 0,15, принимаем ₂ = 0,15, тогда  = 0,85 – 0,008 R_b + ₂ = 0,85 – 0,008 · 20 + 0,15 = 0,84  0,9.

Определим, согласно пп. 3.61 и 3.65, необходи­мые коэффициенты _n, _s, и _c, приняв R_b = R_b,red = 34,3 МПа; _sc,u = 380 + 1000 ₃ = 380 + 1000 · 0,54 = 920 МПа < 1200 МПа и R_sc = R_sc,red = 742 МПа:

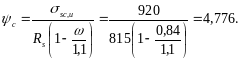
Отсюда

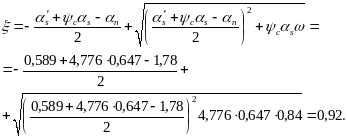
Значение _R с заменой R_s на 0,8R_s равно:

т . е. использование формулы (110a) оправдано;

мм;

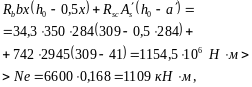
т. е. прочность сечения обеспечена.

Проверим трещиностойкость защитного слоя колонны аналогичным расчетом на действие силы N = 5500 кН (при _f = 1,0), принимая, согласно п. 3.60, R_b = R_b,ser = 29 МПа, R_s = R_s,ser = 980 МПа, R_sc = 400 МПа, _sc,u = 400 МПа,  = 0,85 – 0,006 R_b,ser = 0,85 – 0,006 · 29 = 0,679 и рассматривая полное сечение колонны, т. е. b = h = 400 мм, a = a =41 + 25 = 66 мм, h₀ = 400 – 66 = 334 мм.

Критическую силу N_cr определим по формуле (93), принимая l₀/h = 3600/400 = 9, e₀/h = 13,3/400 = 0,033, _e,min = 0,5 – 0,01 – 0,008 R_b,ser = 0,5 – 0,01 · 9 – 0,008 · 29 = 0,178 > e₀/h, т. е. _e = _e,min = 0,178.

При определении коэффициента _l учитываем продольные силы N и N_l при _f = 1,0, т. е.

тогда _l = 1 + 0,7 = 1,7;

Коэффициент равен:

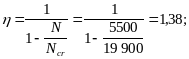
мм.

Произведем расчет аналогично расчету на прочность:

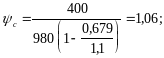
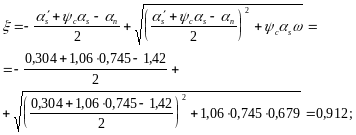
мм;

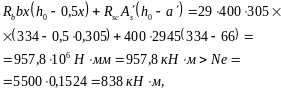
т. е. трещиностойкость защитного слоя обеспечена.

ДВУТАВРОВЫЕ СЕЧЕНИЯ

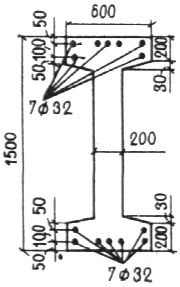
Пример 33. Дано: размеры сечения и расположение арматуры  по черт. 49; бетон тяжелый класса В30 (E_b = 2,9 · 10⁴ МПа; R_b = 19 МПа при _b2 = 1,1); арматура класса А-III (R_s = R_sc = 365 МПа); площадь ее поперечного сечения A_s = A_s = 5630 мм² (7  32); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок N_l = 2000 кН, M_l = 2460 кН·м; от всех нагрузок N = 2500 кН, М = 3700 кН·м; расчетная длина элемента: в плоскости изгиба l₀ = 16,2 м, из плоскости изгиба l₀ = 10,8 м; фактическая длина элемента l = 10,8 м.

Требуется проверить прочность сечения.