3.3.5. Теорема про рух центра мас системи

Нехай матеріальна система складається з точок. До точки з масою прикладені – рівнодійна зовнішніх сил і – рівнодійна внутрішніх сил, які діють на цю точку.

На підставі рівняння (3.5) складаємо диференціальні рівняння руху точок системи:

. (3.150)

Додамо їх почленно

. (3.151)

Перший член у правій частині рівності (3.151) є головним вектором зовнішніх сил, а другий — головним вектором внутрішніх сил, який дорівнює нулеві. Тому

, (3.152)

але

на підставі означення радіуса-вектора центра мас.

Підставляючи цей вираз у (3.152), дістанемо

. (3.153)

Порівнюючи (3.153) з (3.5), зазначаємо, що

центр мас матеріальної системи рухається як матеріальна точка, маса якої дорівнює масі системи, під дією сили, що дорівнює головному вектору зовнішніх сил, прикладених до точок системи.

Векторній рівності (3.153), яка складає зміст теореми про рух центра мас, відповідають три рівняння в координатній формі:

, (3.154)

де – проекції на осі координат головного вектора зовнішніх сил .

Рівняння (3.154) можна розглядати як диференціальні рівняння поступального руху твердого тіла.

Якщо головний вектор зовнішніх сил дорівнює нулеві, то згідно з (3.153) прискорення центра мас відсутнє, і центр мас рухається рівномірно та прямолінійно, тобто йдеться про збереження руху центра мас.

Таким чином, внутрішні сили змінити рух центра мас неспроможні.

Для того, щоб центр мас не змінював свого положення, потрібно, щоб у початковий момент часу його швидкість дорівнювала нулеві.

3.3.6. Теореми про зміну кількості руху системи і зміну кінетичного моменту

Як висновок з рівності (3.153) і означення кількості руху системи, яка дорівнює , дістанемо теорему про зміну кількості руху в диференціальній форму:

, (3.155)

або:

швидкість точки, яка креслить годограф вектора кількості руху матеріальної системи, дорівнює головному вектору зовнішніх сил, прикладених до точок системи.

На рис. 3.33 зображено траєкторію центра мас системи.

Рисунок 3.33

Помножимо ліву й праву частини (3.155) на і проінтегруємо їх:

.

Звідси

. (3.156)

Вираз називають елементарним імпульсом головного вектора зовнішніх сил, а вираз

повним імпульсом головного вектора зовнішніх сил.

Рівність (3.156) є векторною формою теореми про зміну кількості руху системи, або теореми імпульсів:

приріст кількості руху системи за певний проміжок часу дорівнює повному імпульсу головного вектора зовнішніх сил, які прикладені до точок системи.

Векторній рівності (3.156) відповідають три скалярних рівняння

(3.157)

які застосовують при розв’язуванні конкретних задач.

Закон збереження кількості руху системи виконується за тих самих умов, що й закон збереження руху центра мас, тобто, коли .

Дійсно,

якщо , то із (3.156) випливає

тобто

. (3.158)

Грунтуючись на теоремі імпульсів, можна дістати рівняння руху точки змінної маси, як це зробив І.В.Мещерський наприкінці ХІХ ст.

Введемо поняття моменту кількості руху матеріальної точки відповідно до означення моменту вектора (1.11):

, (3.159)

де – радіус-вектор точки відносно центра моментів О (рис. 3.34).

Рисунок 3.34

Проекції вектора на осі декартової системи координат, початок якої знаходиться в точці О, називають моментами кількості руху відносно координатних осей:

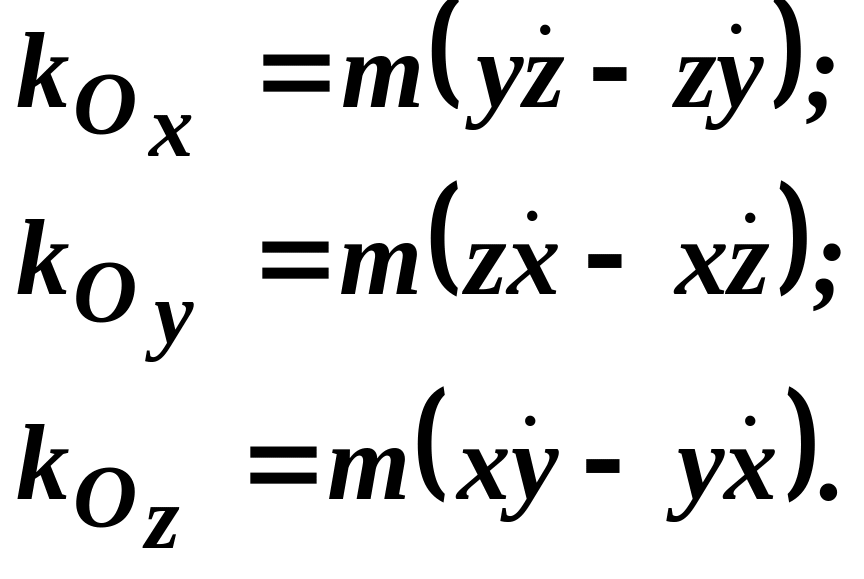(3.160)

Теорема про зміну кількості руху випливає з другого закону І.Ньютона (3.3).

Помножимо ліву і праву частини (3.3) зліва векторно на радіус-вектор :

.

Виразимо ліву частину за допомогою похідної від векторного добутку

. (3.161)

Тут , оскільки , а .

За означенням (1.11) добуток є моментом рівнодійної відносно центра О.

Отже, остаточно з (3.161) і (3.159) дістаємо

, (3.162)

тобто

похідна за часом від моменту кількості руху матеріальної точки відносно центра О дорівнює моменту рівнодійної сил, прикладених до точки, відносно того самого центра О.

Векторній рівності (3.162) відповідають три скалярних рівняння:

(3.163)

Указана теорема вперше була застосована для дослідження руху точки під дією центральної сили.

Якщо вибрати центр моментів О у фіксованій точці, через яку проходить центральна сила, то її момент відносно точки дорівнюватиме нулеві:

.

Тоді з рівняння (3.162) випливає

, (3.164)

де – векторна стала інтегрування (визначається з початкових умов).

Рівність (3.164) відповідає закону збереження моменту кількості руху точки.

З цього закону випливають два висновки.

Висновок 1. Траєкторія точки – плоска крива. Дійсно, вектор за означенням (3.159) перпендикулярний до площини, в якій розміщені вектори і , але вектор – сталий. Отже, площина весь час перпендикулярна до того самого вектора, тобто її положення в просторі не змінюється.

Висновок 2. Модуль вектора сталий. Введемо поняття секторної швидкості , що характеризує бистроту зміни площі, яку описує у просторі радіус-вектор точки М (рис. 3.35):

, (3.165)

де – площа сектора із зазначеним напрямом.

Рисунок 3.35

Обчислюючи границю, дістаємо

. (3.166)

Враховуючи (3.159) і (3.166) приходимо до висновку, що

. (3.167)

Другий висновок із (3.164):

якщо точка рухається під дією центральної сили, то її секторна швидкість стала, тобто її радіус-вектор за однакові проміжки часу окреслює однакові площинні елементи.

Рівність (3.167) визначає теорему площ, окремим випадком якої є другий закон Кеплера.

Поширимо поняття моменту кількості руху на систему точок.

Головний момент кількості руху системи матеріальних точок, або кінетичний момент, дорівнює векторній сумі моментів кількостей руху точок, що входять до системи:

. (3.168)

Для суцільного середовища

. (3.169)

Застосовуючи до однієї з точок матеріальної системи теорему (3.162), записуємо

, (3.170)

де – момент рівнодійної зовнішніх сил;

– момент рівнодійної внутрішніх сил відносно центра О.

Складемо рівності (3.170)

,

але

.

За означенням головний момент зов- нішніх сил.

Остаточно

. (3.171)

Ця рівність виражає теорему про зміну кінетичного моменту системи:

похідна за часом від кінетичного моменту системи відносно центра О дорівнює головному моменту зовнішніх сил, прикладених до точок системи, обчисленому відносно того самого центра О.

Проектуючи рівність (3.171) на осі декартової системи координат, дістаємо три рівняння

. (3.172)

Величини , а також називають відповідно кінетичними моментами і головними моментами сил відносно координатних осей.

Закон збереження кінетичного моменту виконується тоді, коли головний момент зовнішніх сил відносно центра О або відносно певної осі дорівнює нулеві:

а) якщо , то

; (3.173)

б) якщо, наприклад, , то

. (3.174)

Обчислимо кінетичні моменти тіла для окремих випадків.

Випадок 1. Якщо тіло має нерухому точку, то швидкість певної точки тіла .

На підставі (3.169) знаходимо проекції вектора на осі декартової системи координат:

. (3.175)

Аналогічно

;

.

Випадок 2. Якщо тіло обертається навколо нерухомої осі, наприклад, , то і

. (3.176)

Якщо вісь є головною віссю інерції, то і . Тоді з (3.176) знайдемо

. (3.177)

Ця рівність виражає кінетичний момент тіла з нерухомою віссю відносно цієї осі. Його часто використовують при розв’язуванні задач.

Особливо це зручно в тих випадках, коли розглядається обертальний рух твердого тіла навколо нерухомої осі. Припустимо, що це вісь . Тоді на підставі (3.177) маємо:

З (3.172) і (3.177) дістанемо

, або .

Отримане рівняння або його варіанти у вигляді

називають диференціальним рівнянням обертального руху твердого тіла навколо нерухомої осі.