3.2. Динаміка системи матеріальних точок

3.2.1. Основні поняття

У підрозд. 1.1.3 дано означення фізичної в’язі. Запровадимо поняття рівняння в’язі.

Спочатку розглянемо в’язь у вигляді поверхні певного тіла, по якій рухається точка. Умовимося про координатний спосіб визначення руху. Аналітична умова знаходження точки на поверхні полягає у тому, що її координати задовольняють рівняння цієї поверхні:

. (3.54)

Рівняння (3.54) називають рівнянням в’язі.

Якщо поверхня рухається, то до (3.54) повинен входити час :

. (3.55)

Таку в’язь називають нестаціонарною, а в’язь (3.54) – стаціонарною.

Якщо точка рухається по кривій (наприклад, кільце рухається вздовж дроту), яка описується системою двох рівнянь, то в’язь аналітично визначається системою рівнянь

(3.56)

тобто одна фізична в’язь має два рівняння. Тут і надалі кількість в’язей визначається кількістю рівнянь, якими описуються в’язі.

Наведемо ще приклад. Нехай дві матеріальні точки і з’єднані прямим абсолютно твердим стержнем довжиною . Рівняння в’язі повинно відображати незмінність відстані між точками і :

, (3.57)

де – координати точок .

Якщо довжина стержня змінна, до правої частини (3.57) повинен входити час . Отже, рівняння нестаціонарної в’язі у загальному випадку має бути функцією, яка зв’язує координати точок системи з часом і відображає особливості в’язі:

, (3.58)

де – кількість точок, що належать системі.

Кількість рівнянь типу (3.58) є кількістю в’язей.

Якщо до рівняння в’язі входять лише координати точок і час, то в’язь називають геометричною нестаціонарною.

У складнішому випадку, крім координат точок і часу, функція може залежати й від похідних за часом від координат точок:

. (3.59)

Таку в’язь називають кінематичною (диференціальною). Один приклад найпростішої кінематичної в’язі завжди наводиться у підручниках. Це – горизонтальна площина, по якій без ковзання котиться куля. Справді, точка А дотику кулі до площини має нульову швидкість, тому умова

є рівнянням кінематичної в’язі у векторній формі.

Якщо рівняння (3.59) можна проінтегрувати, то дістанемо геометричну в’язь. У цьому разі первісне рівняння називають рівнянням голономної (інтегрованої) в’язі.

Розглянемо лише геометричні в’язі.

Припустимо, що на точок системи накладено k в’язей типу (3.58). Тоді з 3 координат точок залишаються незалежними лише , оскільки k координат зв’язані між собою залежностями.

Кількістю степенів вільності системи називають кількість незалежних координат (параметрів), які однозначно визначають положення точок системи.

Наприклад, якщо точка рухається у просторі по кривій, то вона має одну степінь вільності, бо три координати точки зв’язані між собою двома рівняннями типу (3.56). Отже, кількість степенів вільності

. (3.60)

Наведемо ще приклади.

Тіло, яке обертається навколо нерухомої осі, має одну степінь вільності, оскільки положення всіх його точок визначаються одним параметром — кутом обертання навколо осі.

	Кривошипно-шатунний механізм (рис. 3.10) також має одну степінь вільності, оскільки координати будь-якої точки повністю визначаються кутом обертання кривошипа ОА навколо осі О. Припустимо, є система матеріальних точок, масою
Рисунок 3.10

прикладено сили, що надають точкам однакові прискорення , до яких. Згідно з другим законом І.Ньютона можна знайти сили, які є паралельними між собою:

. (3.61)

Центром мас (центром інерції) системи називають центр паралельних сил, які надають точкам системи поступального руху.

Радіус-вектор центра мас позначатимемо і на підставі формули (1.55) визначатимемо

, (3.62)

тут – маса системи.

Декартові координати центра мас знаходять за формулами

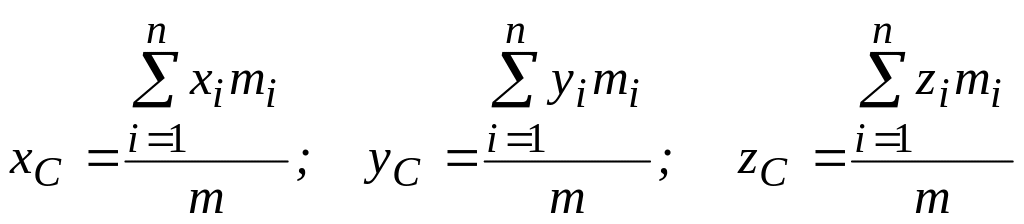. (3.63)

Якщо помножити чисельник і знаменник правих частин кожного виразу (3.63) на прискорення , то матимемо координати центра ваги системи. Це свідчить про те, що центр мас збігається з центром ваги, якщо останній існує; уявлення про центр мас ширше за уявлення про центр ваги.

Кількістю руху матеріальної системи називають векторну суму кількостей руху точок системи:

. (3.64)

Якщо система є суцільним середовищем з неперервним розподілом мас, то кількість руху визначається за допомогою інтегрування

.

Але, щоб уникнути інтегрування в кожному окремому випадку, доведемо теорему, згідно з якою

кількість руху системи дорівнює кількості руху матеріальної точки, маса якої дорівнює масі системи, а швидкість дорівнює швидкості центра мас системи.

Запишемо формулу (3.62) у вигляді

,

а потім продиференціюємо праву і ліву частини один раз за часом:

.

Сума в правій частині дорівнює кількості руху системи. Отже,

. (3.65)

Вираз (3.65) свідчить, що кількість руху не завжди може визначати міру руху системи, тобто її динамічні властивості, оскільки при кількість руху системи . Але система може, наприклад, обертатися навколо центра мас, тобто рухатися.

Кількість руху характеризує повністю динамічні властивості системи лише при її поступальному русі.

Зауважимо, що кількість руху є так званою першою мірою руху, або мірою Декарта.