Приклади

Приклад 3.4. Обчислимо роботу сили ваги в однорідному полі сили ваги. Застосуємо координатний спосіб, при якому напрямлена вниз по вертикалі (рис. 3.22).

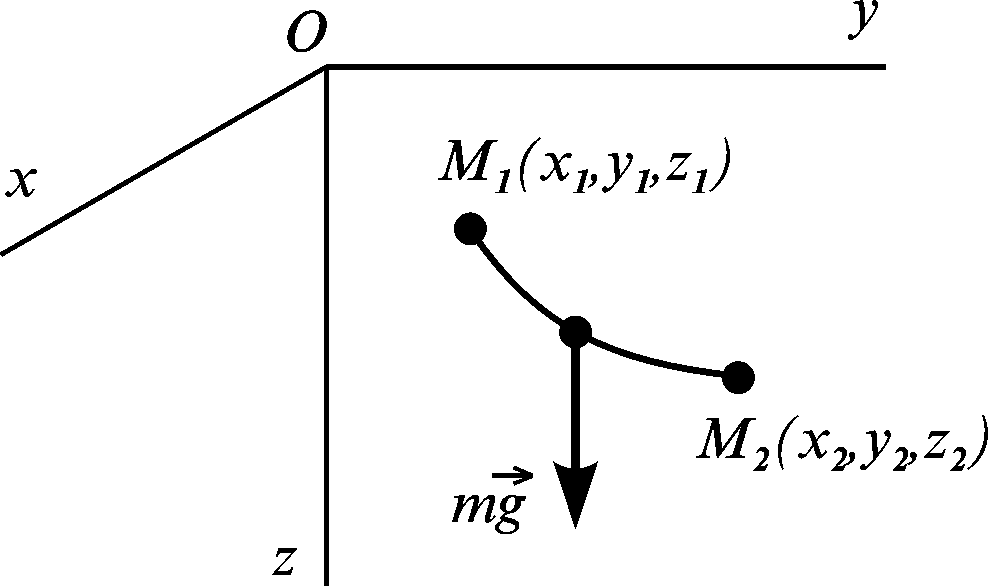
Рисунок 3.22

Матеріальна точка М переходить з точки у точку . Проекції сили ваги дорівнюють .

На підставі (3.96)

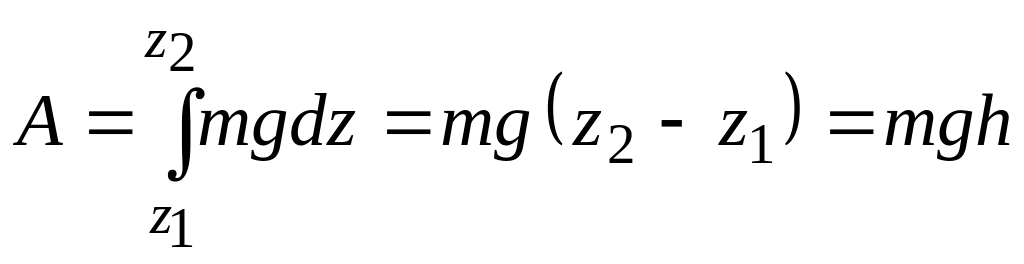, (3.99)

де – відстань по вертикалі між точками і .

Отже,

робота сили ваги не залежить від форми траєкторії точки, а залежить лише від координат z її кінцевого і початкового положень.

Знак роботи залежить від знаку різниці .

Таким чином

.

Приклад 3.5. Визначимо роботу центральної сили.

Силу називають центральною, якщо її лінія дії весь час проходить через фіксовану точку простору О.

Наприклад, сили всесвітнього тяжіння, електромагнітної взаємодії тощо. Їх величина залежить лише від відстані точки від центра притягання або відштовхування, тобто (рис. 3.23).

Введемо орт напряму радіуса-вектора точки

. (3.100)

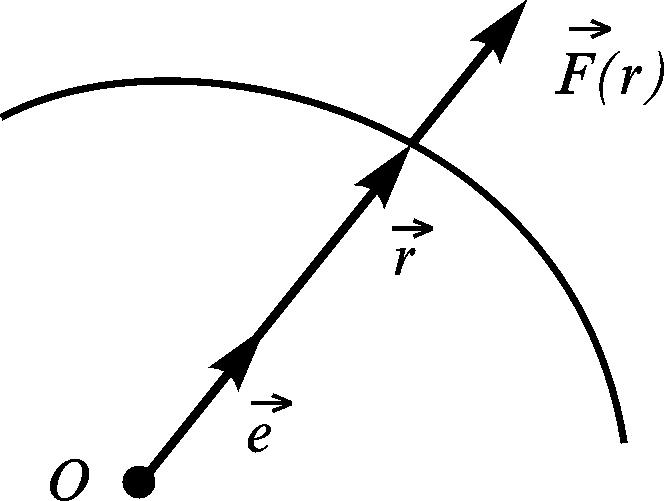
Рисунок 3.23

Тоді вектор сили

,

де — проекція на напрям , яка може бути додатною (при відштовхуванні) або від’ємною (при притягуванні точки до центра).

Елементарна робота

. (3.101)

Обчисливши

,

підставимо цей вираз у (3.101) і дістанемо

, (3.102)

де — приріст модуля радіуса-вектора точки (рис. 3.24).

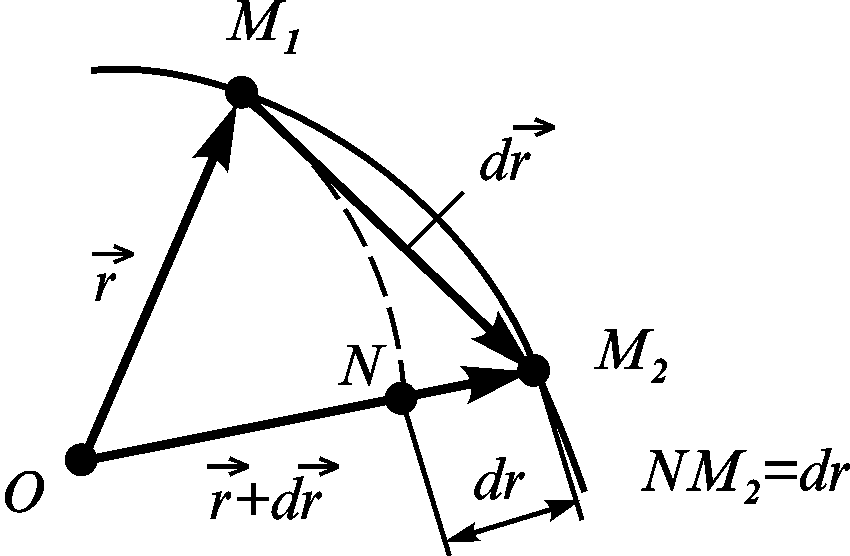
Рисунок 3.24

Повна робота А центральної сили

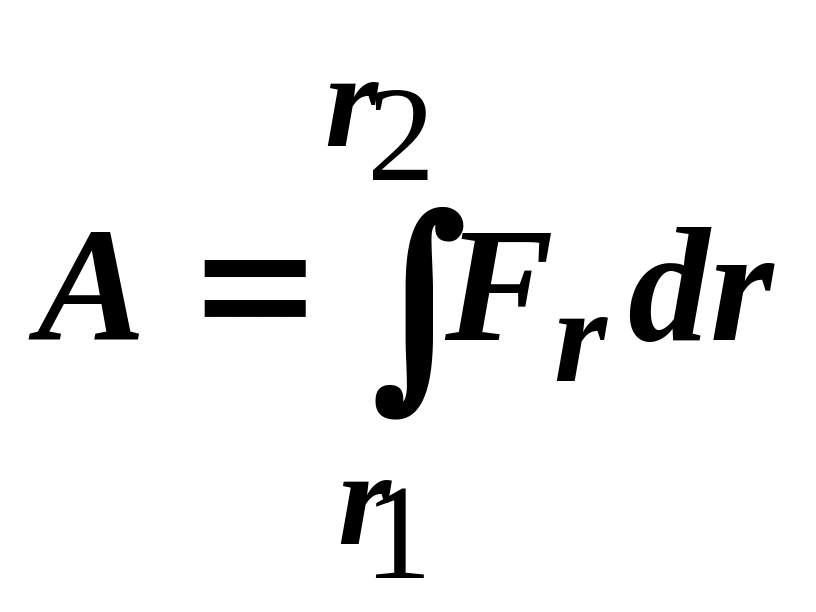. (3.103)

Як видно з (3.103),

робота центральної сили також не залежить від форми траєкторії точки, а залежить лише від її початкового і кінцевого положень.

Як приклад застосування формули (3.103) обчислимо роботу пружної сили.

Нехай пружину ВМ прикріплено кінцем В до нерухомого сферичного шарніра, точка М описує просторову криву (рис. 3.25). Довжину недеформованої пружини позначимо через . Якщо припустити, що в положенні ВМ пружину розтягнуто, то сила

,

де — коефіцієнт жорсткості пружини; .

Із (3.103) дістанемо

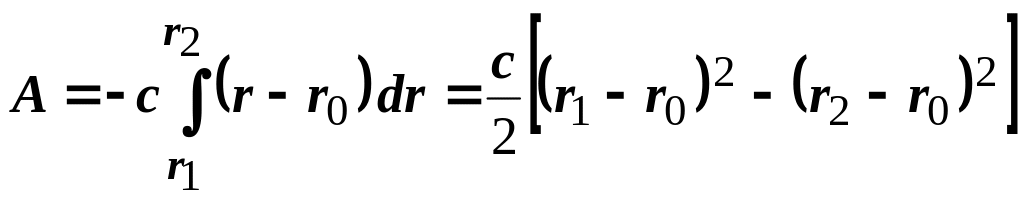. (3.104)

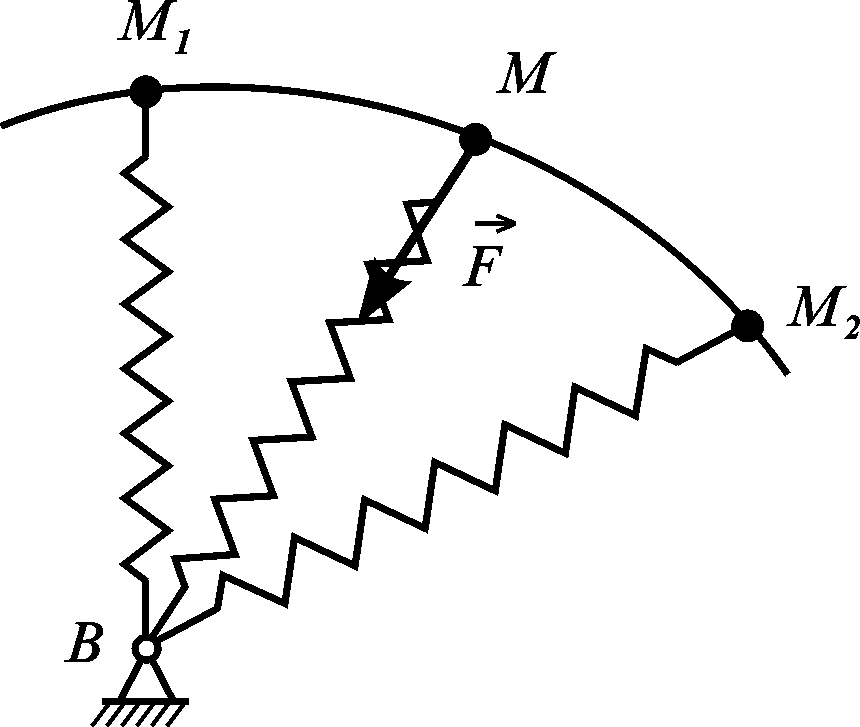
Рисунок 3.25

Приклад 3.6. Розглянемо простіший випадок, коли точка М, яку прикріплено до пружини, рухається вздовж вертикалі (рис. 3.26). Нехай у початковий момент часу пружина недеформована. Елементарна робота сили пружності у довільному положенні точки М, коли вона рухається вниз, на підставі (3.97)

.

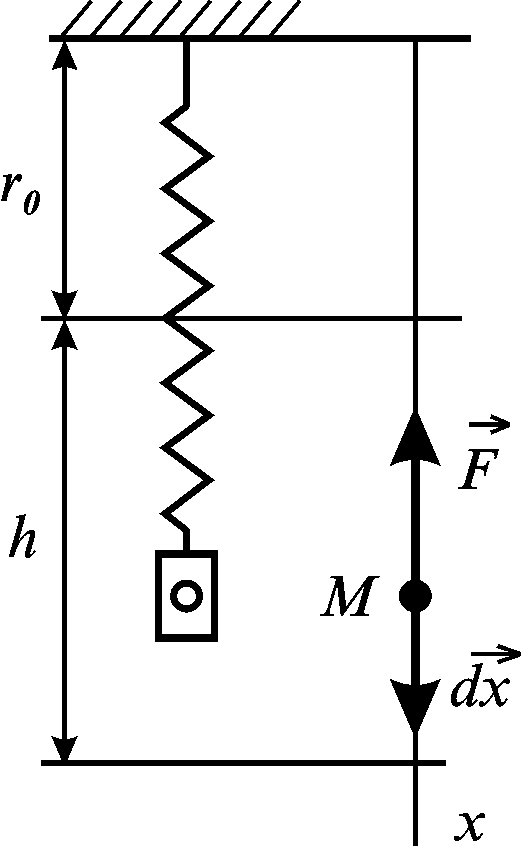
Рисунок 3.26

Нехай кінцева деформація пружини дорівнює . Повна робота

. (3.105)

Цей самий результат можна дістати із формули (3.104), якщо взяти .

Приклад 3.7. Нарешті, обчислимо роботу сталої за модулем і напрямом сили, що діє на точку, яка рухається прямолінійно (рис. 3.27). Точка О – початок відліку дугової координати . Згідно з (3.97)

.

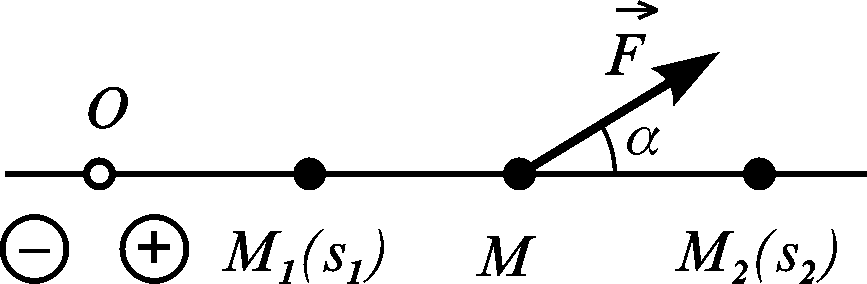
Рисунок 3.27

Повна робота

.

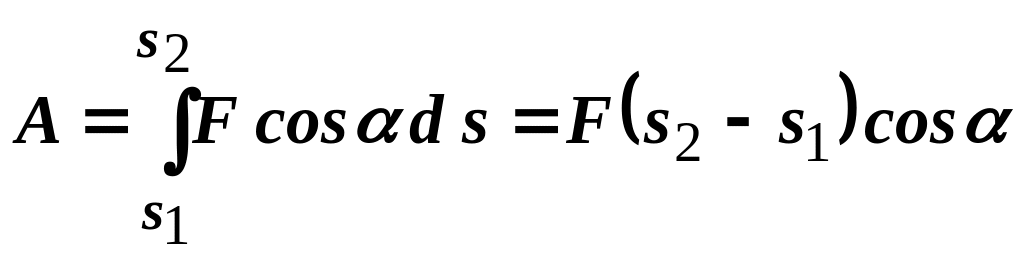3.3.2. Елементи теорії потенціального силового поля. Закон збереження повної механічної енергії

Силовим полем називають частину простору, в якому на матеріальну точку діє сила, що є однозначною функцією координат точки.

Інколи сила у силовому колі може залежати від часу, але ніколи — від швидкостей та прискорень.

Якщо час до виразу сили явно не входить, то поле називають стаціонарним.

Силове поле називають потенціальним при виконанні двох умов:

а) поле стаціонарне;

б) робота, яку виконують сили потенціального поля, не залежить від форми траєкторії точки, а залежить лише від координат її початкового та кінцевого положень.

Згадані раніше сили ваги, центральні сили, зокрема пружні, утворюють потенціальне силове поле.

Властивості такого поля можна описати за допомогою однієї скалярної функції координат, яку називають силовою функцією.

Нехай матеріальна точка починає рух з початку координат О (рис. 3.28). Обчислимо роботу, яку виконують сили поля, якщо точка переходить із точки О в довільну точку М поля. Ця робота не залежить від форми траєкторії, а є функцією координат кінцевої точки М.

Кожній точці М простору (поля) поставимо у відповідність цю роботу

де — силова функція.

Розглянемо довільну точку поля і обчислимо роботу, яку виконують сили поля при переході матеріальної точки з М в . На підставі означень потенціального поля маємо

,

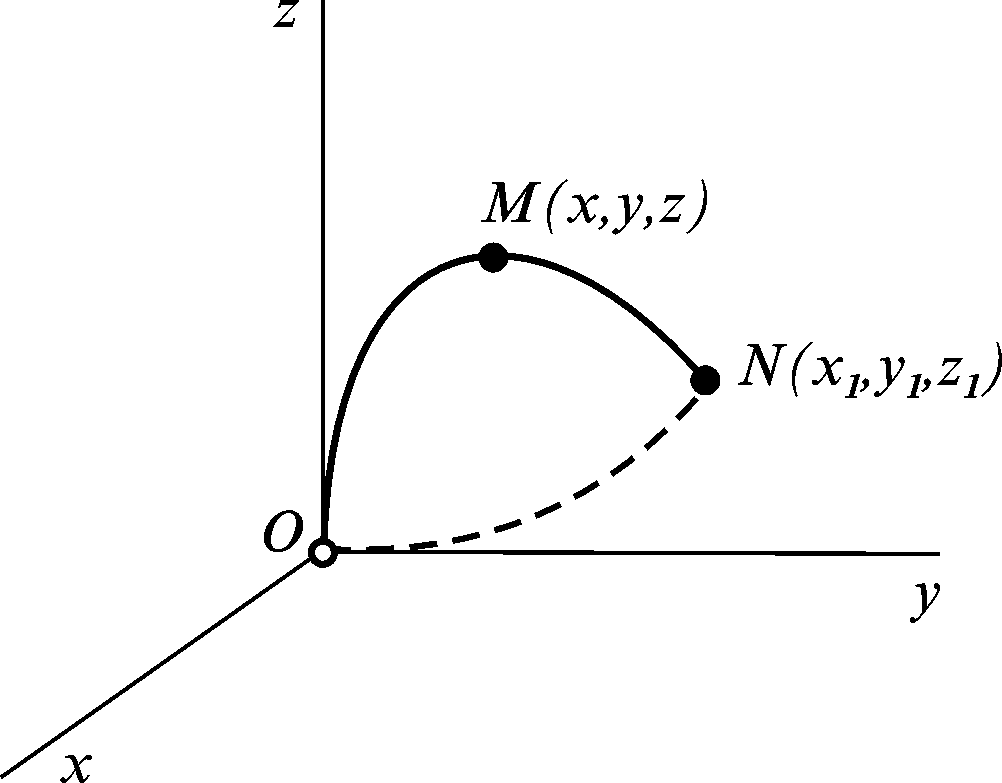
Рисунок 3.28

звідки

.

Отже, робота дорівнює приросту силової функції у відповідних точках поля.

Елементарна робота

, (3.106)

тобто,

в потенціальному силовому полі елементарна робота є повним диференціалом силової функції.

Порівнюючи (3.106) і (3.95), дістаємо формули, за якими

проекції сили на осі координат дорівнюють частинним похідним за відповідними координатами від силової функції:

. (3.107)

На підставі виразу (3.106) можна визначити силову функцію, якщо відомі сили поля:

, (3.108)

де – невизначена стала; – обчислюється за формулами (3.92), (3.95) або (3.97).

Якщо обчислити змішані похідні функції , то на підставі (3.107) дістанемо співвідношення

, (3.109)

які є необхідними умовами існування потенціального силового поля.

Достатність їх в однозв’язній області для однозначної силової функції випливає з формули Стокса.

Еквіпотенціальною поверхнею називають геометричне місце точок поля, де силова функція набуває певного сталого значення. Рівняння цієї поверхні має вигляд

. (3.110)

Якщо стала дорівнює нулеві, то поверхня проходить через початок координат і називається нульовою еквіпотенціальною поверхнею.

Із формули (3.108) випливає, що за нульову можна взяти будь-яку поверхню, підібравши відповідно сталу (рис. 3.29)

а	б
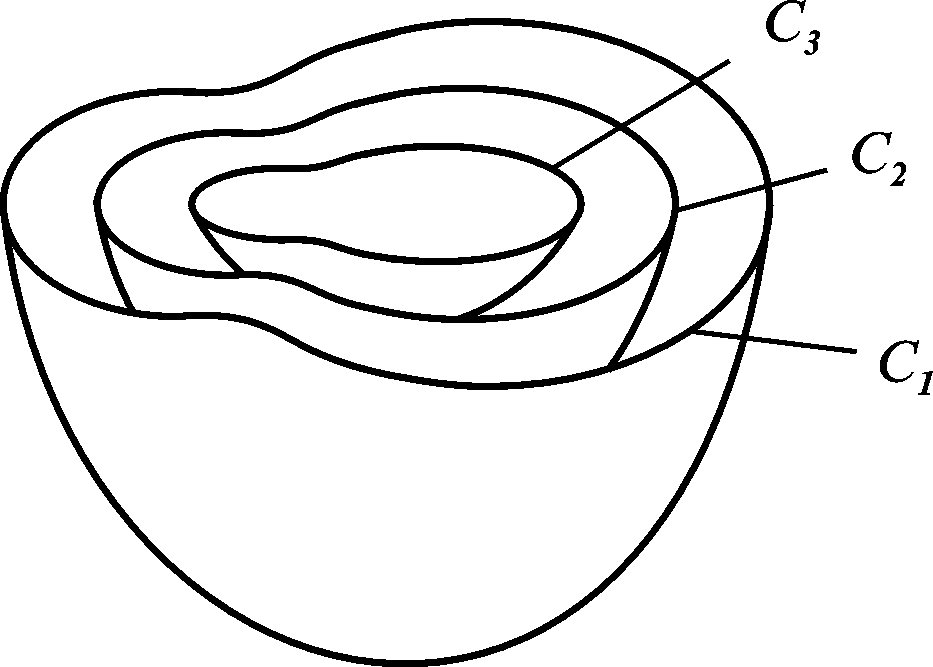
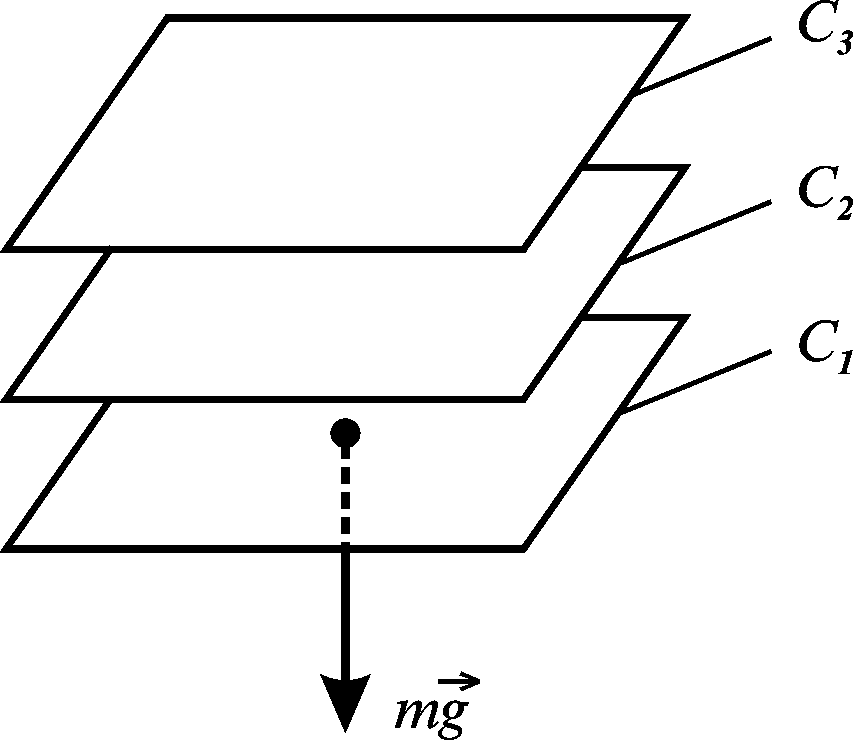
Рисунок 3.29

Повертаючись до означення силової функції, зазначимо, що робота сил поля при переході матеріальної точки з початку координат О в певну точку М дорівнює роботі сил при переході точки з довільної точки нульової еквіпотенціальної поверхні в точку М, оскільки силова функція дорівнює нулеві у будь-якій точці нульової еквіпотенціальної поверхні.

Тому можна узагальнити поняття силової функції:

силова функція дорівнює роботі, яку виконують сили, прикладені до точки в потенціальному полі, при переході точки з нульової еквіпотенціальної поверхні в певну точку М поля.

Зауважимо, що вектор сили завжди напрямлений перпендикулярно до еквіпотенціальної поверхні.

Розглянемо теорему про зміну кінетичної енергії точки (3.94) щодо потенціального силового поля

,

або

. (3.111)

Оскільки точки 1 і 2 взято довільно, то права і ліва частини (3.111) сталі скрізь, тобто

.

Згідно із загальним законом зміни енергії, складова ( ) також є певною енергією. Її називають потенціальною енергією точки і позначають через . Отже,

. (3.112)

Тоді

(3.113)

Суму кінетичної і потенціальної енергії точки називають повною механічною енергією.

Таким чином, на підставі (3.113) твердимо, що

при русі точки в потенціальному силовому полі повна механічна енергія зберігається.

Тому потенціальне силове поле є консервативним.

Сформульоване твердження називають законом збереження повної механічної енергії, а рівність (3.113) – один з перших інтегралів диференціальних рівнянь руху точки – інтегралом енергії. Це окремий випадок закону збереження речовини й енергії М.В.Ломоносова.

Згідно з (3.112)

потенціальну енергію визначають як роботу, яку виконують сили поля, прикладені до точки, при її переміщенні з певної еквіпотенціальної поверхні на нульову.

Відповідно до (3.107) і (3.112) проекції сили в потенціальному полі

. (3.114)

Для системи матеріальних точок та залежать від 3 координат точок:

. (3.115)

Проекції сил

.(3.116)