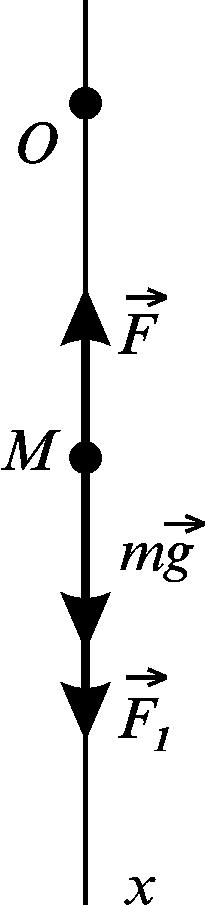3.1.2. Прямолінійні коливання точки

Рух, про який мова йтиме нижче, дуже поширений у різних механічних системах. Ми досліджуватимемо його, розглядаючи як ілюстрацію до другої задачі динаміки.

На основі енергетичного балансу коливання матеріальної точки розрізняють: вільні, згасаючі та вимушені.

Розглянемо рух тіла М (рис. 3.4), підвішеного до пружини. Якщо його вивести з положення рівноваги, то тіло рухатиметься зворотно-поступально.

Рисунок 3.4

Задачу розв’язуємо за таких припущень:

1) оскільки рух тіла поступальний, то його можна розглядати як матеріальну точку, що рухається по прямій;

2) масою пружини нехтуємо порівняно з масою тягара;

3) властивість матеріалу, з якого виготовлена пружина, задовольняє закон Гука.

Траєкторією точки М є вертикальна пряма, що збігається з віссю пружини. Користуючись координатним способом опису руху, проведемо вісь вертикально вниз. Початок координат виберемо у точці О, де буде знаходитися матеріальна точка, якщо її вага зрівноважується пружною силою . Цю точку називають положенням статичної рівноваги; відстань від точки О до , в якій знаходився кінець недеформованої пружини, дорівнює

, (3.20)

де – коефіцієнт жорсткості пружини; – маса точки.

Нехай точка М займає довільне положення після початку руху. Аналізуємо сили, прикладені до точки М: сила ваги , пружна сила і, якщо тіло рухається не у вакуумі, то опір середовища .

Згідно з законом Гука пружна сила пропорційна деформації пружини:

. (3.21)

Складова пружної сили намагається повернути тіло в положення статичної рівноваги, тому її називають поновлюючою силою.

Якщо швидкість точки порівняно мала, то сила опору в’язкого середовища пропорційна швидкості і напрямлена в бік, протилежний напряму швидкості:

, (3.22)

де – сталий коефіцієнт, який визначають з дослідів.

Складаємо рівняння руху точки:

.

Оскільки

,

то після деяких спрощень маємо

, (3.23)

де .

Рівняння (3.23) є однорідним диференціальним рівнянням зі сталими коефіцієнтами.

Складаємо характеристичне рівняння

.

Його корені

(3.24)

дають змогу розглянути три окремі випадки:

1) ; корені дійсні й різні. Загальний розв’язок рівняння (3.23)

(3.25)

містить неперіодичні функції і Внаслідок від’ємних значень відхилення точки від положення статичної рівноваги прямує до нуля зі зростанням часу .

Рух точки аперіодичний, бо відбувається при великих силах опору в’язкого середовища;

2) ; корені дійсні й рівні. Загальний розв’язок

. (3.26)

Рух точки також неперіодичний. Це є граничний випадок;

3) ; корені комплексні, і загальний розв’язок рівняння (3.23) містить періодичні функції:

. (3.27)

Рух точки називають згасаючими коливаннями.

Якщо змінити сталі інтегрування за формулами

де – нові сталі, причому

, (3.28)

то закон руху (3.27) матиме вигляд

. (3.29)

Множник є змінною амплітудою згасаючих коливань, яка прямує до нуля за експоненціальним законом зі зростанням часу .

І хоча з (3.29) не є цілком періодичною функцією, рух точки все ж має коливальний характер.

Зобразимо коло радіусом А (рис. 3.5) і проведемо вісь вертикально вгору. Розглянемо рух зображуючої точки з кутовою швидкістю з початкового положення (при = 0); – початкова фаза.

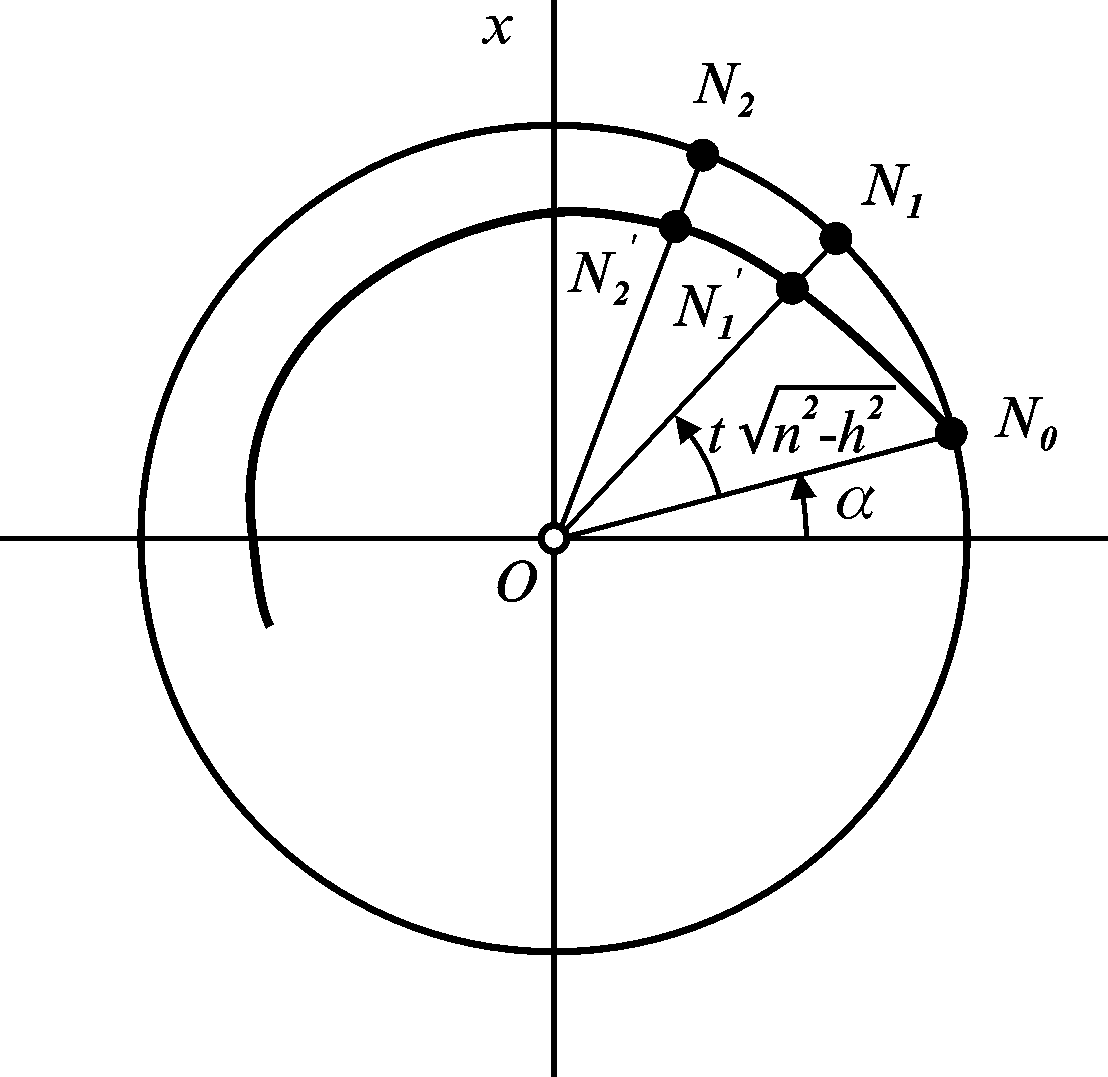
Рисунок 3.5

Кожному положенню точки ставимо у відповідність положення точки , радіус-вектор якої змінюється за законом . Рухові точки по колу відповідає рух точки по спіралі, а рух проекції точки на вісь описується законом (3.29), тобто здійснюються згасаючі коливання.

Величину називають циклічною частотою згасаючих коливань.

Періодом згасаючих коливань (це визначення досить умовне) називають проміжок часу між двома послідовними проходженнями точки через положення статичної рівноваги в певному фіксованому напрямі.

Зрозуміло, що періоду відповідає зміна аргументу синуса у виразі (3.29) на радіан:

,

звідки

. (3.30)

Згідно з (3.30) період не залежить від часу.

Зобразимо графік згасаючих коливань (рис. 3.6), тобто графік функції, яка відповідає (3.29). Спочатку накреслимо дві криві , які називають амплітудними кривими. На них синус дістає значення 1, і вони асимптично прагнуть до осі . Між ними розміщено графік згасаючих коливань. З кожним розмахом відхилення точки від положення рівноваги зменшується. Модулі відхилень мають такі значення:

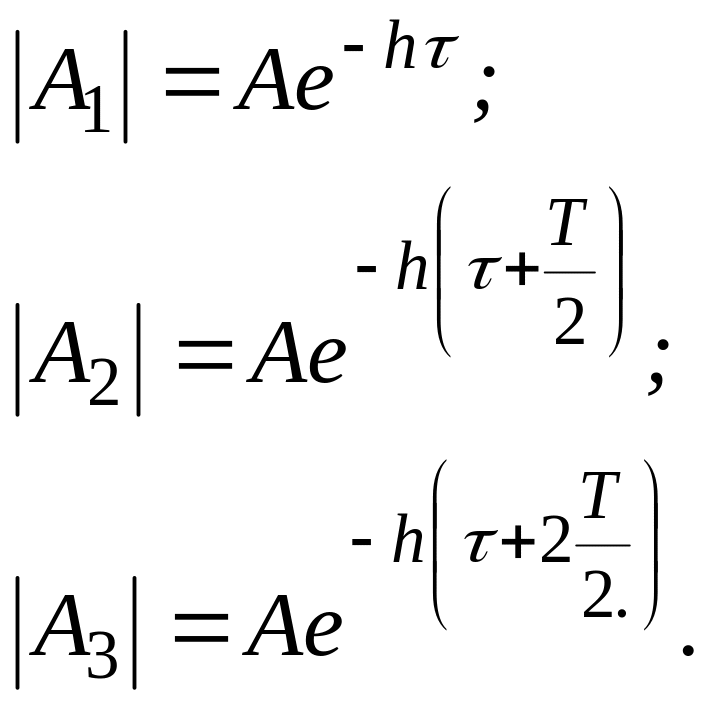
Ця послідовність є спадною геометричною прогресією із знаменником

.

Величину називають декрементом коливань; вона характеризує швидкість згасання коливань:

. (3.31)

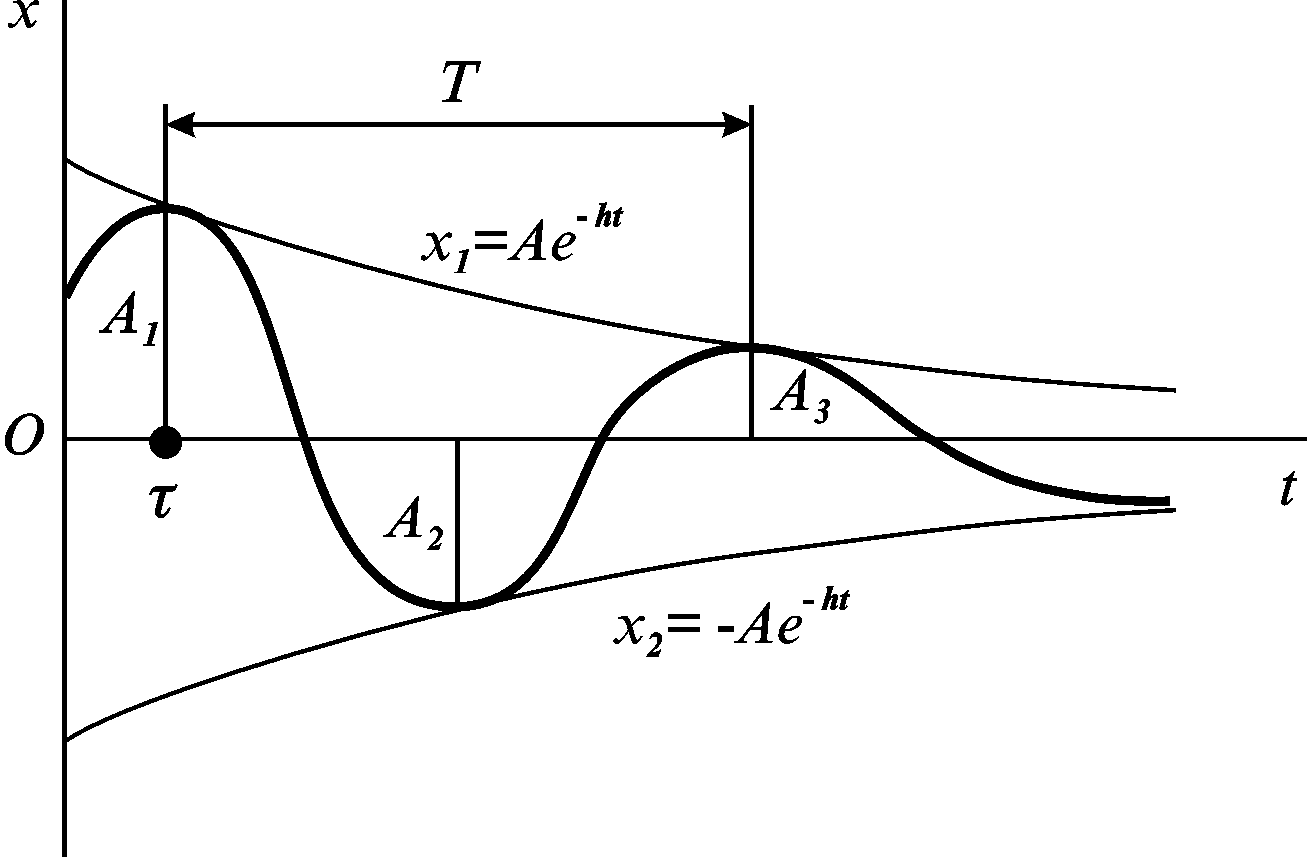
Рисунок 3.6

Натуральний логарифм величини називають логарифмічним декрементом

. (3.32)

Це поняття дає змогу експериментально знайти коефіцієнт опору середовища у виразі (3.22).

Для більш поглибленого ознайомлення з розглянутими питаннями радимо звернутися до підручників, вказаних у списку літератури.

Наприкінці зауважимо, що сталі у виразі (3.27) знаходимо з початкових умов:

(3.33)

Диференціюючи (3.27) за часом, знаходимо

. (3.34)

На підставі (3.33) з (3.27) і (3.34) маємо

. (3.35)

Враховуючи (3.28) і (3.35), можна знайти також сталі .

Частинний випадок розглянутих коливань – вільні незгасаючі коливання, коли , при цьому , і рівняння руху (3.23) набуде вигляду

. (3.36)

Закон руху точки :

, (3.37)

або

, (3.38)

де число називають циклічною частотою вільних коливань.

Період вільних коливань

, (3.39)

або

, (3.40)

оскільки

.

Формула (3.40) дає змогу знайти період коливань не тільки в задачі про коливання тягаря на пружині в порожнині, а також у цілому класі задач, оскільки пружина тут є тільки джерелом пружної сили. Такими тілами можуть бути пружні балки, стержні, тощо. Якщо статичний прогин у цих випадках відомий, то завжди можна знайти період їх вільних коливань.

Вільні коливання практично завжди згасаючі. Якщо необхідно створити незгасаючі коливання, до системи обов’яз-ково треба підводити енергію ззовні. Виникаючі внаслідок цього коливання називають вимушеними, а сили, які викликають вимушені коливання, називають збурювальними силами. Походження цих сил дуже різноманітне. Приклади можна знайти у повніших підручниках.

Н

Рисунок 3.7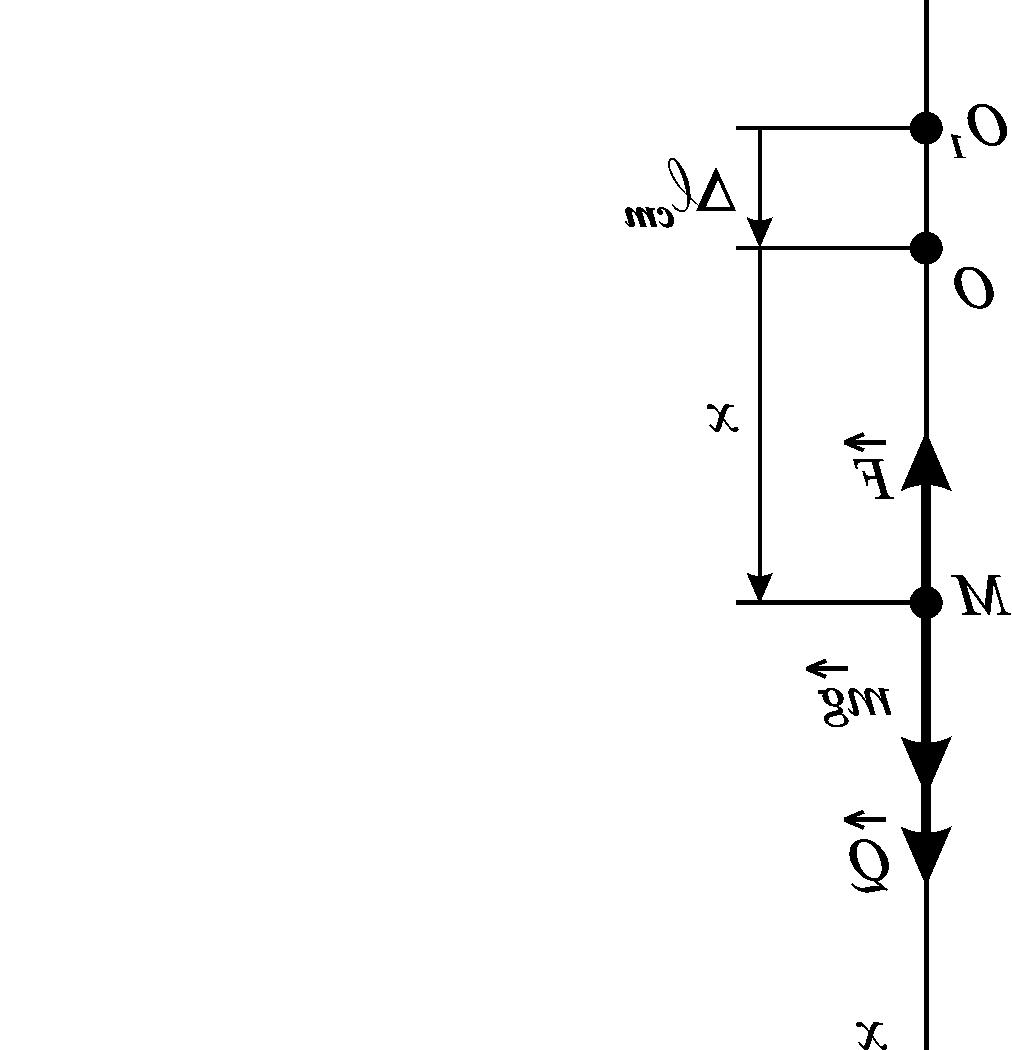

айчастіше збурювальні сили є функціями часу, і насамперед періодичними функціями, бо їх викликає незрівноважений рух двигунів, які входять до інженерних конструкцій.

Припустимо, що збурювальна сила є періодичною і виражається однією гармонікою

, (3.41)

Якщо сила змінюється за складнішим законом, то її можна розкласти в ряд Фур’є, один із членів якого є (3.41).

Розглянемо випадок, коли опір середовища дуже малий і ним нехтуємо. Відповідно до рис. 3.7, складемо диференціальне рівняння руху:

.

Оскільки початок координат збігається з положенням статичної рівноваги, то , а рівняння набуває вигляду

, (3.42)

де

.

Загальний розв’язок рівняння (3.42) складається із загального розв’язку (3.37) відповідного однорідного рівняння і частинного розв’язку рівняння (3.42):

, (3.43)

де А — невизначена стала.

Підставляючи (3.43) у (3.42), дістаємо рівняння для визначення А:

(3.44)

Значення сталої А дістаємо за умови, що , оскільки це відповідає випадкові . Отже,

. (3.45)

Розв’язок (3.43) та загальний розв’язок рівняння (3.42) відповідно мають вигляд

;

. (3.46)

Нехай у початковий момент

.

Диференціюючи (3.46) за часом, маємо

. (3.47)

Із (3.47) і (3.46) на підставі початкових умов знаходимо

.

Після підстановки значень в (3.46) матимемо

. (3.48)

Отже, коливання точки А складається з:

а) вільних коливань

,

які мають частоту вільних коливань і не залежать від амплітуди Н збурювальної сили, а залежать від початкових умов;

б) коливань

,

які мають частоту вільних, але не залежать від початкових умов; крім того, вони зникають при , тому вони – вимушені;

в) вимушених коливань

,

які мають частоту збурювальної сили і не залежать від початкових умов. Отже, якщо потрібно знайти тільки вимушені коливання, то треба шукати саме частинний розв’язок (3.43) рівняння (3.42).

Зрозуміло, що при зменшенні різниці амплітуда вимушених коливань зростає, а це може спричинити руйнування споруд. Тому вкрай важливо дослідити випадок збігання частоти вільних коливань системи з частотою збурювальної сили.

Розглянемо вимушені коливання і знайдемо при границю двох останніх доданків (3.48), які позначимо через :

.

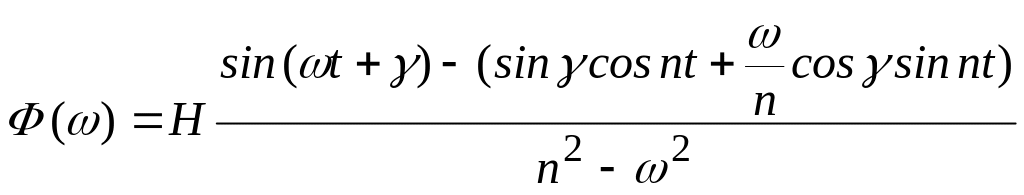Скористаємося правилом Лопіталя, оскільки цей вираз має невизначеність типу при :

.

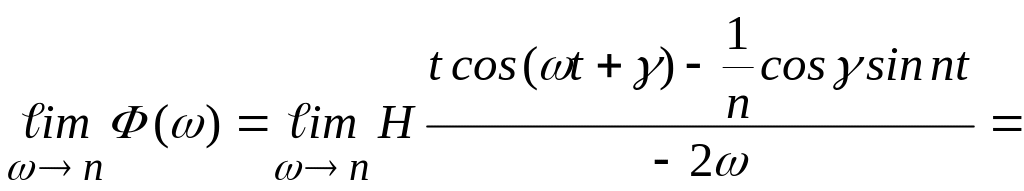
Таким чином, розв’язок (3.48) при набуває вигляду

.(3.49)

Цей випадок називають резонансом.

Останній член у (3.49) — закон вимушених коливань при резонансі. Амплітуда коливань зростає прямо пропорційно часу, тобто не має обмежень (рис. 3.8).

Рисунок 3.8

Рисунок 3.9

Зазвичай наявність сил опору не дає змоги амплітуді вимушених коливань зростати необмежено, але й тут випадок резонансу дуже небезпечний для конструкцій, бо амплітуда коливань може досягти великих значень навіть при наявності опору. Приклад 3.1. Тягар вагою 2,45 Н висить на пружині, коефіцієнт жорсткості якої с = 100 Н/м. На тягар діє вертикальна сила (Н). Знайти закон руху тягаря. Віднесемо рух точки до осі, напрямленої вертикально вниз (рис. 3.9) (початок осі знаходиться у положенні статичної рівноваги). На точку діють сила ваги = 2,45 Н, пружна сила і збурювальна сила (Н). Складаємо диференціальне рівняння руху

Спростимо його, оскільки , та поділимо на :

. (3.50)

Загальний розв’язок рівняння (3.50) складається із загального розв’язку

(3.51)

однорідного рівняння і частинного розв’язку рівняння (3.50) у формі

;

оскільки тут рад/с; = 16 рад/с; , то з (3.45)

= 0,05 м.

Загальний розв’язок рівняння (3.50) має вигляд

. (3.52)

Диференціюючи цей вираз, знаходимо

. (3.53)

Оскільки в початковий момент часу тягар висів на пружині нерухомо, то . Підставляючи ці значення у (3.52) і (3.53) знайдемо:

м.

Розв’язок (3.52) набуває вигляду

(м).