3.3.4. Обчислення моментів інерції

В усіх випадках руху системи або твердого тіла, крім поступального, при обчисленні кінетичної енергії треба знати їх моменти інерції.

Спочатку з’ясуємо зв’язок між моментами інерції тіла (системи) відносно паралельних осей.

Для цього розглянемо два вирази кінетичної енергії тіла при плоскопаралельному русі. Один з них — це формула (3.127), а другий дістанемо як кінетичну енергію миттєвого обертального руху тіла навколо миттєвого центру швидкостей (миттєвої осі обертання )

, (3.137)

де — момент інерції тіла відносно осі, яка проходить паралельно центральній через миттєвий центр обертання.

Порівнюючи вирази (3.127) і (3.137) і беручи до уваги, що

,

де — відстань між осями, тобто між центром мас і миттєвим центром швидкостей, дістанемо

.

Скорочуючи на , дістанемо

. (3.138)

Ця рівність свідчить, що

момент інерції тіла (системи) відносно довільної осі дорівнює сумі моменту інерції тіла відносно паралельної осі, що проходить через центр мас тіла (центральної осі), і добутку маси тіла на квадрат відстані між осями.

Наведене твердження називають теоремою Штейнера.

Введемо поняття про радіус інерції тіла.

Радіусом інерції тіла (системи) відносно певної осі називають ту відстань від осі, на яку треба віднести зосереджену у точці масу, рівну масі тіла, щоб момент інерції цієї точки відносно осі дорівнював моменту інерції тіла.

Отже, згідно з означенням,

,

звідки

. (3.139)

На підставі формул (3.139) і (3.138) робимо висновок, що радіус інерції відносно центральної осі найкоротший.

Для знаходження формули, яка дасть змогу обчислити момент інерції тіла відносно довільної осі, яка проходить через початок координат, порівняємо вираз (3.124) і другий член (3.128), узявши до уваги, що

, (3.140)

де — відповідно кути, які утворює з осями координат напрям вектора миттєвої кутової швидкості .

Скоротивши порівнювані вирази на , дістанемо

(3.141)

.

Візьмемо на осі точку (рис. 3.31), причому

.

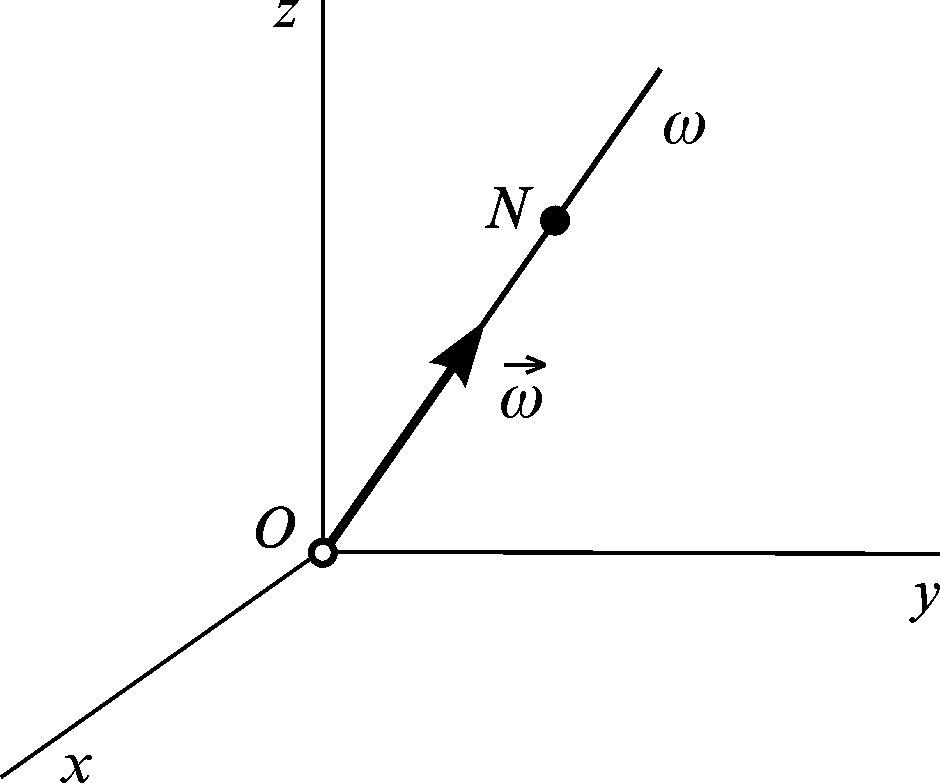
Рисунок 3.31

Помножимо обидві частини виразу (3.141) на і, взявши до уваги, що координати точки задовольняють рівностям

, ,

дістанемо рівняння поверхні другого порядку

, (3.142)

якою рухається точка , якщо змінюється напрям осі .

Указана множина точок є поверхнею еліпсоїда, оскільки відстань скінченна ( ).

Цей еліпсоїд називають еліпсоїдом інерції.

Його осі симетрії називають головними осями інерції для тієї точки тіла, в якій побудовано еліпсоїд інерції; напрями головних осей — головними напрямами, а моменти інерції відносно головних осей — головними моментами інерції.

Якщо переходити від однієї точки тіла до іншої, то напрями головних осей змінюються.

Якщо осі координат є осями симетрії еліпсоїда, то рівняння поверхні (3.142) набуває канонічної форми

,

тобто

відцентрові моменти інерції відносно головних осей дорівнюють нулеві.

Сформулюємо без доведення дві теореми.

Теорема 1. Якщо однорідне тіло має площину симетрії, то вісь, перпендикулярна до цієї площини, є головною віссю інерції тіла для точки перетину її з площиною.

Теорема 2. Якщо однорідне тіло має вісь симетрії, то ця вісь для кожної її точки є головною віссю інерції.

Наведемо вирази моментів інерції тіл простішої форми.

1. Момент інерції однорідного стержня довжиною відносно осі , яка проходить через його кінець перпендикулярно до нього,

, (3.143)

де — маса стержня.

2. Момент інерції однорідного прямого кругового циліндра масою відносно осі симетрії , яка перпендикулярна до його основи,

, (3.144)

де – радіус циліндра.

Якщо циліндр порожнистий, то

. (3.145)

Приклад 3.8. Через блок А вагою (рис. 3.32) перекинуто нерозтяжний невагомий трос, до одного кінця якого прикріплено вісь колеса В тим самим радіусом та вагою, а до другого кінця — тягар С вагою Р, який починає рухатися зі стану спокою, обертає блок і змушує колесо В котитися без ковзання. Маси блока А та колеса В розподілені по їхніх обводах рівномірно. Нехтуючи тертям на осі, знайти швидкість тягаря С (залежно від пройденого ним шляху ) та його прискорення а.

Рисунок 3.32

Скористаємося теоремою про зміну кінетичної енергії системи, оскільки треба відшукати швидкість тіла залежно від його переміщення . Маємо

, (3.146)

де , тому що в початковий момент система була в спокої.

Система складається з трьох тіл. Отже,

.

Тягар С рухається поступально, тому

.

Блок А обертається навколо нерухомої осі. Тому

(оскільки , а ).

Колесо В здійснює плоскопаралельний рух, тому

.

(оскільки швидкість його центра мас О дорівнює ; а ).

Складаючи всі вирази, знаходимо

. (3.147)

Робота сил складається з роботи сил ваги, прикладених у центрах мас тіл, та роботи реакцій в’язей: і – складових реакцій нерухомої осі блока А і нормальної реакції поверхні та сили тертя у точці дотику колеса В до площини.

Робота внутрішніх сил системи дорівнює нулеві, оскільки система незмінна.

Сила ваги блока, реакції і прикладені в нерухомій точці, тому їх робота дорівнює нулеві. Центр О колеса В рухається горизонтально, тому робота сили ваги колеса дорівнює нулеві. Нормальна реакція і сила тертя площини прикладені до миттєвого центра швидкостей колеса, тобто до миттєвої нерухомої точки. Тому їх робота також дорівнює нулеві.

Отже, робота сил дорівнює лише роботі сили ваги тягаря:

. (3.148)

Підставляючи (3.148) і (3.147) у рівність (3.146), знаходимо

. (3.149)

Рух тягара під дією сталих сил відбувається рівноприскорено, тому, порівнюючи вираз (3.149) з відомою формулою , знайдемо

.