3.2.2. Диференціальні рівняння руху невільної системи

Для того, щоб дослідити рух невільної матеріальної системи, потрібно скласти диференціальні рівняння її руху. Другий закон І.Ньютона дає змогу скласти рівняння руху тільки для вільної системи, тому насамперед систему треба звільнити від в’язей на підставі відповідної аксіоми.

Розглянемо точку , до якої прикладені – рівнодійна активних сил і – рівнодійна реакцій в’язей. Якщо скористатися координатним способом, то диференціальні рівняння руху точки матимуть вигляд

(3.66)

де – суми проекцій активних сил; – суми проекцій на осі координат реакцій в’язей, які діють на точку .

Система (3.66) складається з рівнянь і містить невідомих ( координат і проекцій рівнодійної реакцій в’язей), тобто невідомих вдвічі більше, ніж рівнянь.

Припустимо, що на систему накладено в’язей типу (3.58), тобто рівнянь буде , але ця кількість менша за , оскільки при русі системи обов’язково .

Це свідчить про те, що розв’язати у загальному випадку задачу про рух невільної системи методами лише теоретичної механіки, не вдаючись до припущень відносно властивостей в’язей, неможливо.

Але якщо в’язі ідеальні, тобто (див. підрозд. 1.1.3) такі, що лінії дії їхніх реакцій відомі, то невідомих серед реакцій в’язей буде не , а лише модулів реакцій, а напрями (вірніше їхні лінії дії) будуть відомі.

Отже, маємо рівнянь, які містять невідомих, тобто задачу, в принципі, можна розв’язати.

Якщо в’язі неідеальні, треба брати до уваги певні співвідношення, які враховують фізичні властивості в’язей. Наприклад, якщо площина шорстка, потрібно врахувати властивості сил тертя ковзання.

Труднощі, які виникають при розв’язанні другої задачі динаміки невільної системи, пов’язані ще й з тим, що разом з визначенням координат точок як функцій часу треба знаходити невідомі реакції в’язей.

В аналітичній механіці буде показано, що ці дві задачі можна розв’язувати окремо, якщо вибирати координати спеціальним способом так, як указав Ж.Лагранк у ХVШ ст.

3.2.3. Принцип Даламбера

У ХVШ ст. розвиток техніки призвів до необхідності розв’язувати задачі руху невільних систем. Перші кроки на цьому шляху зробили вчені Я.Герман і Л.Ейлер. Вони знайшли принцип, за допомогою якого стало можливим вивчати невільні системи. Вчені ХVШ ст. навіть називали його петербурзьким принципом, тому що на той час Герман і Ейлер були членами Петербурзької АН.

Але широко принцип було впроваджено лише після робіт Даламбера, який на прикладах навчив ним користуватися. Тому остаточно принцип дістав назву принципу Даламбера. Пояснимо його суть.

Припустимо, що невільна матеріальна точка М рухається по заданій кривій (рис. 3.11) під дією сили – рівнодійної активних сил і – рівнодійної реакцій в’язей. На підставі аксіоми про паралелограм сил додамо їх: – векторна сума сил і , прикладених до точки М. Маємо векторне рівняння руху точки:

. (3.67)

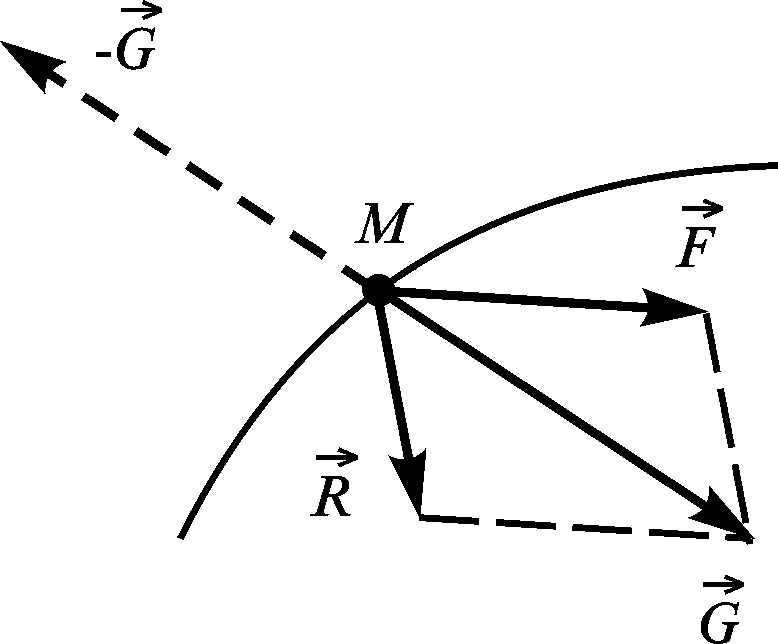
Рисунок 3.11

Але якщо певні тіла діють на точку із силами і , то за третім законом І.Ньютона матеріальна точка діє на ці самі тіла з силою, рівнодійна яких дорівнює , але напрямлена у протилежний бік (на рис. 3.11 її зображено штрихами).

Сила (- ) до точки М не прикладена. Це – сила протидії точки М тим тілам, які викликають її прискорення та реакції в’язей.

Перенесемо всі доданки рівняння (3.67) в одну частину рівності:

. (3.68)

Оскільки векторна сума сил дорівнює нулеві, то маємо умову рівноваги точки, але ця рівновага не “справжня”, тому що перші дві сили ( і ) прикладені до точки М, а сила (- ), яка дорівнює (- ), до точки не прикладена.

Силу ( ) називають силою інерції і позначають

. (3.69)

Сила інерції дорівнює добутку маси на прискорення. Вона напрямлена в бік, протилежний прискоренню точки.

Це є головний вектор сил протидії, прикладених до зовнішніх тіл, одні з яких є джерелами активних сил, інші – в’язями, тому в природі існують реально тільки її складові, прикладені до різних тіл. Лише тоді, коли точка взаємодіє з одним тілом, головний вектор сил інерції фізично існує у вигляді однієї сили.

Рівність (3.69) називають принципом Даламбера:

активні сили і реакції в’язей, прикладені до точки, “зрівноважуються” силою інерції.

Слово “зрівноважуються” взято в лапки тому, що насправді точка має прискорення, а не перебуває в рівновазі.

Значення принципу Даламбера полягає в тому, що він дає змогу складати рівняння руху невільної системи у формі рівнянь рівноваги. Його найефективніше застосовувати при розв’язанні першої задачі динаміки, тобто тоді, коли невідомими є сили.

Зрозуміло, що принцип Даламбера не допомагає подолати основні труднощі при розв’язанні другої задачі динаміки, пов’язані з інтегруванням рівнянь руху.

Поширимо принцип Даламбера на рух системи точок і абсолютно твердого тіла.

Якщо йдеться про рух системи точок, то рівність (3.68) можна застосувати при дослідженні руху кожної точки системи, тобто

. (3.70)

Рівняння (3.70) є математичним виразом принципу Даламбера для системи точок.

Абсолютно тверде тіло можна розглядати як окремий випадок системи точок. Тоді для тіла справедливі вирази (3.70). Додамо їх почленно:

. (3.71)

Перший доданок у (3.71) є головним вектором усіх активних сил , другий – головним вектором реакцій в’язей , третій – головним вектором сил інерції . Отже,

. (3.72)

Виберемо довільний центр О і проведемо з нього радіус-вектор в точку . Помножимо кожне рівняння (3.70) зліва векторно на і додамо почленно:

. (3.73)

Перша сума в (3.73) – головний момент усіх активних сил відносно точки О, друга – головний момент реакцій в’язей , третя – головний момент сил інерції .

Отже,

. (3.74)

Таким чином,

якщо до тіла прикласти сили інерції і розглядати всі сили – активні, реакції в’язей і сили інерції – як єдину систему сил, прикладених до тіла, то головний вектор і головний момент цих сил дорівнюють нулеві.

Отже, принцип Даламбера дає змогу запровадити особливу методику розв’язування задач динаміки, яка полягає у застосуванні в динамічних задачах рівнянь рівноваги статики.

Аналогії між статикою і динамікою показано у табл. 3.1.

Таблиця 3.1

Розділ механіки	Точка	Система точок	Абсолютно тверде тіло
Статика		,	;
Динаміка

Якщо прикласти до точки чи тіла сили, що дорівнюють силам інерції, то рівняння руху за формою збігається з рівняннями рівноваги.

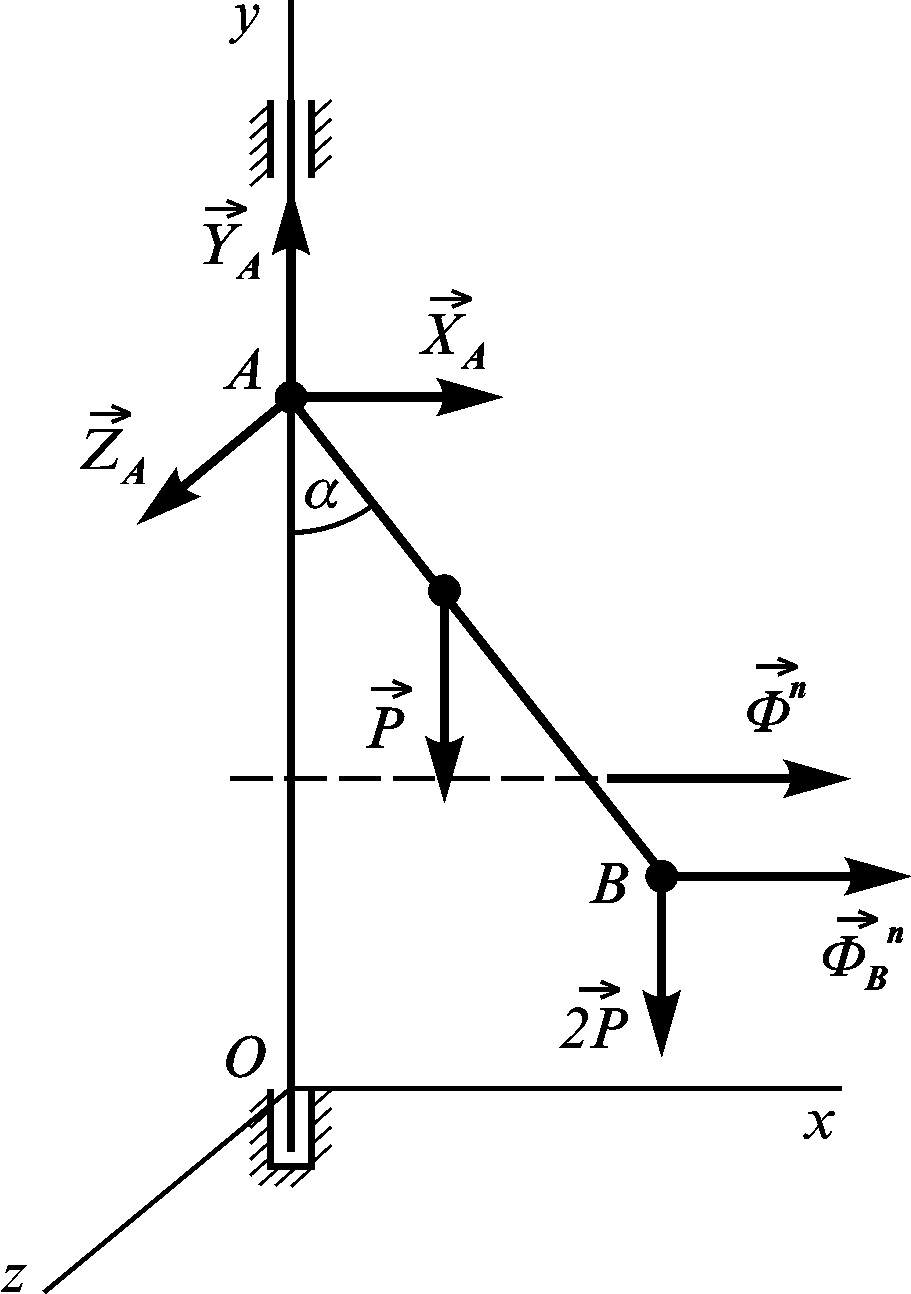
Приклад 3.2. Тонкий однорідний стержень АВ вагою Р і довжини (рис. 3.12, а) обертається навколо вертикальної осі зі сталою кутовою швидкістю . До кінця В стержня прикріплено точковий тягар вагою 2Р. Знайти реакції шарніра А.

а	б
Рисунок 3.12

Система складається з однорідного стержня і точки В. Активними силами є сили ваги і 2 ; сила прикладена в центрі ваги стержня (в його середині).

Звільнимося від в’язі – вертикального вала, який з’єднано зі стержнем АВ за допомогою шарніра А. Виходячи з найзагальніших припущень, вважаємо, що шарнір А – сферичний, тобто його реакцію розкладаємо на три складові:

.

При розв’язуванні задачі із застосуванням принципу Даламбера до системи прикладаємо сили інерції. При сталій кутовій швидкості всі точки стержня мають лише нормальні прискорення, які прямо пропорційні відстані точки від осі обертання. Той самий закон задовольняють і нормальні складові сил інерції. Сила інерції точкової маси В дорівнює добутку її маси на прискорення:

(3.75)

і напрямлена “від” осі .

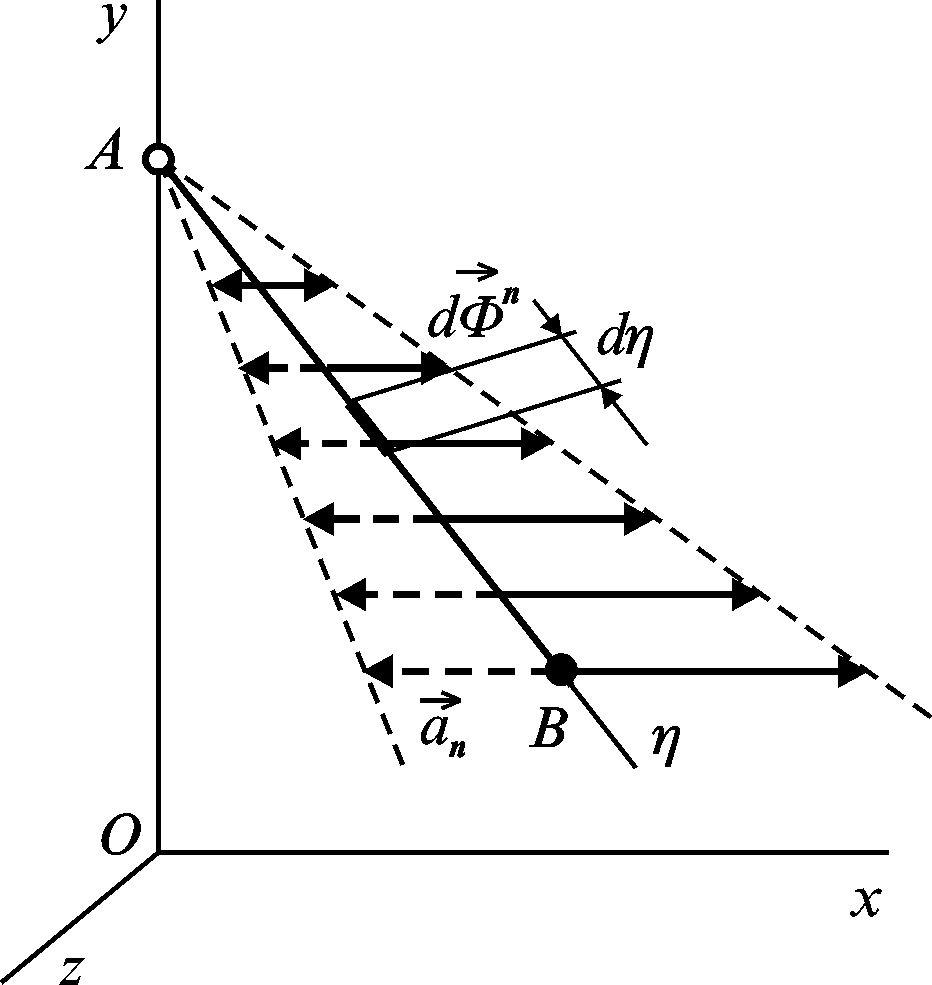
“Відцентрові” сили інерції розподілені вздовж стержня за законом трикутника. На рис. 3.12, б штриховими лініями показано епюри нормальних прискорень і суцільними лініями сил інерції.

Якщо взяти вісь вздовж стержня, то елементарна сила інерції, прикладена до часточки стержня довжиною ,

, (3.76)

де – елементарна маса.

Для відшукання рівнодійної сил інерції потрібно проінтегрувати вираз (3.76)

(3.77)

Лінія дії цієї сили горизонтальна і віддалена від точки А на , тобто проходить через центр “ваги” навантаження за рахунок розподілення сил інерції за законом трикутника.

Зауважимо, що сили інерції тільки умовно прикладені до системи. Насправді вони діють з боку системи (стержня АВ і точки В) на тіла, які взаємодіють із системою, і, насамперед, на шарнір А. Тому в цьому шарнірі виникають додаткові реакції, які називають динамічними.

Умовне прикладення сил інерції немов “зупинило” систему, і тепер можна складати умови рівноваги за принципом Даламбера.

Система сил, яка прикладена до стержня, за винятком сили , лежить в площині . Тому робимо висновок, що . Плоска система сил має три умови рівноваги. Оскільки потрібно визначити і , складаємо спочатку рівняння, до яких входять суми проекцій сил на осі і :

, (3.78)

звідки

;

.

Але з умови задачі невідомим є кут . Тому складемо ще одне рівняння

,

звідки

. (3.79)

Примітка. Оскільки , то з виразу (3.79) випливає оцінка

,

тобто

.

Це свідчить, що вказаний у задачі рух може відбуватися тільки за цих значень кутової швидкості .

З виразу (3.79) знаходимо

і підставляємо його до значення . Остаточно дістаємо

.

Реакція шарніра А

.