2.1Постановка задачи оптимизации выпуска продукции

Задача распределения ресурсов для оптимизации ассортимента и выпуска продукции предприятием может быть поставлена следующим образом:

Предприятие выпускает несколько видов продукции. На производство единицы каждого вида продукции затрачиваются определенные количества заданного числа ресурсов. Известны цены на единицу каждого вида продукции. Требуется определить объем выпуска каждого вида продукции с тем, чтобы стоимость выпущенной продукции была максимальной.

Задача распределения ресурсов непосредственно в этой постановке решается методами линейного программирования, рассматривающего линейные функциональные зависимости между переменными. Ограничения задачи детерминированы, искомое решение непрерывно. Такие задачи называются задачами линейного программирования (ЗЛП).

Постановка общей ЗЛП:

Дана система из m неравенств, левые части которых есть некоторые линейные функции от n переменных. Существует некоторая линейная функция этих переменных, которая назначается на максимальное, минимальное значение или на величину, которая нас интересует. Требуется найти решение данной системы неравенств, при котором линейная функция достигает своего назначения.

Математическая модель имеет вид:

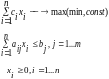
(2.1)

Общая ЗЛП может быть приведена к каноническому виду (системе уравнений, а не неравенств). Для этого к левой части каждого неравенства добавляется добавочная переменная у_j , равная разности между правой и левой частями неравенств.

Таким образом ЗЛП принимает вид

(2.2)

Это тождественное преобразование приводит систему неравенств к эквивалентной системе уравнений. Решение полученной системы уравнений называют допустимым решением ЗЛП или ее опорным планом. Допустимое решение, при котором целевая функция достигает своего назначения, называется оптимальным решением или оптимальным планом.

2.2Методы решения задачи оптимизации выпуска продукции

В случае, когда количество искомых переменных не превышает 3, ЗЛП можно решить графически. Графическое решение ЗЛП основано на следующих двух теоремах.

Теорема 1

Область допустимых решений ЗЛП есть выпуклое множество (выпуклый многогранник).

Теорема 2

Оптимальное решение ЗЛП достигается в одной из вершин области допустимых решений.

Графическое решение ЗЛП можно выполнить для случая двух переменных по следующему алгоритму.

Алгоритм графического решения ЗЛП:

1. Составляется задача в виде ЗЛП.

2. Строятся графики прямых, соответствующих ограничениям ЗЛП.

3. По ограничениям и граничным условиям строится область допустимых решений (ОДР).

4. Стоится прямая целевой функции, проходящая через начало координат (линия уровня). Уравнение прямой – целевая функция, приравненная к 0.

5. Линия уровня переносится в направлении перпендикуляра к ней (параллельно) во все вершины ОДР.

6. Определяется вершина, линия уровня в которой лежит выше всех других. Координаты этой точки и есть оптимальное решение ЗЛП. Их можно найти, решив систему уравнений соответствующих прямым, точкой пересечения которых является эта вершина.

Аналитическое решение ЗЛП

Как уже отмечалось выше, графическое решение удобно только для двумерных задач. Для решения ЗЛП без ограничения размерности применяется симплексный метод. Название метода связано с понятием симплекса – совокупности n+1 вершины в n-мерном пространстве.

Идея метода состоит в следующем: выбирается более или менее очевидное начальное решение исходной задачи. Далее осуществляется ряд последовательных шагов, сводящихся к элементарным алгебраическим операциям. При каждом шаге (итерации) получается новое решение задачи, которое не хуже предыдущего. Через конечное число шагов либо определяется, что решения не существует, либо находится оптимальное решение.

Переход от одного решения к другому, лучшему, представляет собой не что иное, как последовательный перебор точек симплекса (вершин ОДР). Направление перехода задается сменой базиса или выражением одних переменных через другие путем эквивалентного преобразования уравнений. Базисные переменные (в левой части равенств) выражаются через свободные с соответствующими коэффициентами (в правой части равенств). Соответственно при выражении базиса через свободные переменные меняется и вид целевой функции.

Симплексный метод может быть реализован аналитически – непосредственно преобразованиями уравнений и использованием симплекс-таблиц. Последний способ значительно удобнее и сводится к последовательному построению таблиц специального вида, значения в которых рассчитываются по определенным правилам.

Общий вид первоначальной симплекс-таблицы представлен на рис. 2.1.

Базисные переменные	Вектор свободных членов	Переменные ЗЛП
		x1	x2	. . .	xn	y1	y2	. . .	ym
y1	b1
y2	b2
………...	……..	……	……	……	……	…..	……	…..	.....
Индексы в целевой функции	0	c1	c2	. . .	cn	0	0	. . .	0

Рис. 2.1. Общий вид симплекс-таблицы

Алгоритм симплексного метода с применением симплекс-таблиц

1. Составляем общую ЗЛП по условиям задачи (2.1).

2. Приводим ЗЛП к каноническому виду (2.2).

3. З 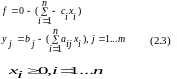аписываем задачу в виде 0-уравнений и выражаем базисные переменные через свободные.

4. Составляем первую симплексную таблицу.

5. Анализируем индексную строку: если все элементы индексной строки при решении задачи на максимизацию положительны (при решении задачи на минимизацию отрицательны), то полученное решение уже оптимально. Это решение получается приравниванием свободных переменных к 0 и столбца свободных членов для базисных переменных.

6. Если в индексной строке при решении задачи на максимизацию есть отрицательные значения (при решении задачи на минимизацию – положительные значения), то из них выбирается наибольшее по модулю. Выбранное значение определяет столбец нового базисного вектора – разрешающий столбец таблицы.

7. Для определения разрешающей строки составляются отношения значений столбца свободных членов к элементам разрешающего столбца. Строка, в которой это отношение наименьшее, есть разрешающая строка симплекс-таблицы. Базисная переменная этой строки при следующем шаге заменится на переменную разрешающего столбца.

8. Элемент таблицы, стоящий на пересечении разрешающей строки и разрешающего столбца, есть разрешающий элемент симплекс-таблицы.

9. Строим новую симплексную таблицу. В столбце базисных переменных переменная разрешающей строки заменяется на переменную разрешающего столбца.

10. Строка, соответствующая новому базисному вектору, получается из разрешающей строки предыдущей таблицы делением на разрешающий элемент.

11. Элементы других строк новой симплекс-таблицы, включая индексную строку, вычисляются следующим образом: значение элемента в предыдущей таблице минус дробь, числитель которой есть произведение значений, соответствующих вычисляемому элементу в разрешающей строке и разрешающем столбце предыдущей таблицы, а знаменатель – разрешающий элемент предыдущей таблицы.

12. Переходим к шагу 5.