3.8. Численное решение задачи Кощи для обыкновенного дифференциального уравнения первого порядка
С помощью MS Excel можно численно различными методами находить производные, интегралы, решать нелинейные алгебраические уравнения, обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и т.д. Многие научные и технические задачи приводят к решению дифференциальных уравнений. В большинстве случаев дифференциальные уравнения, которые можно проинтегрировать известными методами, встречаются редко. В связи с этим особое значение имеют приближенные методы решения дифференциальных уравнений. К известным методам относятся метод Эйлера и метод Рунге–Кутта.
3.8.1. Математическая постановка задачи
Дано дифференциальное уравнение первого порядка вида:
удовлетворяющее начальному условию:
.
Необходимо
найти решение дифференциального
уравнения, удовлетворяющее заданному
начальному условию, на отрезке
.
Метод Эйлера для задачи Коши обыкновенного дифференциального уравнения первого порядка заключается в том, что решение уравнения вычисляется по следующей рекуррентной формуле:
,
где
.
В методе Рунге–Кутта 4-го порядка решение задачи Коши обыкновенного дифференциального уравнения первого порядка задается рекуррентной формулой вида:
,
где
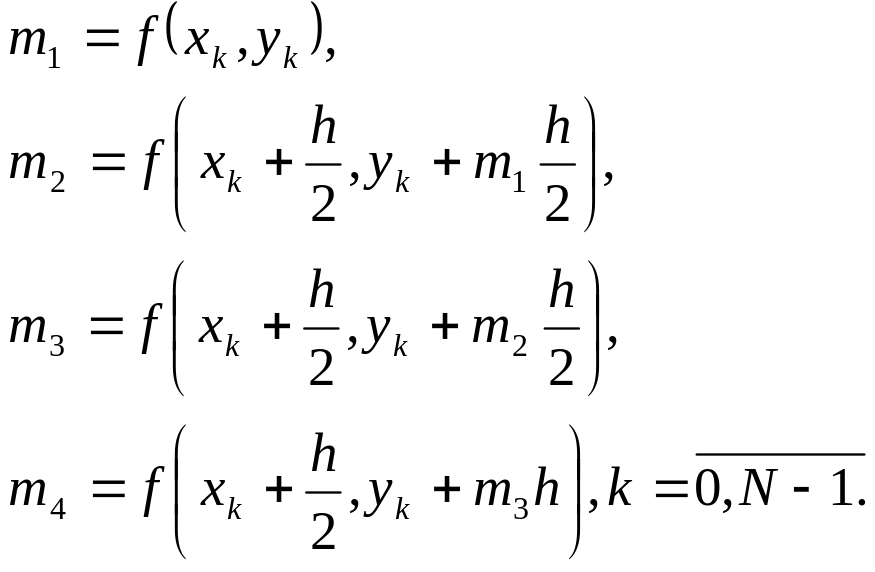
Пример. Найти точное и численное решение дифференциального уравнения:
удовлетворяющее начальному условию:
Провести сравнительный графический анализ решения дифференциального уравнения на отрезке [0,Т], где Т может принимать любые значения, полученные непосредственным интегрированием и с помощью методов Эйлера и Рунге–Кутта.
Решение
Заданное уравнение является линейным неоднородным уравнением первого порядка. Точное решение задачи Коши для этого уравнения имеет вид:
Для получения числовых значений на отрезке [0,T] необходимо подставить в последнее соотношение значения х с шагом h=T/N, где N – число точек на отрезке [0,T].
С помощью пакета MS Excel можно легко реализовать алгоритмы численного решения дифференциального уравнения и построить графики для точного и приближенных решений дифференциального уравнения.
Формулы для вычислений, используемые при решении заданного дифференциального уравнения, представлены в табл. 10 и 11.
Таблица 10
Формулы для вычислений по методу Эйлера
Введенные формулы для вычислений |
Ячейки |
Формула |
Величина шага |
E14 |
=($E$10-$E$8)/$E$12 |
Точное решение уравнения |
F4 |
=EXP(2*H4)-EXP(H4)+H4/2+$F$3 |
Решение уравнения по методу Эйлера |
G4 |
=G3+$E$14*(2*G3+EXP(H4)-H4) |
Значение переменной х |
H4 |
=$H3+$E$14 |
Таблица 11
Формулы для вычислений по методу Рунге-Кутта
Введенные формулы для вычислений |
Ячейки |
Формула |
|
Расчет коэффициентов для метода Рунге–Кутта |
m1 |
I4 |
=2*M3+EXP(H4)-H4 |
m2 |
J4 |
=2*(M3+I4*$E$14/2)+EXP(H4+$E$14/2)-H4-$E$14/2 |
|
m3 |
K4 |
=2*(M3+J4*$E$14/2)+EXP(H4+$E$14/2)-H4-$E$14/2 |
|
m4 |
L4 |
=2*(M3+K4*$E$14/2)+EXP(H4+$E$14/2)-H4-$E$14 |
|
Метод Рунге–Кутта |
M4 |
=M3+(I4+2*J4+2*K4+L4)*$E$14/6 |
|
На рабочих листах решение можно оформить по образцам рис. 1 и 2.
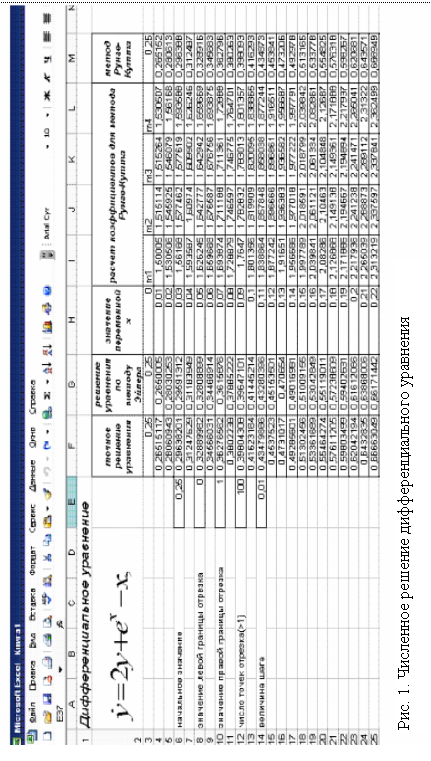
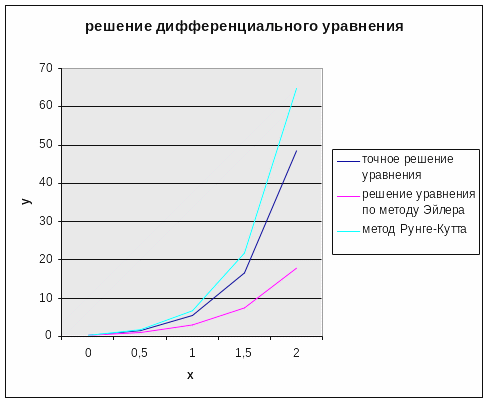
Рис. 2. Графики для точного и приближенного решения дифференциального уравнения