Розрахунково-графічна робота №6

“Визначення переміщень у статично визначеній плоскій рамі”

Завдання: від заданого зовнішнього навантаження для плоскої рами (розрахункові схеми на рис. 6.1) побудувати епюри внутрішніх зусиль М, Q і N,

Варіанти розрахункових схем складних рам

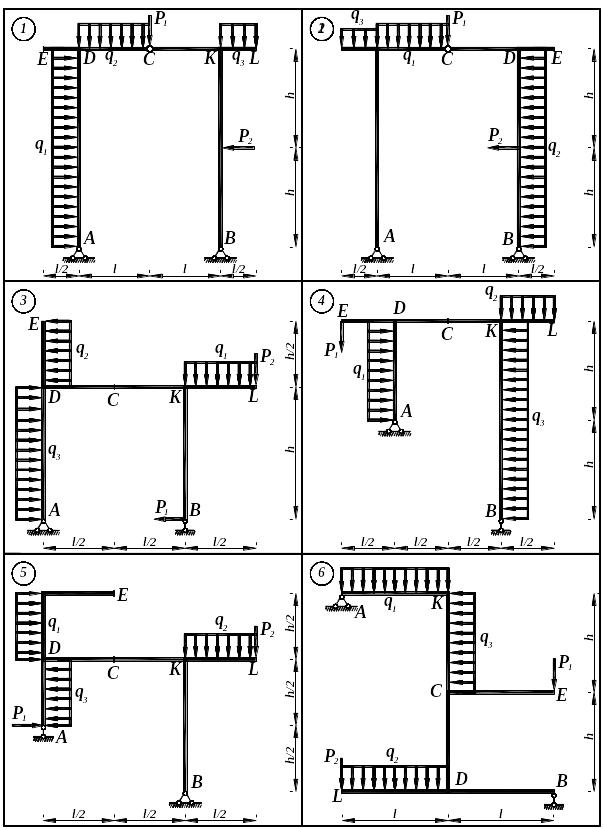
Рис. 6.1.

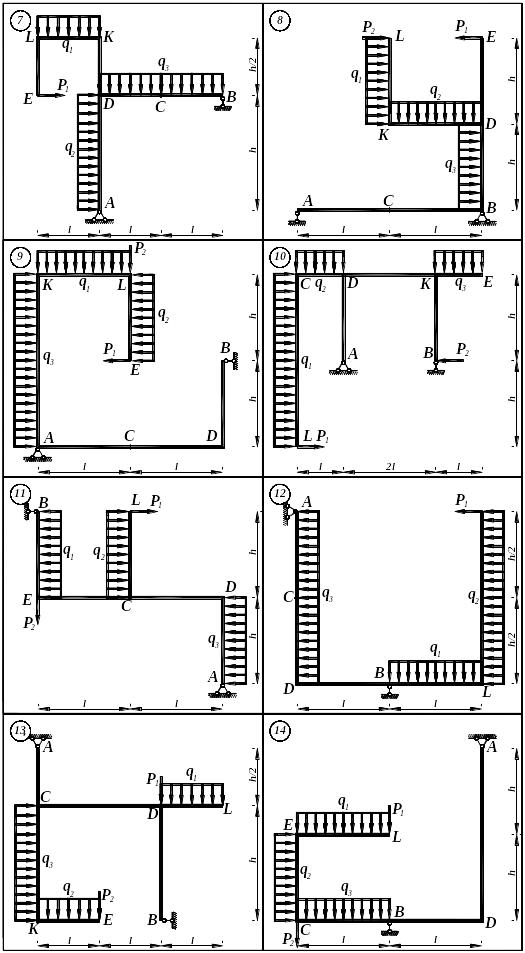
Рис. 6.1. (продовження)

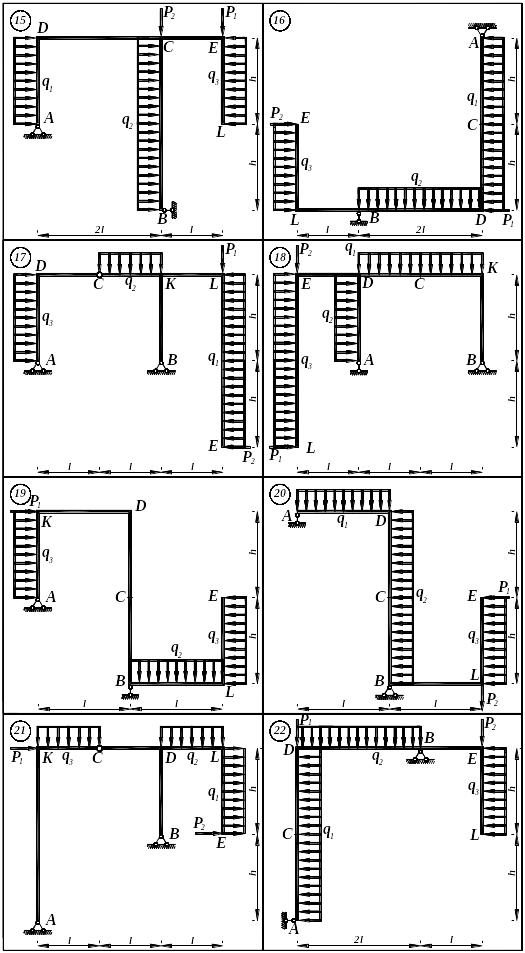
Рис. 6.1. (продовження)

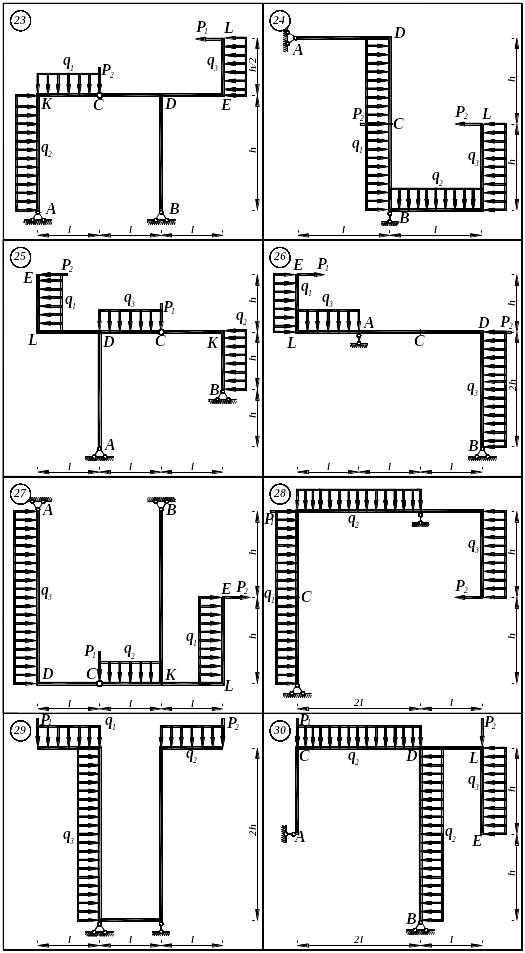
Рис. 6.1. (продовження)

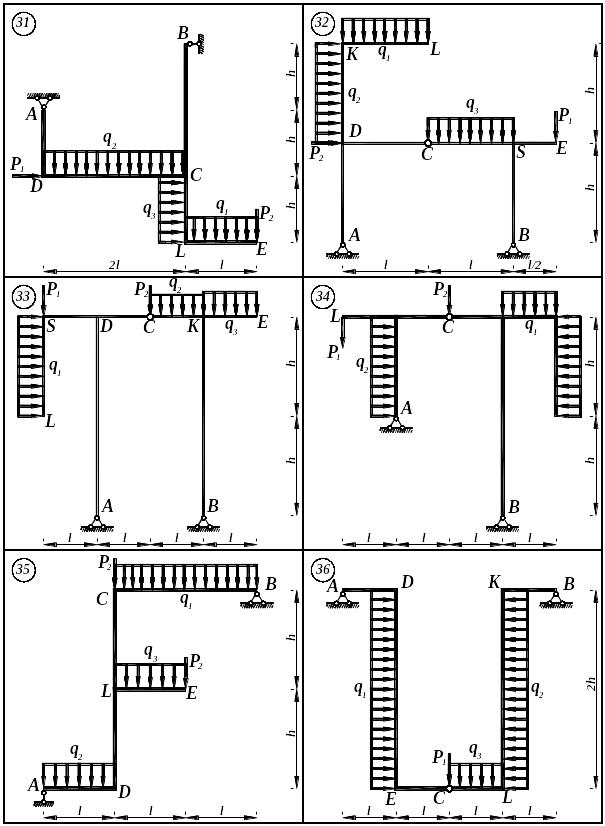
Рис. 6.1. (продовження)

підібрати поперечний переріз ригеля й стояка у вигляді у вигляді двотавра та визначити вказані лінійні та кутові переміщення з урахуванням їх жорсткостей. Перевірити міцність та жорсткість конструкції, якщо МПа, . Числові дані для розрахунку подано в табл. 6.1.

Таблиця 6.1.

Вихідні числові дані до розрахункових схем плоских рам

№ рядка	Розміри, м			Навантаження					Визначити переміщення в перерізі
	l	h		q1, кН/м	q2, кН/м	q3, кН/м	Р1, кН	Р2, кН	гори-зонтальне	верти-кальне	кут повороту
1	2	2	2	–	40	–	80	–	L	E	D
2	2,6	2	1,5	20	–	–	60	–	E	L	A
3	4	2,6	1	–	–	20	–	60	C	E	B
4	2,4	2	1,2	–	20	–	80	–	C	L	D
5	2	2,4	1,4	40	–	–	–	80	L	L	B

Порядок виконання роботи

1. В прийнятому масштабі накреслити відповідну до варіанту схему складної рами (рис. 6.1), вказати на ній всі розміри, нанести зовнішнє навантаження з таблиці 6.1.

2. Побудувати епюри внутрішніх зусиль М, Q і N.

3. Підібрати поперечний переріз рами.

4. Побудувати одиничні епюри .

5. Визначити лінійні та кутове переміщення.

6. Перевірити міцність та жорсткість конструкції.

Приклад розрахунку переміщень у плоскій рамі

Для даної рами (рис. 6.2) побудувати епюри внутрішніх зусиль М, Q і N, підібрати поперечний переріз ригеля й стояка у вигляді двотавра та визначити горизонтальне переміщення точки А ( ), вертикальне переміщення точки В ( ) та кутове переміщення точки С ( ). Відношення жорсткостей ригеля до стояка . Перевірити міцність та жорсткість конструкції, якщо МПа, .

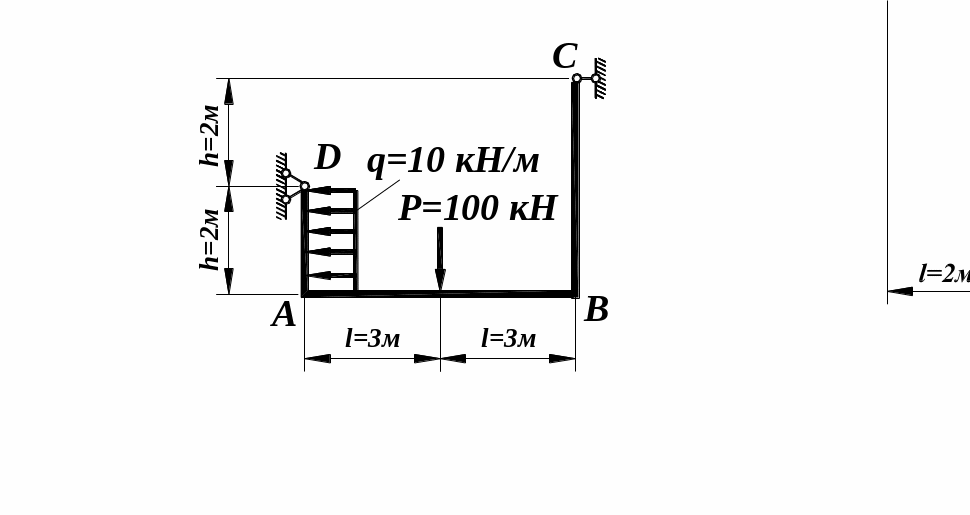
Рис. 6.2.

1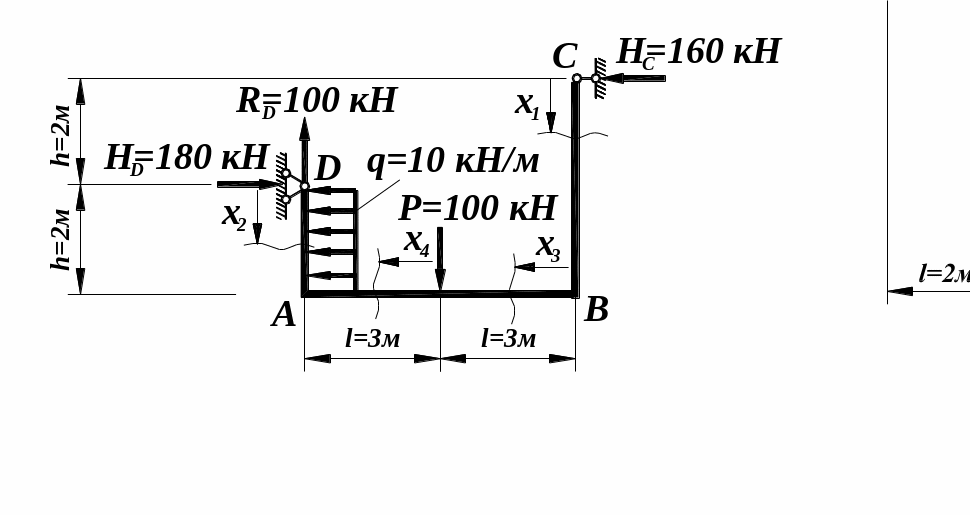 . Визначаємо опорні реакції:

а)  ;

кН;

б)  ; кН;

в)  ;

кН.

2. Будуємо епюри М, Q і N по ділянках:

; кНм; кНм.

кН.

кН.

; кНм; кНм; кНм.	; кН; кН.
	кН.

кНм.

кН.

кН.

; кНм; кНм.

кН.

кН.

Показуємо отримані значення зусиль на епюрах М, Q і N:

3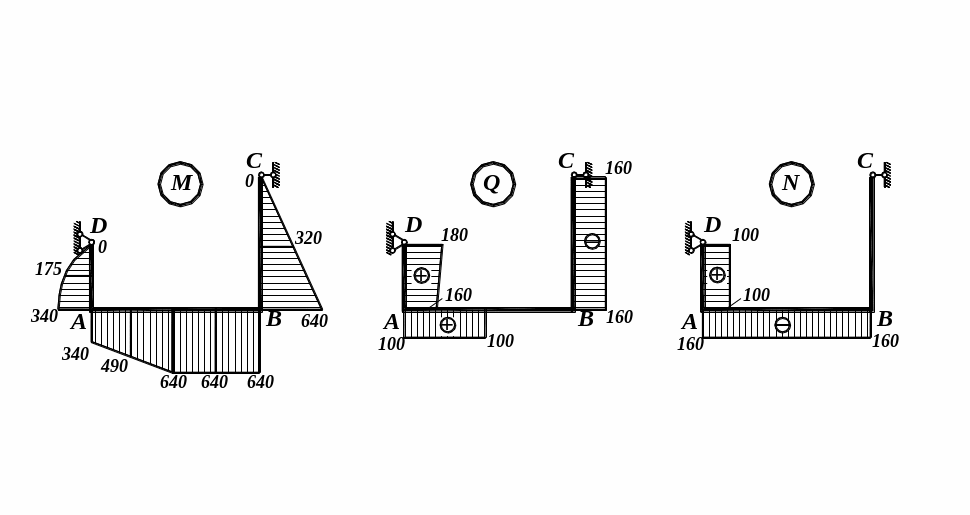 . Підбираємо двотавровий поперечний переріз рами. Умова міцності:

МПа.

Відкинувши перший доданок з умови міцності визначаємо орієнтовний момент опору:

м³ см³.

За сортаментом підбираємо двотавровий переріз, для якого момент опору і площа поперечного перерізу задовольнятимуть умову міцності. Оскільки одного двотавра недостатньо, то підбираємо переріз із двох елементів.

Для одного двотавра №60: см², см³, см⁴, а для двох елементів: см², см³, см⁴.

4. Розглядаємо одиничні стани для визначення переміщень і будуємо одиничні епюри моментів .

4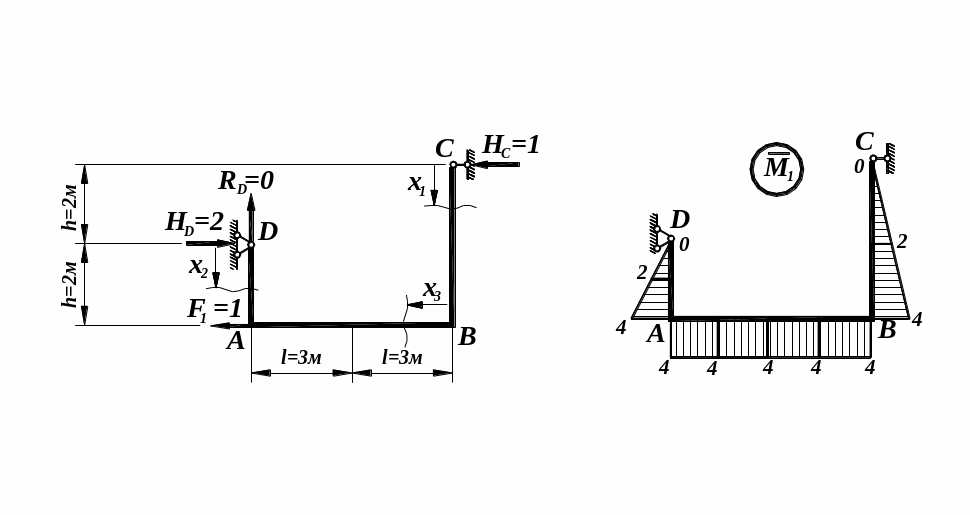 .1. Для визначення горизонтального переміщення точки А ( ) до даної рами необхідно в точці А по напрямку її ймовірного переміщення прикласти горизонтальну одиничну силу та від її дії визначити опорні реакції і побудувати одиничну епюру моментів .

Визначаємо опорні реакції:

а)  ;  ;

б)  ;

в)  ;  .

Записуємо рівняння моментів по ділянках:

; м; м.

; м; м.

м.

Показуємо отримані значення зусиль на епюрі .

4.2. Для визначення вертикального переміщення точки В ( ) до даної рами необхідно в точці В по напрямку її ймовірного переміщення прикласти вертикальну одиничну силу та від її дії визначити опорні реакції і побудувати одиничну епюру моментів .

В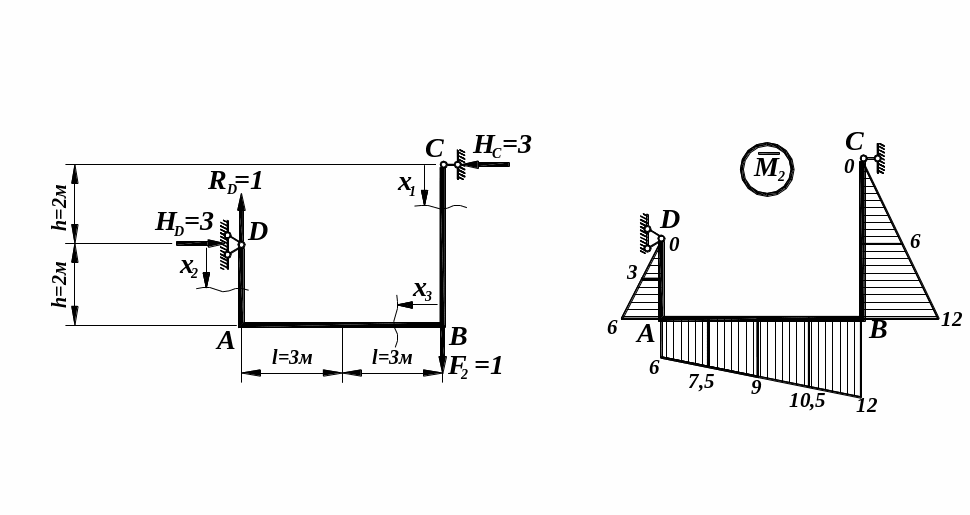 изначаємо опорні реакції:

а)  ;  ;

б)  ;  ;

в)  ;  .

Записуємо рівняння моментів по ділянках:

; м; м.

; м; м.

;

м; м.

Показуємо отримані значення зусиль на епюрі .

4.3. Для визначення кута повороту точки С до даної рами необхідно в точці С по напрямку її ймовірного кута повороту прикласти одиничний момент та від його дії визначити опорні реакції і побудувати одиничну епюру моментів .

В изначаємо опорні реакції:

а)  ;  м ^–1;

б)  ; в)  ;  м ^–1.

Записуємо рівняння моментів по ділянках:

; ; .

; ; .

.

Показуємо отримані значення зусиль на епюрі .

5. Визначаємо переміщення , та з урахуванням відношення моментів інерції ригеля до стояка за загальною формулою інтегралу Мора:

.

Даний інтеграл можна обчислити за способом Сімпсона-Корноухова:

,

де – довжина ділянки, на якій перемножуються епюри та ;

– модуль пружності матеріалу рами;

– момент інерції поперечного перерізу вказаної ділянки;

– відповідно початкове, середнє та кінцеве значення ;

– відповідно початкове, середнє та кінцеве значення .

5.1. Для визначення переміщення необхідно перемножити епюри моментів та :

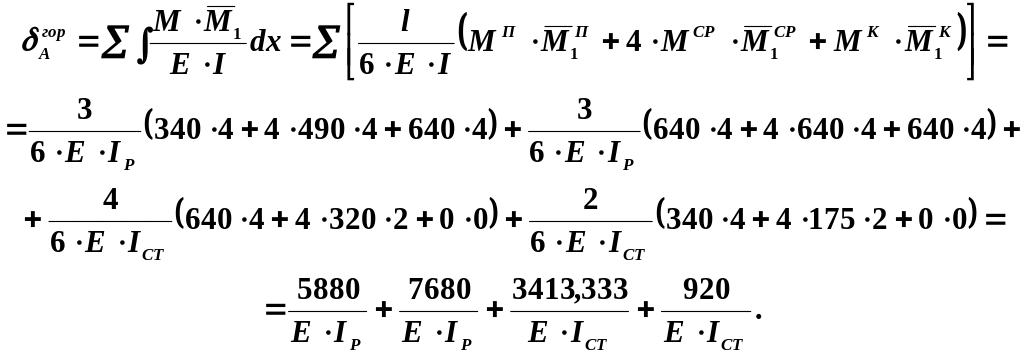
Необхідно звернути увагу на те, що при перемноженні ординат епюр на горизонтальних ділянках (ригелях) в знаменник підставляється момент інерції , а на вертикальних ділянках (стійках) – момент інерції .

З урахуванням відношення можна в знаменнику переміщення виконати заміну – і результат звести до одного знаменника :

.

5.2. Для визначення переміщення необхідно перемножити епюри моментів та :

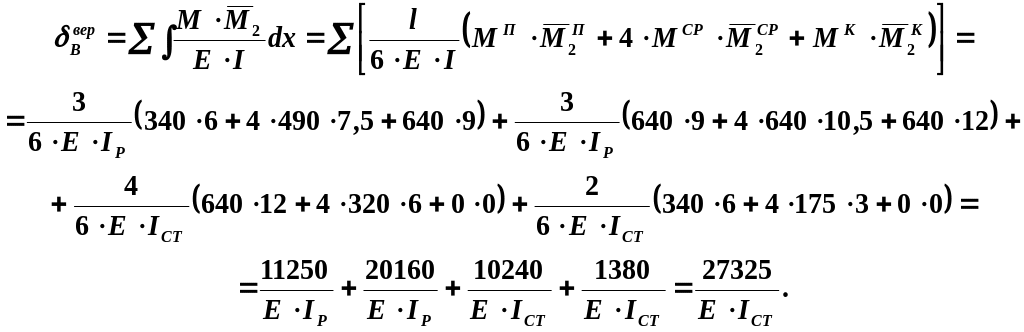5.3. Для визначення кута повороту перемножуємо епюри та :

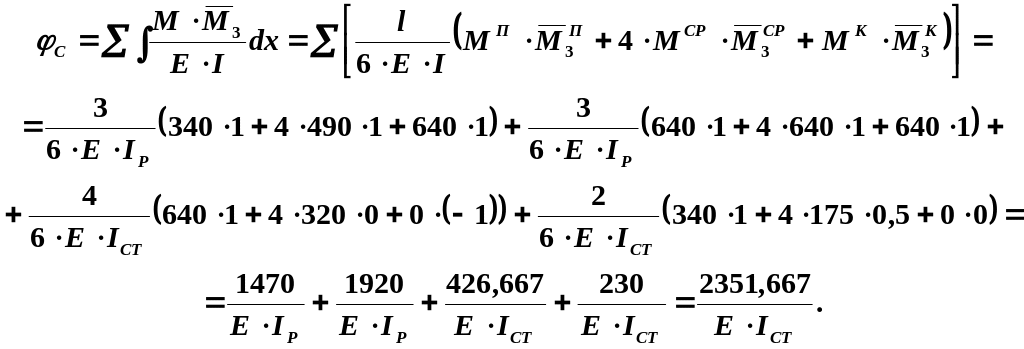
6. Перевіряємо міцність та жорсткість конструкції рами, якщо МПа, м = см. Умова міцності рами:

МПа.

МПа МПа.

Умова міцності виконується!

Для визначення числових значень переміщень необхідно в знаменник підставити відповідні значення модуля пружності для сталі ( МПа), а також моменту інерції поперечного перерізу рами з двох двотаврів №55 ( см⁴). Умова жорсткості рами: см.

м = см см.

м = см см.

рад = ^о.

Умови жорсткості не виконуються! Для їх виконання необхідно підібрати інший поперечний переріз рами.

75