1.3.2. Теорема (критерий Коши существования предела

функции)

Для того, чтобы существовал конечный предел , необходимо и достаточно, чтобы функция была определена в окрестности точки а, за исключением, быть может, самой точки а, и для любого >0 существовала такая окрестность , что, каковы бы ни были точки , , , , выполняется неравенство

1.3.3. Непрерывность функции в точке

После введения понятия предела функции легко определить непрерывную функцию.

Определение.

Функция , определенная в некоторой окрестности , называется непрерывной в этой точке, если

.

Рассмотрим 3 графика:

( 1)

( 2)

(3)

Графики отличаются только значением . В первом случае функция вообще не определена в точке , поэтому говорить о непрерывности не приходится. Во втором случае функция определена при , но – функция не является непрерывной. И только в третьем случае и функция непрерывна.

Замечание.

Если в первом случае доопределить таким образом, что , то функция становится непрерывной. Т.е. случай (1) совпадает с (3). Если же такого доопределения нет, то эти случаи различны.

Согласно определению предела функции в точке это определение эквивалентно следующему.

Определение.

Функция называется непрерывной в точке , если она определена в некоторой окрестности точки и для

любого >0 существует такое , что для всех x, для которых , имеет место неравенство

Это определение (на языке ) позволяет дать следующую наглядную геометрическую интерпретацию для непрерывной функции. Рассмотрим график функции , непрерывной в точке x = .

Так как из неравенства следует неравенство , то это значит, что для всех точек x, отстоящих от не далее, чем на , точка М графика непрерывной функции лежит внутри полосы шириной (заштрихована), ограниченной прямыми и . Мы можем потребовать, чтобы ширина этой полосы была как угодно малой; для непрерывной функции всегда найдется соответствующее , определяющее – окрестность точки x = .

Можно дать определение и на языке последовательностей.

Определение.

Функция называется непрерывной в точке , если она определена в некоторой окрестности точки и для любой последовательности .

1.3.4. Односторонние пределы

Определение.

Число b называется правым (левым) пределом функции в точке x = a, если для любой сходящейся к а последовательности значений аргумента x, элементы x_n которой больше (меньше) а, соответствующая последовательность

сходится к b.

Записывают так: или .

Для левого предела:

или .

С учетом введенных определений ясно, что функция непрерывна в точке , если:

,

т.е. левый предел должен равняться правому и равняться значению функции в точке .

Пример: когда левый и правый пределы не совпадают

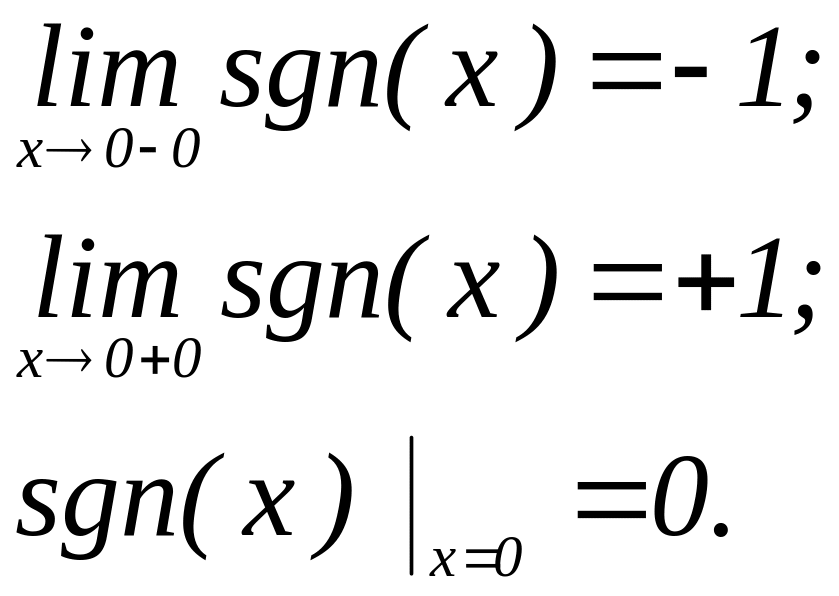
Функция не является непрерывной в точке .

Вернемся к самому первому определению. Функция непрерывна, если . Тогда ; или .

Обозначим , . Тогда , – приращение аргумента, – приращение функции, соответствующее приращению .

Таким образом, функция непрерывна в точке , если приращение функции стремится к нулю при любом способе стремления к нулю приращения аргумента .

x

может быть любого

знака.

Отметим важное свойство непрерывных функций.

Пусть функция непрерывна в точке . Выберем последовательность , так чтобы . Тогда . Таким образом, для непрерывной функции можно поменять местами операции предела lim и взятие функции. На языке математики говорят, что для непрерывной функции операторы lim и f коммутативны (перестановочны). Пример: можно доказать, что функция непрерывна в любой точке. Поэтому .