
- •Предисловие
- •1. Введение в анализ
- •1.1. Основные элементарные функции
- •1.1.1. Некоторые множества вещественных чисел
- •1.1.4. Понятие о функции
- •1.2. Предел последовательности. Бесконечно малые и
- •1.2.1. Предел поcледовательности
- •1.2.2. Ограниченные и неограниченные последователь-
- •1.2.3. Бесконечно малые и бесконечно большие последо-
- •1.2.5. Основные теоремы о пределах
- •1.2.6. Монотонные последовательности
- •1.2.7. Понятие о подпоследовательности числовой по-
- •1.2.8. Необходимое и достаточное условие сходимости
- •1.3. Функция. Предел функции. Непрерывность функции
- •1.3.1. Определение предела функции
- •1.3.2. Теорема (критерий Коши существования предела
- •1.3.3. Непрерывность функции в точке
- •1.3.4. Односторонние пределы
- •1.3.5. Свойства функций, непрерывных в точке
- •1.3.6. Два замечательных предела
- •1.3.7. Эквивалентные бесконечно малые функции и их
- •1.3.8. Монотонные функции. Теорема о существовании
- •1.3.9. Разрывы первого и второго рода
- •2.2. Основные правила и формулы дифференцирования
- •2.3. Дифференциал функции
- •2.4. Производная сложной функции, обратной функции, функции, заданной параметрически
- •Производная обратной функции
- •Производные обратных тригонометрических функций
- •Аналогично
- •2.5 Уравнения касательной и нормали к графику функ-
- •Рассмотрим кривую, уравнение которой .
- •2.6. Производные высшего порядка. Формула Лейбница
- •2.7. Возрастание и убывание функции в окрестности
- •Доказательство:
- •2.8. Поведение функции на отрезке. Теоремы о среднем
- •2.9. Критерии возрастания и убывания функции на ин-
- •2.10. Формула Тейлора Начнем с того, что выведем формулу Тейлора для многочлена
- •Формулы Тейлора для важнейших элементарных функций
- •2.11. Раскрытие неопределенностей. Правило Лопиталя
- •Замечание 1.
- •2.12. Исследование функции одной переменной
- •2.12.1. Отыскание участков монотонности функции
- •2.12.2. Отыскание точек возможного экстремума
- •2.12.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.12.4. Асимптоты графика функции
- •2.12.5. Общая схема исследования функции и построения ее графика
- •Целесообразно провести следующие исследования:
- •2.13. Наибольшее и наименьшее значение функции, непрерывной на отрезке
- •3. Функции нескольких переменных
- •3.1. Примеры функций нескольких переменных
- •3.2. Определение функции двух переменных. Область определения функции двух переменных
- •3.3. Геометрическое изображение функции двух переменных
- •3.4. Предел и непрерывность функции двух переменных
- •3.5. Частные приращения и частные производные
- •3.6. Полное приращение и полный дифференциал. Использование дифференциала для приближенных вычислений
- •3.7. Сложная функция и ее полная производная
- •3.8. Производная неявно заданной функции
- •3.9. Частные производные высших порядков
- •3.10. Производная по направлению
- •Где и стремятся к нулю, если . Разделим все члены в (3.10.1) на :
- •То , тогда и
- •Аналогично производные и являются производными вдоль положительных направлений координатных осей и .
- •3.11. Градиент
- •3.12. Формула Тейлора для функции двух переменных
- •3.13. Экстремум функции двух переменных
- •3.14. Условный экстремум функции многих переменных
- •Логинов Вениамин Анатольевич
- •Дифференциальное исчисление
- •Курс лекций по дисциплине «Математика» для студентов
- •Инженерных и экономических специальностей мгавт
- •117105, Г. Москва, Новоданиловская нанбережая, строение 2, корп. 1
УДК 514
ББК 22.143
Логинов В.А. Дифференциальное исчисление. – М. Альтаир, 2007. – 154с.
Курс лекций по дифференциальному исчислению подготовлен доцентом кафедры высшей математики Московской государственной академии водного транспорта, кандидатом технических наук В.А. Логиновым.
Курс лекций предназначен для студентов МГАВТ и полностью соответствует учебным программам по дисциплине «Математика» для технических и экономических специальностей.
Изложены теория пределов последовательностей и функций, основы дифференциального исчисления функции одной переменной, приложения производной к исследованию функций и построению их графиков. Даны основы дифференциального исчисления функций многих переменных.
Рассмотрено на заседании кафедры высшей математики
Протокол № от 2006 г.
Рекомендовано к изданию на Учебно-методическом совете МГАВТ
Протокол № от 2006 г.
Рецензент доцент Бакулин С.А.
УДК 514
ББК 22.143
© Логинов В.А., 2007.
© МГАВТ, 2007.
Содержание
ПРЕДИСЛОВИЕ...........................................................................6
ПРЕДИСЛОВИЕ 5
1. ВВЕДЕНИЕ В АНАЛИЗ 6
1.1. Основные элементарные функции 6
1.1.1. Некоторые множества вещественных чисел 6
1.1.2. Основные операции над множествами 7
1.1.3. Множества вещественных чисел, ограниченные 7
1.1.4. Понятие о функции 8
1.2. Предел последовательности. Бесконечно малые и 18
1.2.1. Предел поcледовательности 18
1.2.2. Ограниченные и неограниченные последователь- 22
1.2.3. Бесконечно малые и бесконечно большие последо- 24
1.2.4. Теоремы о бесконечно малых последовательно- 25
1.2.5. Основные теоремы о пределах 28
1.2.6. Монотонные последовательности 33
1.2.7. Понятие о подпоследовательности числовой по- 37
1.2.8. Необходимое и достаточное условие сходимости 38
1.3. Функция. Предел функции. Непрерывность 39
функции 39
1.3.1. Определение предела функции 39
1.3.2. Теорема (критерий Коши существования предела 42
1.3.3. Непрерывность функции в точке 42
1.3.4. Односторонние пределы 45
1.3.5. Свойства функций, непрерывных в точке 46
1.3.6. Два замечательных предела 49
1.3.7. Эквивалентные бесконечно малые функции и их 53
1.3.8. Монотонные функции. Теорема о существовании 54
1.3.9. Разрывы первого и второго рода 56
1.3.10. Функции, непрерывные на отрезке 58
2.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 59
2.1. Производная. Ее физический и геометрический 59
2.2. Основные правила и формулы дифференцирования 63
2.3. Дифференциал функции 65
2.4. Производная сложной функции, обратной функции, 66
функции, заданной параметрически 66
2.5 Уравнения касательной и нормали к графику функ- 70
2.6. Производные высшего порядка. Формула Лейбница 70
2.7. Возрастание и убывание функции в окрестности 74
2.8. Поведение функции на отрезке. Теоремы о среднем 75
2.9. Критерии возрастания и убывания функции на ин- 78
2.10. Формула Тейлора 79
2.11. Раскрытие неопределенностей. Правило Лопиталя 84
2.12. Исследование функции одной переменной 87
2.12.1. Отыскание участков монотонности функции 87
2.12.2. Отыскание точек возможного экстремума 88
2.12.3. Выпуклость и вогнутость кривой. Точки 91
перегиба 91
2.12.4. Асимптоты графика функции 96
2.12.5. Общая схема исследования функции и 98
построения ее графика 98
Для качественного исследования графика функции y=f(x) 98
целесообразно провести следующие исследования: 98
2.13. Наибольшее и наименьшее значение функции, 102
непрерывной на отрезке 102
3.12. Формула Тейлора для функции двух переменных 124
Логинов Вениамин Анатольевич 136
Предисловие
Настоящий курс лекций соответствует утвержденным рабочим программам по дисциплине «Математика» для студентов МГАВТ инженерных и экономических специальностей.
В лекциях отражены разделы высшей математики, изучаемые студентами во II семестре: теория пределов последовательностей и функций, основы дифференциального исчисления функции одной переменной, приложения производной к исследованию функций и посроению их графиков, основы дифференциального исчисления функций многих переменных.
В качестве задачника для практических занятий автор рекомендует «Задачи и упражнения по математическому анализу для втузов» под редакцией Б.П. Демидовича, а также задачник П.Е. Данко, А.Г. Попова и Т.Я. Кожевниковой «Высшая математика в упражнениях и задачах», часть I.
1. Введение в анализ
1.1. Основные элементарные функции
1.1.1. Некоторые множества вещественных чисел
В
математике множество относится к так
называемым первичным, неопределяемым
понятиям (в школьной математике такими
первичными понятиями являются понятия
числа, точки, прямой и т.д.). Под множеством
понимается собрание или совокупность
каких-либо предметов. Примеры: множество
деревьев на поляне; множество всех целых
чисел. Обозначаются множества обычно
большими латинскими буквами: A,
B,U
и т.д. Если x
– один из предметов множества A,
то записывают так:
![]() (x
принадлежит A).
Если какой-то элемент не принадлежит
множеству A,
то пишут так:
(x
принадлежит A).
Если какой-то элемент не принадлежит
множеству A,
то пишут так:
![]() .
.
В дальнейшем мы будем иметь дело с различными множествами действительных чисел. Наиболее часто используются следующие числовые множества, задаваемые с помощью неравенств:
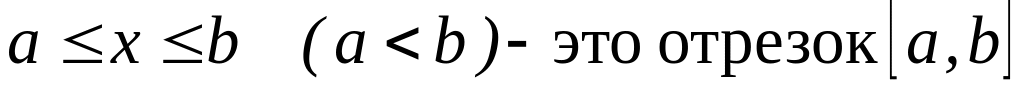 ;
a
и b
– граничные точки отрезка; любое число
a<x<b
– это внутренняя точка отрезка;
;
a
и b
– граничные точки отрезка; любое число
a<x<b
– это внутренняя точка отрезка;a<x<b , (a,b) – интервал;
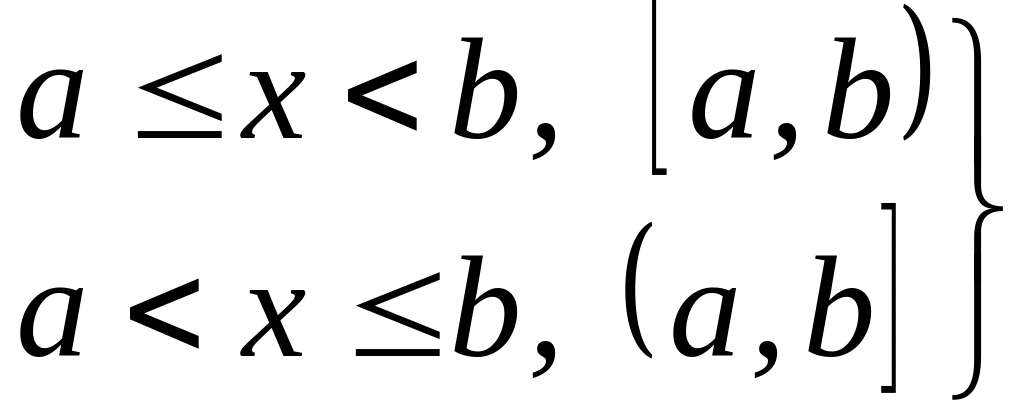 –
полуинтервалы;
–
полуинтервалы;Любой интервал, содержащий точку C, называют ее
окрестностью;
Интервал
 называется
называется
 -окрест-ностью
точки C;
-окрест-ностью
точки C;Множество всех вещественных чисел будем называть бесконечной числовой прямой, обозначение:
 ;
; –
полупрямые;
–
полупрямые;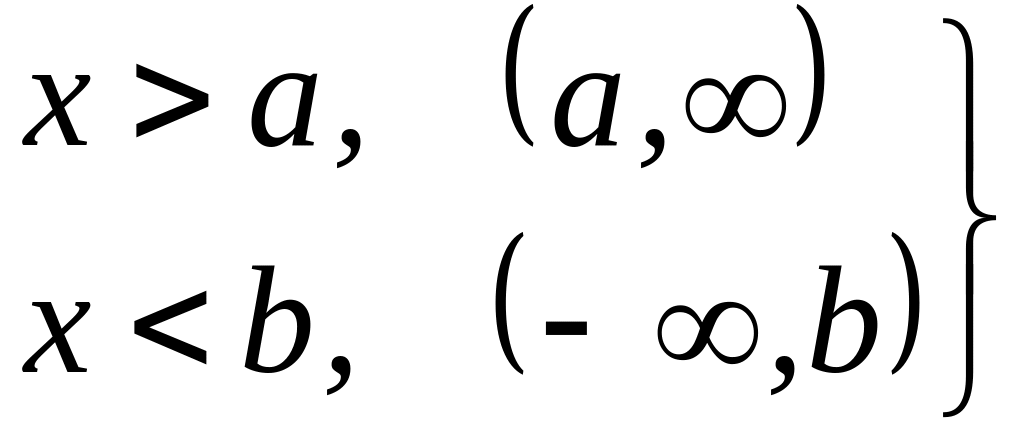 –
открытые
полупрямые.
–
открытые
полупрямые.
1.1.2. Основные операции над множествами
Объединением множеств A и B называется множество
 .
.Пересечением множеств A и B называется множество
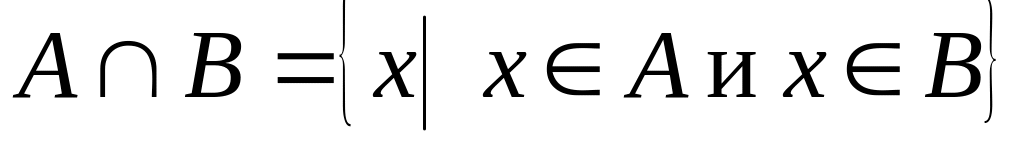 .
.Разностью множеств A и B называется множество
 .
.
Запись
![]() означает, что каждый элемент множества
A
является элементом множества B.
означает, что каждый элемент множества
A
является элементом множества B.
Множества
A
и B
называются равными, если
![]() (состоят из одних и тех же элементов).
(состоят из одних и тех же элементов).
1.1.3. Множества вещественных чисел, ограниченные
сверху или снизу
Рассмотрим
произвольное множество
![]() вещественных чисел, содержащее хотя бы
одно число. Отдельные числа этого
множества будем называть его элементами.
вещественных чисел, содержащее хотя бы
одно число. Отдельные числа этого
множества будем называть его элементами.
Определение.
Множество
вещественных чисел
называется ограниченным сверху (снизу),
если существует такое вещественное
число M
(число m),
что каждый элемент x
множества
удовлетворяет неравенству
![]()
При
этом число M
(число m)
называется верхней гранью (нижней
гранью) множества
.
Любое ограниченное сверху множество
имеет бесконечно много верхних граней.
Любое
![]() ,
так же, как и M,
является верхней гранью. Аналогичное
замечание можно сделать относительно
нижней грани.
,
так же, как и M,
является верхней гранью. Аналогичное
замечание можно сделать относительно
нижней грани.
Естественно, возникают вопросы: имеется ли среди верхних граней множества наименьшая? Или имеется ли среди нижних граней наибольшая?
Определение.
Наименьшая
из всех верхних граней ограниченного
сверху множества
называется точной верхней гранью этого
множества и обозначается символом
![]() – супремум. Наибольшая из всех нижних
граней ограниченного снизу множества
называется точной нижней гранью этого
множества и обозначается
– супремум. Наибольшая из всех нижних
граней ограниченного снизу множества
называется точной нижней гранью этого
множества и обозначается
![]() –
инфинум.
–
инфинум.
Это определение можно сформулировать по другому.
Число
![]() называется точной верхней (точной
нижней) гранью множества
,
если выполнены следующие два требования:
называется точной верхней (точной
нижней) гранью множества
,
если выполнены следующие два требования:
Каждый элемент множества удовлетворяет неравенству

Каково бы ни было вещественное число
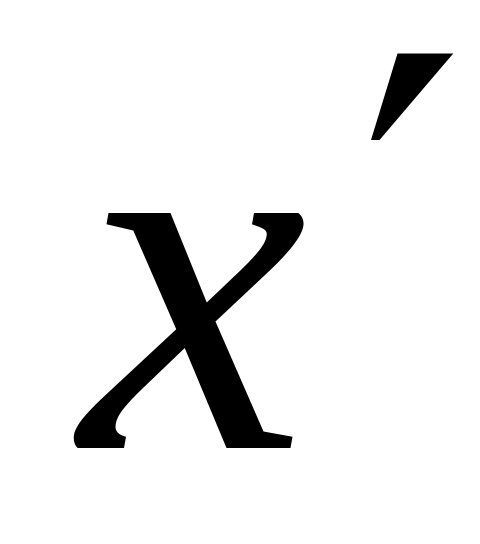 ,
меньшее
,
меньшее
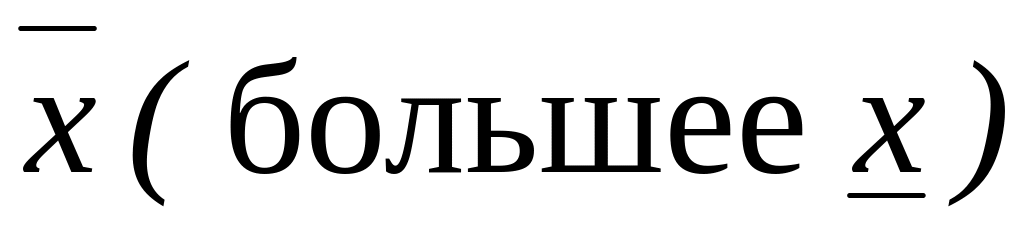 ,
найдется хотя бы один элемент x
множества
,
удовлетворяющий неравенству
,
найдется хотя бы один элемент x
множества
,
удовлетворяющий неравенству
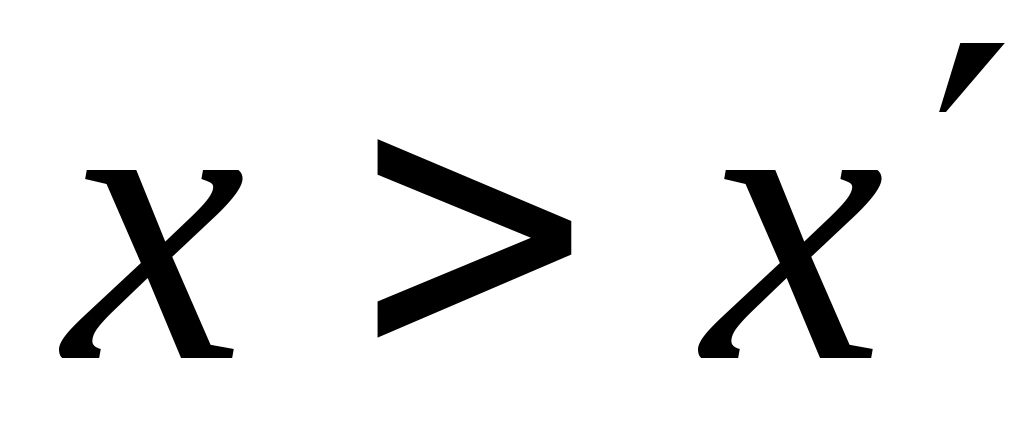 (
( ).
).
Теорема.
Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху (снизу), то существует вещественное число , являющееся точной верхней (точной нижней) гранью этого множества.
Формулировка этой теоремы дается без доказательства.
