32. Формула Ито для согласования случайных последовательностей (теорема 58). Формула Ито для произведения двух семимартингалов. Квадратическая и взаимная вариация (определения).

Теорема 58 (формула Ито). Пусть и множество ограниченных непрерывно дифференцируемых функций . Пусть семимартингал относительно меры Р. Тогда Р - п. н. справедливо равенство

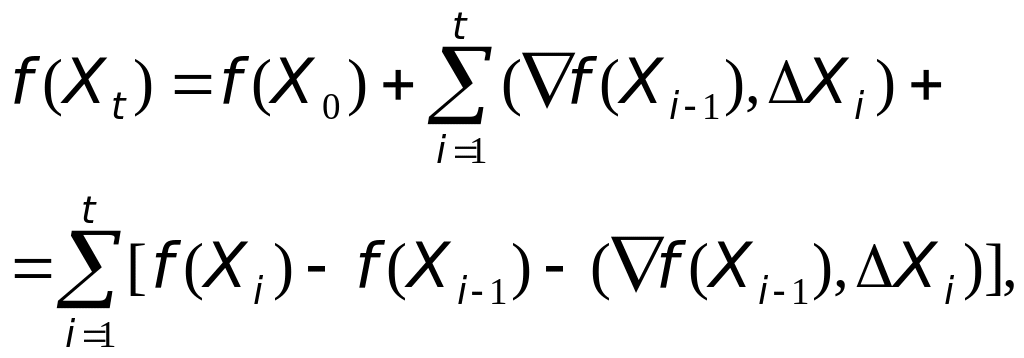(16)

где 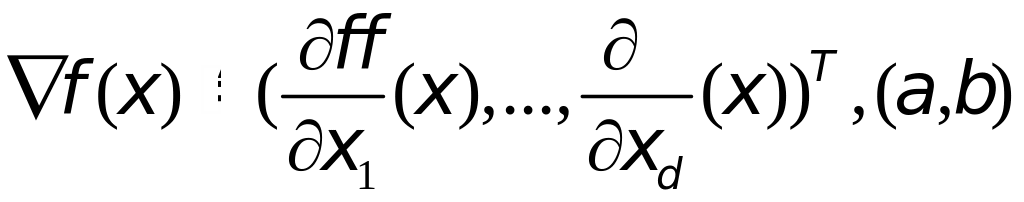- скалярное произведение в .

Доказательство. Очевидно равенство 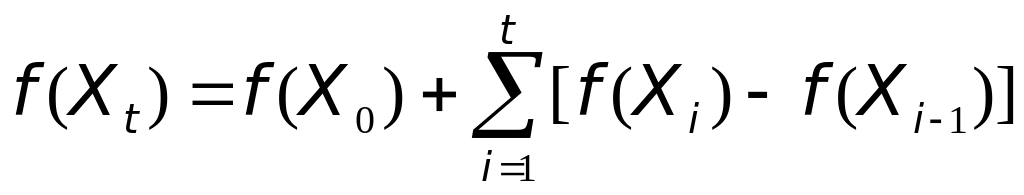Р - п. н. Отсюда следует (16). Доказательство закончено.

Их формулы Ито (16) легко получить представление для произведения семимартингалов.

Теорема 59. Пусть и семимартингалы со значениями относительно меры P. Тогда P – п.н. справедливо равенство

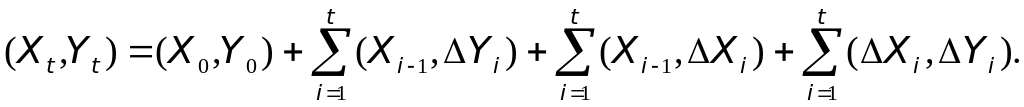
В частности

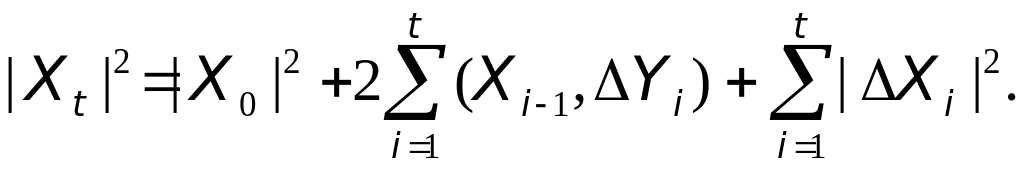
Определение. Квадратической вариацией семимартингала , обозначаемого через , назовем случайную последовательность определяемую равенством

Определение. Взаимной вариацией семимартингалов и , обозначаемую через назовем случайную последовательность такую, что .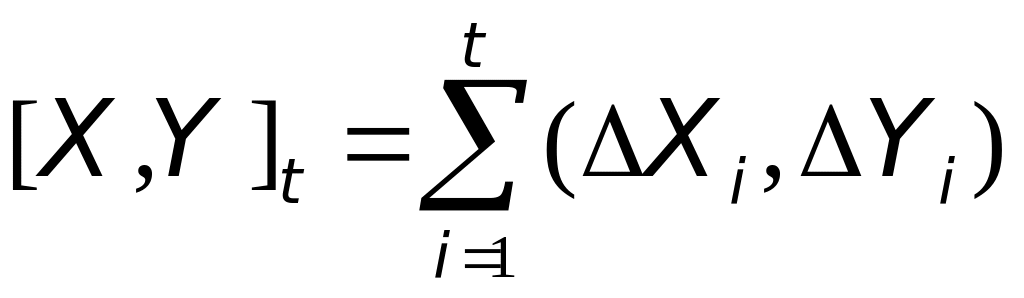

33. Определения квадратично интегрируемого мартингала и его характеристики. Характеризация характеристики квадратично интегрируемого мартингала (теорема 60).

Определение. Пусть мартингал относительно меры Р и , тогда такой мартингал называется квадратично интегрируемым.

Определение. Предсказуемая возрастающая последовательность, обозначаемая , называется характеристикой квадратично интегрируемого мартингала , если - мартингал относительно меры Р.

Теорема 60. Если квадратично интегрируемый мартингал, то у него существует единственная характеристика , причем:

i) Р - п. н.,

ii) - мартингал относительно меры Р.

Доказательство. Существование и единственность характеристики квадратично интегрируемого мартингала следует из теоремы Дуба-Мейера. Поэтому Р - п. н. справедливо представление

,

где мартингал относительно меры Р. Отсюда следует, что Р - п. н.

. (17)

Возьмем условное математическое ожидание относительно левой и правой частей (17), имеем Р - п. н.

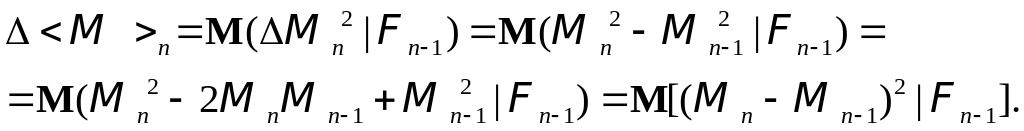
Покажем, теперь, что - мартингал.

Для этого достаточно показать, что Р - п. н.

Действительно, так как

a то . Доказательство закончено.

34. Взаимная характеристика. Ортогональные квадратично интегрируемые мартингалы. Критерий ортогональности (теорема 62).

Определение. Пусть и – квадратично интегрируемые мартингалы, предсказуемый случайный процесс, обозначаемый через , называется взаимной характеристикой квадратичноинтегрируемых мартингалов и , если является мартингалом относительно фильтрации и меры Р.

Теорема 61. Если и квадратично интегрируемые мартингалы, то взаимная характеристика существует и единственна, причем:

i)

ii) Р - п. н.

Доказательство. Сначала заметим, что и – квадратично интегрируемые мартингалы. Поэтому и - являются мартингалами, причем и - единственные предсказуемые возрастающие процессы. Заметим, что и поэтому является мартингалом относительно фильтрации и меры Р.

Отсюда следует утверждение теоремы.

Определение. Пусть , квадратично интегрируемые мартингалы относительно фильтрации и меры Р. Будем говорить, что и ортогональны, если является мартингалом.

Теорема 62. Для того чтобы квадратично интегрируемые мартингалы и были ортогональны, необходимо и достаточно, чтобы Р - п. н. для любого .

Доказательство. Пусть и ортогональны. В силу формулы Ито, имеем

(18)

Заметим, что второе, третье и четвертое слагаемые правой части (18) являются мартингалами, поэтому является мартингалом тогда и только тогда, когда Р - п. н..