14. Сходимость в пространстве Lp, p принадлежит [1, ∞]. Критерий Коши(теорема 24).

Определение. Множество действительных случайных величин таких, что при и , при обозначим через и в этом случае будем писать , . Отметим, что при является банаховым пространством относительно нормы: , при , , при .

Из этих определений следует, что : а) , если ; б) - является гильбертовым пространством относительно скалярного произведения , где .

Определение. Пусть - последовательность случайных величин такая, что . Будем говорить, что сходится в среднем порядка р к случайной величине , если и использовать обозначение .

В частности, если: 1) р=1 и , то говорят, что сходится к в среднем; 2) р=2 и , то говорят, что сходится к в среднеквадратическом смысле и обозначают ; 3) при р = сходимость называется существенно равномерной.

Теорема 24. Пусть последовательность из , . Следующие утверждения эквивалентны:

1) - сходящаяся в последовательность,

2) при .

15. Слабая компактность в L₁. Критерий Данфорда-Петтиса (теорема 26).

Опишем теперь слабую сходимость в .

Определение. Последовательность с называется слабо сходящейся в к случайной величине с , если для любой ограниченной случайной величины справедливо равенство .

Определение. Последовательность случайных величин называется слабо компактной в , если она содержит слабо сходящуюся подпоследовательность.

Приведем критерий слабой компактности Данфорда-Петтиса.

Теорема 26. Для того чтобы последовательность случайных величин с была слабо компактной в необходимо и достаточно, чтобы она была равномерно интегрируема.

16. Относительная слабая компактность семейства вероятностных мер. Теорема Прохорова (теорема 29)

Пусть на (Ω,F,P) задана последовательность случайных элементов со значениями в , где E - польское пространство, т.е. полное сепарабельное метрическое пространство, а алгебра на E.

Определение. Будем говорить, что - последовательность случайных элементов со значениями в E сходится по распределению при к случайному элементу со значениями в E и обозначать , если для любой функции С_b(E), где С_b(E) - пространство непрерывных ограниченных на E функций со значениями в R¹, справедливо ( ) = M ( ).

Определение. Семейство вероятностных мер на называется слабо сходящимся к некоторой мере P₀ и обозначается P_n P₀ , если для любой С_b(E)

= .

Из этих определений вытекает утверждение.

Теорема 27. Пусть - семейство случайных элементов, а соответствующее им семейство распределений , тогда и только тогда, когда P_n P_о , т.е. ( ) = M ( ), для С_b(E).

Определение. Семейство вероятностных мер {P_n}_n>1 на называется относительно компактным, если оно содержит подпоследовательность, слабо сходящуюся к некоторой вероятностной мере Р.

Определение. Семейство вероятностных мер {P_n}_n>1 называется плотным, если для любого >0 существует компакт E такой, что Р_n( < .

Приведем достаточное условие плотности семейства {P_n}_n>1.

Предложение 28. Если последовательность случайных величин , где >0, равномерно интегрируема, то семейство {P_n}_n>1 плотно.

Следующее утверждение играет фундаментальную роль в теории слабой сходимости.

Теорема 29 (Прохоров) Пусть {P_n}_n>1 – семейство вероятностных мер на . {P_n}_n>1 – относительно компактно тогда и только тогда, когда оно является плотным. (без доказательства).

1 7. Неравенства Чебышёва, Йенсена, Гёльдера.

18. Абсолютная непрерывность вероятностных мер. Теорема Радона-Никодима (теорема 31)

19. Теорема (32) о замене переменных под знаком интеграла Лебега. Теорема (33) Фубини.

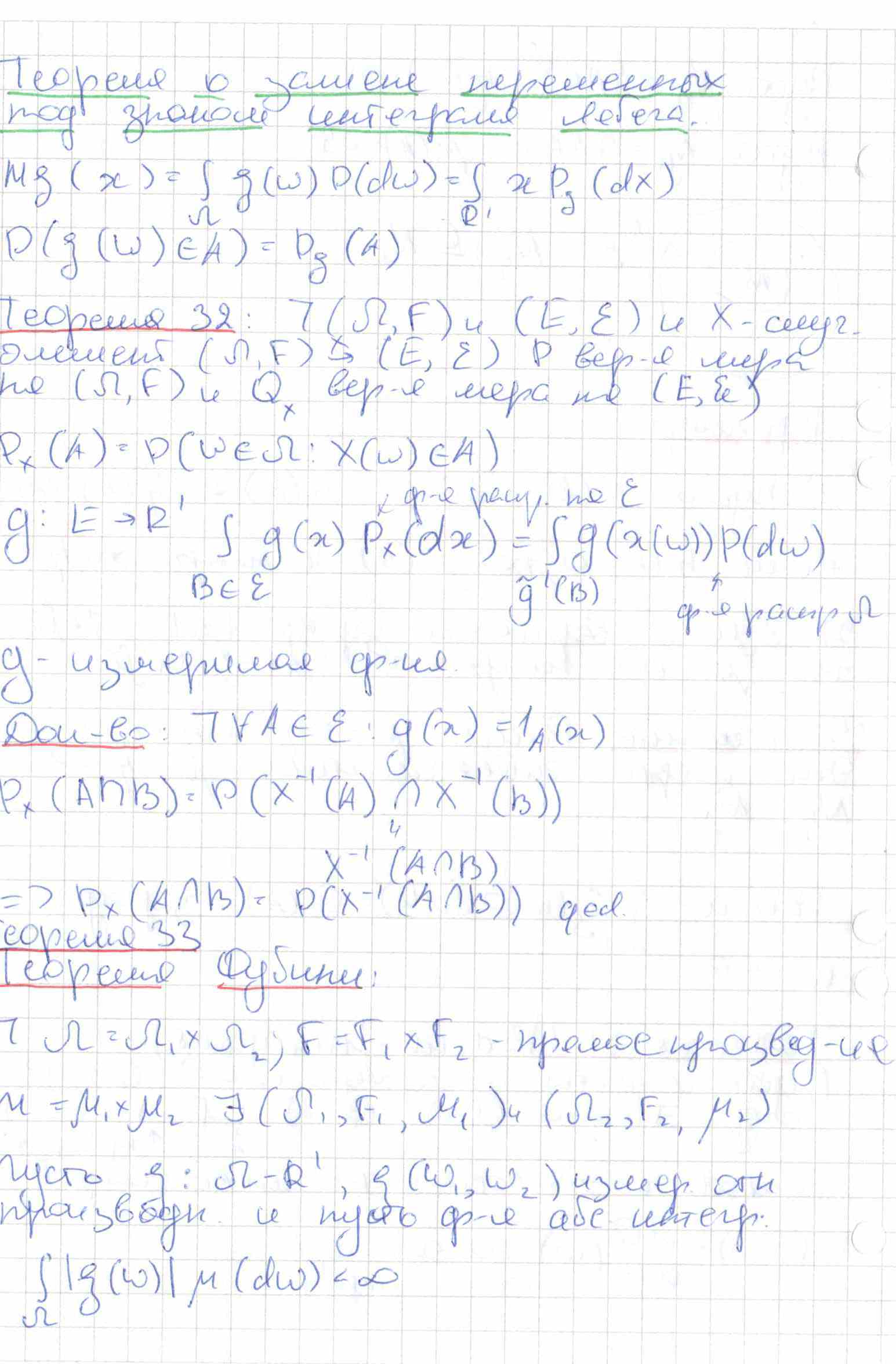
20. Условное математическое ожидание относительно σ-подалгебры (определение). Докажите существование и единственность условного математического ожидания (теорема 34).

21. Свойства условных математических ожиданий.

22. Условная вероятность. Регулярная условная вероятность.

23. Стохастический базис, согласованная последовательность, марковская последовательность, переходная вероятность (определения). Соотношение Чепмена-Колмогорова (теорема 37).

Пусть – измеримое пространство, кроме того, положим, что на выделено семейство алгебр {_n}_n>0 , обладающих свойствами:

а) для любого ;

б) для любых и ;

в)

Определение. Семейство алгебр на , обладающих свойствами а), б), в) будем называть потоком алгебр или фильтрацией. Измеримое пространство ( , ) с выделенной фильтрацией будем называть фильтрованным измеримым пространством и обозначать через ( , , ).

Определение. Фильтрованным вероятностным пространством или стохастическим базисом называется четверка ( , , , Р), где Р – вероятностная мера на фильтрованном измеримом пространстве, причем – пополнена множествами нулевой меры Р.

Замечание. Напомним, – пополнена множествами нулевой меры Р. Пусть любой элемент В , N_p {A F: P(A) = 0} и к В добавим N_p, т.е. . С помощью множеств построим новую алгебру, обозначаемую . Ясно, что содержит - алгебра, её называют пополнением относительно меры Р.

Определение. Будем говорить, что последовательность { со значениями в измеримом пространстве согласована с фильтрацией , если при каждом n она - измерима , т.е. { для любого В E, и для нее будем использовать обозначение ( , )_n>1.

Пусть на стохастическом базисе ( , , ,Р) задана согласованная последовательность { . Введем обозначения: а)  = алгебру, порожденную , б)  = , в) = эту алгебру называют обычно хвостовой.Очевидно, что - - измерима.

Определение. Последовательность ( , )_n>0 называется марковской, если Р - п. н. для любого

Р(В| ) = P(B| ), (1)

где .

Замечание. В силу теоремы 11 главы 1 (теоремы Бореля) существуют для борелевские функции , где и такие, что Р - п. н. Р(В| ) = , P(B| ) = . Поэтому (1) можно переписать в виде Р - п. н.

.

Определение. Пусть Р: , обозначаемая через P(s, ,t,B), s<t, называемая переходной вероятностью (вероятностью перехода) если :

1) при фиксированных s,t,B P( - измеримая функция;

2) при фиксированных s,t,x P( вероятностная мера на .

Определение. Будем говорить, что {Р(s, ,t,B)}-семейство переходных вероятностей марковского процесса ( , )_{t>0 ,}если Р(s, ,t,B) = P ) Р - п. н. для любых s,t,B.

Теорема 37 (Чепмен-Колмогоров). Пусть ( , )_t>0 – марковская последовательность, а {Р(s, ,t,B)} – соответствующее ей семейство переходных вероятностей. Тогда для любых справедливо равенство

Р(s, ,t,B) = . (2)

Доказательство. Пусть , тогда Р -п.н. Р(s, ,t,B) = P ) = P( ) = M( )=M[M( )| ]=M[P( )| ]= =M[P  ]= )P

Доказательство закончено.

24. Последовательность определенная рекуррентно. Теорема (38) о существовании и единственности последовательности определенной рекуррентно.

В данном пункте мы приведем методику непосредственного задания марковской случайной последовательности.

Пусть Ф: измеримая по Борелю функция, обозначаемая через Ф(t,x,y), где и – полные, сепарабельные, метрические пространства. Последовательность {X_t}_t>0 со значениями определим с помощью рекуррентного соотношения

, , (5)

где ( последовательность случайных элементов, принимающая значения в . Соотношение (5) называется процессом, определенным рекуррентно. Положим, что - нормированное пространство с нормой . Возникают два вопроса:

1) является ли X_t для любого t измеримым;

2) | Р - п. н.

Определение. Под сильным решением процесса, определенного рекуррентно, будем понимать последовательность измеримую относительно алгебры такую, что : а) Р( | )=1; б) она обращает (5) в тождество с вероятностью 1.

Определение. Будем говорить, что (5) имеет единственное сильное решение, если из того что существуют i=1,2 – два сильных решения соотношения (5), причем (т.е. они начинаются из одной точки), то Р( для любого

Теорема 38. Пусть Ф: , где – линейное нормированное пространство, удовлетворяющее условиям:

1) ||Ф(t,x,y) – Ф(t,z,y)||

2) ||Ф(t,0,y)|| .

Тогда: а) если выполнено 1), то решение (5) единственно; б) если выполнены 1) и 2) и Р - п. н. , то существует сильное решение (5).

Замечание 1. Поясним смысл условий теоремы 3. Очевидны неравенства:

||Ф(t,x,y)|| = ||Ф(t,0,y)+ Ф(t,x,y)- Ф(t,0,y)|| ||Ф(t,0,y)|| + ||Ф(t,x,y) - Ф(t,0,y)|| L+L||x|| = L(1+||x|| ) ( т.е. допустим рост по х не быстрее, чем линейный).

Доказательство. а) Пусть имеются два сильных решения, начинающихся на одной точке , имеем Р - п. н.

Значит, Р - п. н. для .

б) Заметим,

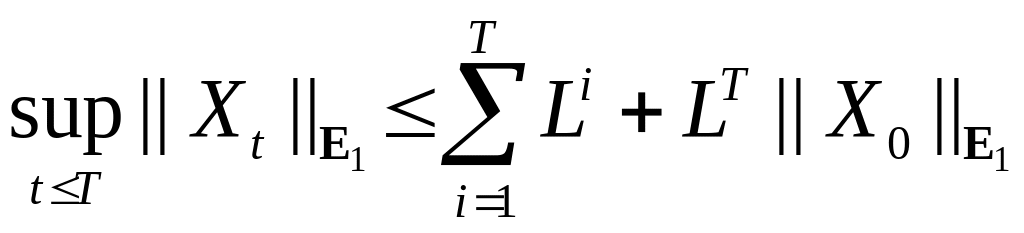Следовательно, если Р - п. н. – конечно, то Р-п. н.

Замечания. 1) Пусть удовлетворяет (5), и Если (5) имеет единственное сильное решение, то справедливо Р - п. н. для

2) Обозначим Р(s, ,t,B) = P(t, ,B) – переходную вероятность за один шаг. Из соотношения Чепмена-Колмогорова следует, чтобы построить переходную вероятность за t шагов, достаточно знать переходную вероятность за один шаг.

25. При выполнении каких условий последовательность определенная рекуррентно является Марковской (теорема 39). Примеры.

Установим условия, выполнение которых гарантирует, что процесс, определенный рекуррентно, является марковским.

Теорема 39. Пусть выполняются условия: 1) рекуррентное соотношение (5) имеет единственное сильное решение, 2) последовательность независимых в совокупности случайных величин (со значениями в ), 3) не зависит от . Тогда 1) последовательность - -измерима при каждом t и - марковская, 2) переходная вероятность за один шаг имеет вид

Доказательство. Нам надо доказать, что Р - п. н.

.

Рассмотрим сначала левую часть этого равенства в силу замечания 1.3.1 Р-п.н. = . Так как - сильное решение (5), то -измеримо, то по теореме Бореля для каждого t существуют функции такие, что Р - п. н. . Поэтому, в силу условий 2), 3) имеем Р - п. н.

= = =

= = .

Отсюда следует, что Доказательство закончено.

Примеры процессов, определенных рекуррентно.

1) Пусть =0, где -последовательность независимых (в совокупности) величин. В силу теоремы 4 является марковской последовательностью.

2) Дискретная модель диффузии. Рассмотрим рекуррентное соотношение:

, (6)

где - измеримые по Борелю функции, - последовательность независимых в совокупности случайных величин, причем . (6) имеет единственное сильное решение, если выполнены условия:

а)

б)

Пусть , а В этом случае удовлетворяет рекуррентному соотношению

, . (7)

Покажем, что , причем

, ;

Действительно. Обозначим , из рекуррентного соотношения (7) следует

М[ ]= = .

Ясно, что . Из определения дисперсии имеем . Получили рекуррентное соотношение для . Рассмотрим разность , имеем из (7): = =

Возведем в квадрат левую и правую части последнего равенства, а затем возьмем математическое ожидание от левой и правой частей, имеем из получившегося равенства:

=

Так как , то отсюда следует, что

.

Покажем, что - гауссовская последовательность. Доказательство проведём по индукции. Пусть - гауссовская случайная величина. Очевидно, что тоже гауссовская. Действительно, так как сумма двух гауссовских величин есть гауссовская величина, то гауссовская случайная величина. Таким образом основной шаг индукции установлен, а с ним доказано утверждение.