
- •Ответы к экзамену по курсу «Теория случайных процессов»
- •6. Задание вероятностной меры на (rт,b(rт)). Теорема Колмогорова (теорема 8 – без доказательства)
- •7. Определение случайной величины. Примеры. Разбиение. Дискретная(простая) случайная величина. Распределение вероятностей случайной величины.
- •2) Если случайная величина , то найдется последовательность простых случайных величин таких, что для всех .
- •10. Интеграл Лебега. Свойства математического ожидания.
- •12. Лемма Фату(теорема 16), теорема Лебега о мажорируемой сходимости (теорема 17). Равномерно интегрируемое семейство случайных величин. Критерий равномерной интегрируемости(теорема 19).
- •14. Сходимость в пространстве Lp, p принадлежит [1, ∞]. Критерий Коши(теорема 24).
- •16. Относительная слабая компактность семейства вероятностных мер. Теорема Прохорова (теорема 29)
- •26. Полумартингал (определения). Примеры
- •30. Мартингальные преобразования. Теорема Дуба-Мейера (теорема 50).
- •31. Последовательность имеющая ограниченную вариацию. Семимартингалы. Критерий того, что последовательность является семимартингалом (теорема 55).
- •32. Формула Ито для согласования случайных последовательностей (теорема 58). Формула Ито для произведения двух семимартингалов. Квадратическая и взаимная вариация (определения).
- •35. Разложение Куниты-Ватанабе (теорема 64).
- •36. Локальная плотность. Докажите, что локальная плотность является неотрицательным мартингалом (теорема 65).
- •37. Теорема (67) Гирсанова.
- •38. Однородная Марковская цепь. Классификация состояний однородной марковской цепи (теоремы 69-72)
- •2) Если - счетно, то классов не более, чем счетно.
- •40. Определение случайного процесса. Прогрессивно измеримый процесс. Достаточные условия существования прогрессивно измеримого процесса (теорема 76)
- •42. Пуассоновский случайный процесс (определение) и его свойства.
- •43. Полумартингалы (определения, случай непрерывного времени) Предопределенный процесс. Теорема (78) Дуба-Мейера. Пример.
- •44. Регулярные мартингалы. Критерий существования непрерывной справа модификации у равномерно интегрируемого супермартингала (теорема 79).
- •На лекциях была без доказательства!
- •48. Остановленный случайный процесс, локализующая последовательность, локальный полумартингал (непрерывное время).
- •49. Классификация марковских моментов опциональные, предсказуемые.
- •51. Процессы ограниченной вариации и их свойства (теоремы 94, 95).
- •52. Точечный случайный процесс (определение). Считающий процесс и его свойства. Компенсатор. Пример точечного процесса.
- •53. Интеграл Римана-Стильтеса (определение) и его свойства (теорема 96).
- •56. Интегрирование случайных процессов по мартингалами имеющим ограниченную вариацию (теорема 100).
- •57. Теорема Кэмбелла (следствие 101). Найдите характеристическую функцию Пуассоновского случайного процесса.
Ответы к экзамену по курсу «Теория случайных процессов»
2011/2012 учебный год. Лектор Хаметов В.М.
Измеримое пространство. Примеры измеримых пространств.
Определение .
![]() с
с
![]() алгеброй
F называется измеримым
пространством и обозначается (
,F).
алгеброй
F называется измеримым
пространством и обозначается (
,F).
Определение. Система F- подмножеств множества называется алгеброй, если:
она является алгеброй,
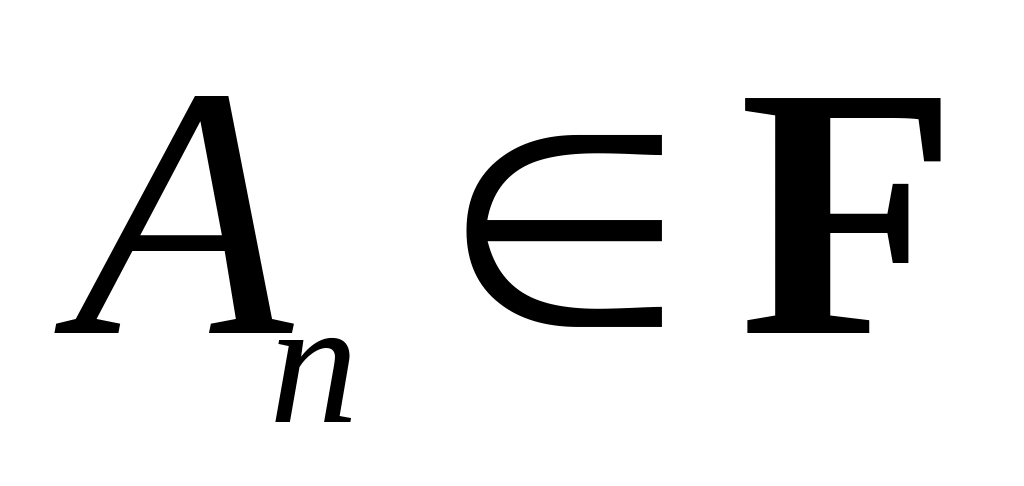 ,
для
,
для
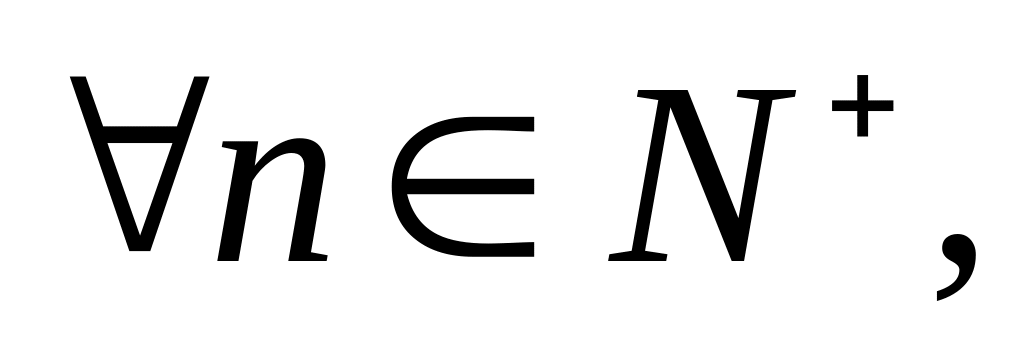 то
то
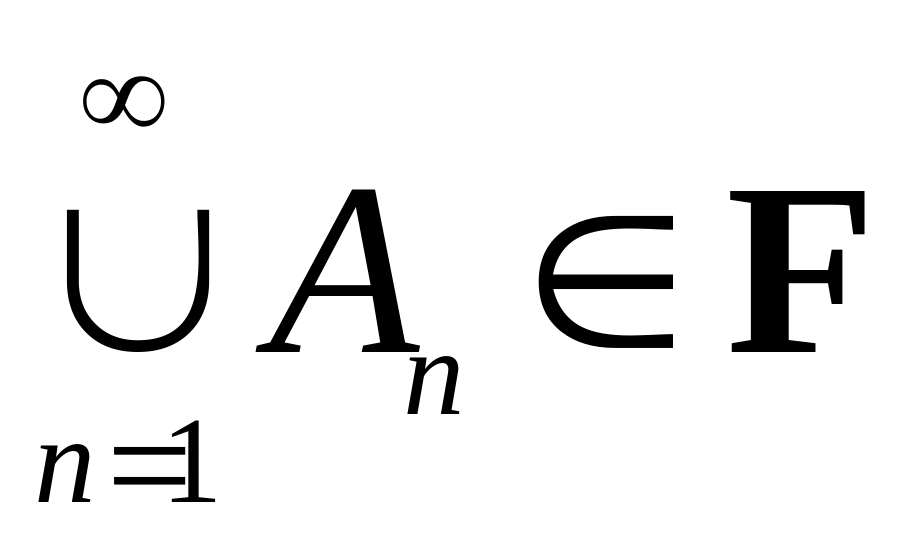 и
и
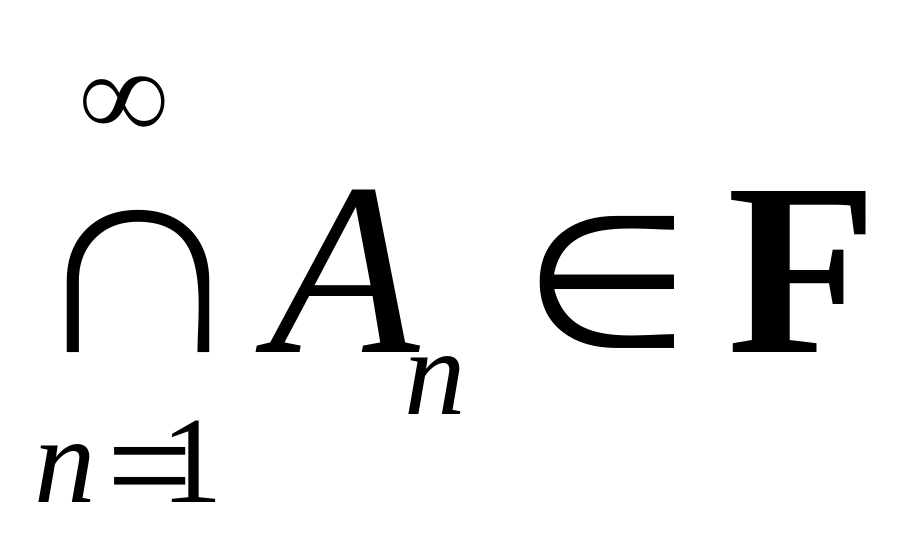 .
.
Определение. Пусть
![]() .
.
![]() -
система подмножеств множества
называется алгеброй если:
-
система подмножеств множества
называется алгеброй если:
а)
,
![]()
![]() ;
;
б)
![]() А
А![]() А
А![]() А
А![]() ;
;
в)
![]() А
А
![]() А
А
Примеры измеримых пространств
Измеримое пространство (R1, (R1))
Пусть R1=(-![]() ,
]
– действительная прямая и (a,b]
= {
,
]
– действительная прямая и (a,b]
= {![]() R1:
R1:
![]() }
для всех
}
для всех
![]() .
Обозначим через А(R1)
систему множеств в R1,
состоящую из конечных сумм непересекающих
интервалов вида (a,b]
:
.
Обозначим через А(R1)
систему множеств в R1,
состоящую из конечных сумм непересекающих
интервалов вида (a,b]
:
![]() А(R1),
где
А(R1),
где
![]() .
Нетрудно видеть, что эта система множеств,
а также
– образуют алгебру – А(R1)
, которая не является
.
Нетрудно видеть, что эта система множеств,
а также
– образуют алгебру – А(R1)
, которая не является
![]() алгеброй,
так как
алгеброй,
так как
![]() А(R1),
но
А(R1),
но
![]() А(R1).
А(R1).
Из предыдущих построений следует, что
(R1)
состоит из интервалов вида
![]() ,
где
,
где
![]() ,
и их счетных объединений и пересечений.
Отсюда следует, что:
,
и их счетных объединений и пересечений.
Отсюда следует, что:
i)
![]() ii)
ii)![]() iii)
iii)![]()
Измеримое пространство (Rn, (Rn))
Пусть Rn =
R![]() R
…
R
– называется прямое или декартово
произведение n
экземпляров числовой прямой, то есть,
множество упорядоченных наборов
R
…
R
– называется прямое или декартово
произведение n
экземпляров числовой прямой, то есть,
множество упорядоченных наборов
![]() ,
где
,
где
![]() ,
,
![]() .
.
Множество
![]() где
где
![]() ,
называется прямоугольником, то
есть,
,
называется прямоугольником, то
есть,
![]() Rn
:
Rn
:![]() , а
, а
![]() - его сторонами.
- его сторонами.
Через
![]() (Rn)
обозначим совокупность всех прямоугольников
из Rn.
(Rn)
- наименьшая
алгебра
порожденная
(Rn)
обозначим совокупность всех прямоугольников
из Rn.
(Rn)
- наименьшая
алгебра
порожденная
![]() - называется борелевской
алгеброй
множеств Rn,
которую и обозначим через
(Rn).
Измеримое
пространство (R
- называется борелевской
алгеброй
множеств Rn,
которую и обозначим через
(Rn).
Измеримое
пространство (R![]() ,
(R
))
,
(R
))
R
-
пространство числовых последовательностей
![]() где -
где -
![]() ,
,
![]() Пусть
Пусть
![]() - борелевское множество к-ой числовой
прямой (то есть, множество
- борелевское множество к-ой числовой
прямой (то есть, множество
![]()
(R1)). Рассмотрим
множества :
(R1)). Рассмотрим
множества :
i)
![]() R
R
![]() :
:![]() };
};
ii)
![]() R
:
R
:![]() };
};
iii)
![]() (R
(R
![]() )
)
![]() R
:
R
:
![]() .
.
Такие множества называются цилиндрическими,
причем
![]() называют основанием цилиндра, а
остальные координаты – образующими
цилиндра. Нетрудно видеть, что множества
называют основанием цилиндра, а
остальные координаты – образующими
цилиндра. Нетрудно видеть, что множества
![]() ,
,
![]() ,
,
![]() образуют алгебру. Обозначим наименьшие
алгебры, порожденные множествами вида
i)-iii) через
(R
),
1(R
),
2(R
),
соответственно. Можно показать, что эти
алгебры
совпадают.
образуют алгебру. Обозначим наименьшие
алгебры, порожденные множествами вида
i)-iii) через
(R
),
1(R
),
2(R
),
соответственно. Можно показать, что эти
алгебры
совпадают.
Измеримое пространство (RТ , (RТ))
Пусть Т![]() – произвольное пространство, множество.
Пространство RТ
– совокупность действительных функций
на T со значениями в R1,
обозначенные
– произвольное пространство, множество.
Пространство RТ
– совокупность действительных функций
на T со значениями в R1,
обозначенные
![]() .
Для простоты будем считать, что
.
Для простоты будем считать, что
![]() .
Обозначим:
.
Обозначим:![]() ,
где
,
где
![]() .
Проводя рассуждения аналогичные
приведенным в пункте 2.3, легко построить
алгебру
борелевских множеств на RТ,
порожденную цилиндрическими множествами
.
Проводя рассуждения аналогичные
приведенным в пункте 2.3, легко построить
алгебру
борелевских множеств на RТ,
порожденную цилиндрическими множествами
![]() и
обозначаемую через (RТ).
и
обозначаемую через (RТ).
Возникает вопрос: какова структура
множества
(RТ)?
Оказывается, что любое множество
(RТ) допускает
представление
![]() ,
где
,
где
![]() (R
(R![]() ).
Отсюда следует, что множества, зависящие
от поведения функций в несчетном числе
точек t
).
Отсюда следует, что множества, зависящие
от поведения функций в несчетном числе
точек t
![]() Т
необязаны быть измеримыми относительно
(RТ).
Например: i)
Т
необязаны быть измеримыми относительно
(RТ).
Например: i)![]()
![]() },
},
![]()
![]() ,
ii)
,
ii)![]()
![]() - непрерывные в точке
- непрерывные в точке
![]() .
.
В связи с неизмеримостью некоторых множеств из RТ по отношению к (RТ) естественно рассматривать более узкие функциональные пространства.
Измеримое пространство (С[0,T], (С[0,T])).
Пусть Т=[0,1], С[0,1] - пространство
непрерывных функций xt,
t
[0,1], со значениями в R1.
Очевидно, С[0,1] –метрическое
пространство, относительно метрики
ρ(х,у)=
![]()
![]() ,
то есть ρ(х,у) – расстояние между
двумя непрерывными функциями, обладающие
свойствами:
,
то есть ρ(х,у) – расстояние между
двумя непрерывными функциями, обладающие
свойствами:
ρ (х,у)=0
 x=y;
2) ρ (х,у)= ρ (у,x);
3) ρ (х,у)
x=y;
2) ρ (х,у)= ρ (у,x);
3) ρ (х,у) ρ (x,z)+
ρ(z,y).
ρ (x,z)+
ρ(z,y).
Через (С[0,T]) обозначим наименьшую алгебру, порожденную цилиндрическими множествами, которые строятся аналогично пункту (RТ , (RТ)).
Измеримое пространство (,()).
– пространство функций xt , t [0,1], со значениями в R1 , непрерывные справа, имеющие пределы слева в любой точке t [0,1]. В нем также можно ввести метрику:
ρs(x,y)![]() inf
{
inf
{![]() ,
где
,
где
![]() - множество строго возрастающих
непрерывных на отрезке [0,1] функций
- множество строго возрастающих
непрерывных на отрезке [0,1] функций
![]() ,
причем
,
причем
![]() и
и
![]() }.
}.
![]() -алгебра
() строится аналогично пункту (RТ
, (RТ)).
-алгебра
() строится аналогично пункту (RТ
, (RТ)).
2. Задание вероятностной меры на (R1,B(R1)). (теорема 4) Классификация мер на (R1,B(R1)).
Измеримое пространство (R1,(R1)).
Пусть F: R1![]() [0,1]
- измеримая функция, обладающая свойствами:
[0,1]
- измеримая функция, обладающая свойствами:
1) неубывающая;
2) F(-
)=0
F(
)=1,
где F(-
)=![]() и F(
)=
и F(
)=![]() ;
;
3) непрерывна справа и имеет предел слева в каждой точке R1.
Определение. Всякая функция F(x), удовлетворяющая свойствам 1)- 3) называется функцией распределения на R1 .
Теорема 4.
Пусть
![]() -
функция распределения на R1,
тогда на (R1,
(R1))
существует и притом единственная
вероятностная мера Р такая, что для
любых
-
функция распределения на R1,
тогда на (R1,
(R1))
существует и притом единственная
вероятностная мера Р такая, что для
любых
![]() ,
причем
,
причем
![]() ,
Р
,
Р![]()
Пример: пусть функция распределения имеет вид:
![]() =
=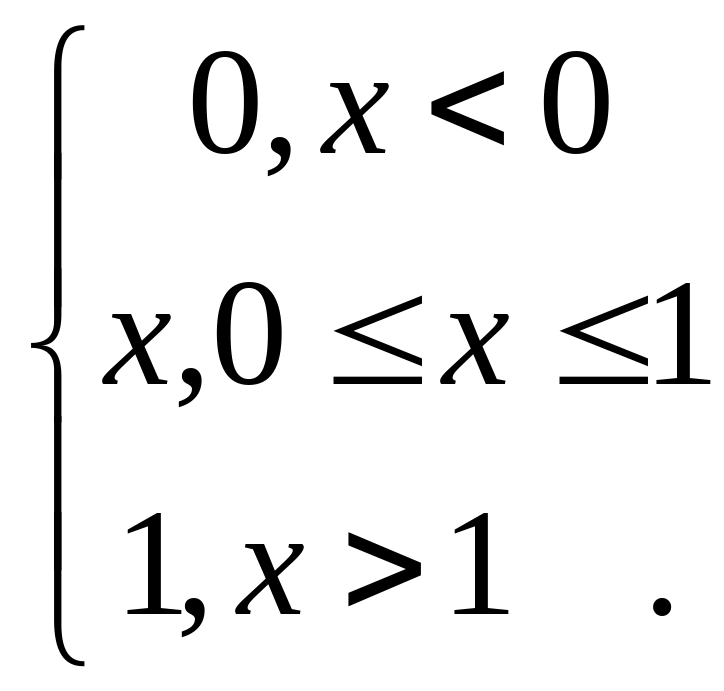
Соответствующую ей меру называют мерой
Лебега отрезка
![]() и обозначают Λ, причем Λ
и обозначают Λ, причем Λ![]()
Приведем классификацию мер на (R1, (R1)).
Дискретные меры.
Пусть
-
функция распределения кусочно-постоянна
и меняет свои значения в точках
![]() х1,х2,
…, причем
х1,х2,
…, причем
![]() где
где
![]() Ясно, что соответствующая этой функции
распределения вероятностная мера Р
сосредоточена в точках х1,х2,
…, причем Р
Ясно, что соответствующая этой функции
распределения вероятностная мера Р
сосредоточена в точках х1,х2,
…, причем Р![]()
![]() .
.
Набор чисел
![]() где
где
![]() -
называется дискретным распределением.
-
называется дискретным распределением.
Примеры дискретных распределений содержатся в приведенной ниже таблице.
Распределение |
|
Параметры |
1. Дискретное равномерное |
|
|
2. Бернулли |
|
|
3. Биноминальное
|
|
|
4. Пуассоновское Пк |
Пk |
|
5. Геометрическое = |
|
|
6. Отрицательное биноминальное
|
|
|
Абсолютно непрерывные меры.
Пусть существует неотрицательная
функция
![]()
![]() такая, что функция распределения
такая, что функция распределения
![]() допускает представление:
допускает представление:
![]()
Функцию
![]() (
)
называют плотностью функции
распределения
.
(
)
называют плотностью функции
распределения
.
Пример: Функцию
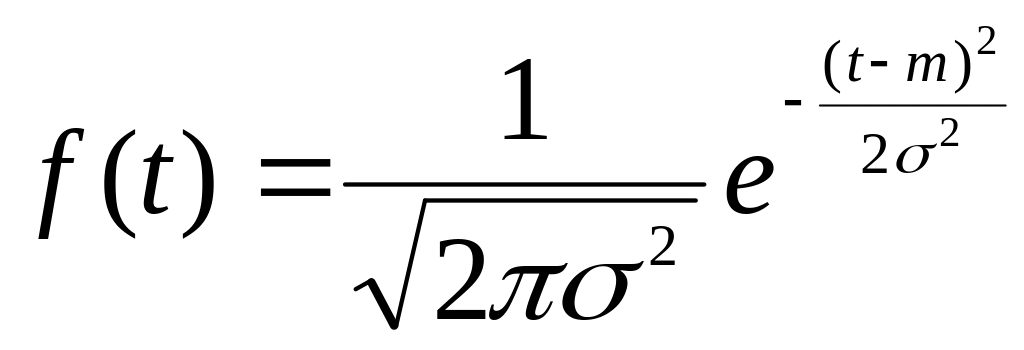 ,
называют гауссовской плотностью.
Легко убедиться в том, что
,
называют гауссовской плотностью.
Легко убедиться в том, что
![]()
Сингулярные распределения.
Определение. Точка
![]() называется
точкой роста функции распределения
,
если
называется
точкой роста функции распределения
,
если
![]() для любого
для любого
![]() .
.
Определение. Сингулярными мерами называются меры, функции распределения которых непрерывны, причем точки роста, которые образуют множество нулевой меры Лебега.
Пример. Возьмем отрезок
![]() и построим на нем сингулярную функцию
распределения
с помощью приема, принадлежащего Кантору
Г. Пусть Fo
– функция распределения, соответствующая
мере Лебега на отрезке [0,1].Разделим
на 3 равные части и определим - функцию
распределения
и построим на нем сингулярную функцию
распределения
с помощью приема, принадлежащего Кантору
Г. Пусть Fo
– функция распределения, соответствующая
мере Лебега на отрезке [0,1].Разделим
на 3 равные части и определим - функцию
распределения![]() следующим образом:
=
0, при x < 0;
=
следующим образом:
=
0, при x < 0;
=
![]() x,
при x
[0,
x,
при x
[0,![]() );
=
);
=
![]() ,
при x
[
,
при x
[![]() ,
,![]() );
=
x
–
,
при x
[
);
=
x
–
,
при x
[![]() ,1);
=
1, при x > 1. Затем, каждый
из интервалов
,1);
=
1, при x > 1. Затем, каждый
из интервалов
![]() и
и
![]() опять поделим на 3 равные части и определим
функцию распределения
опять поделим на 3 равные части и определим
функцию распределения
![]() следующим образом:
следующим образом:
=
0, при x < 0;
=
![]() x,
при x
[0,
x,
при x
[0,![]() );
=
);
=
![]() при x
[
,
при x
[
,![]() ];
=
];
=
![]() x
-
,
при x
[
,
x
-
,
при x
[
,![]() ];
=
];
=
![]() при x
[
,
);
=
x
– 1, при x
[
при x
[
,
);
=
x
– 1, при x
[![]() ,
,![]() );
=
);
=
![]() при x
[
,
при x
[
,![]() );
=
x
-
);
=
x
-
![]() ,
при x
[
,1].
,
при x
[
,1].
Продолжая этот процесс далее мы построим
последовательность функции распределения
![]() ,
которая, очевидно, сходится при
,
которая, очевидно, сходится при
![]() к некоторой неубывающей непрерывной
функции распределения
.
Очевидно, что точки роста функции
распределения
имеет нулевую меру Лебега, так как общая
длина интервалов, на которых
принимает постоянные значения равна
1. Действительно, общая длина интервалов
постоянства функции
равна
к некоторой неубывающей непрерывной
функции распределения
.
Очевидно, что точки роста функции
распределения
имеет нулевую меру Лебега, так как общая
длина интервалов, на которых
принимает постоянные значения равна
1. Действительно, общая длина интервалов
постоянства функции
равна
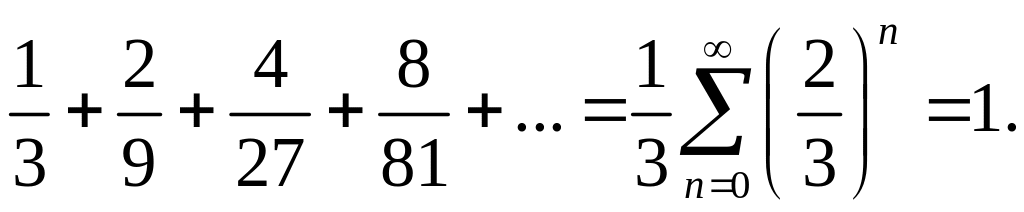
Пусть
![]() -
множество точек роста функции
распределения
,
тогда из последнего рассуждения следует,
что
-
множество точек роста функции
распределения
,
тогда из последнего рассуждения следует,
что
![]() (в этих случаях говорят, что мера,
соответствующая этой функции распределения
сингулярна по отношению к мере Лебега
).
(в этих случаях говорят, что мера,
соответствующая этой функции распределения
сингулярна по отношению к мере Лебега
).
3. Теорема Лебега (теорема 5). Функция распределения.
Теорема 4.(Лебега) Любая функции распределения на прямой R1 представима в виде:
![]() ,
,
где
![]() и
и
![]() ,
а
-
дискретная,
-
абсолютно непрерывная,
,
а
-
дискретная,
-
абсолютно непрерывная,
![]() -
сингулярная функции распределения.
-
сингулярная функции распределения.
Пусть F: R1 [0,1] - измеримая функция, обладающая свойствами:
1) неубывающая;
2) F(- )=0 F( )=1, где F(- )= и F( )= ;
3) непрерывна справа и имеет предел слева в каждой точке R1.
Определение. Всякая функция F(x), удовлетворяющая свойствам 1)- 3) называется функцией распределения на R1 .
4. Задание вероятностной меры на (Rn,B(Rn))(теорема 6). Примеры.
Измеримое пространство (Rn ,(Rn)).
Пусть
![]() - измеримая функция, непрерывная справа
(по совокупности измененных), имеющая
левый предел. Введем оператор
- измеримая функция, непрерывная справа
(по совокупности измененных), имеющая
левый предел. Введем оператор
![]()
![]() ,
действующей по правилу
,
действующей по правилу
![]() .
.
Определение. Всякая непрерывная справа функция удовлетворяющая условиям:
1)
![]() для любых
для любых
![]() ,
i =
,
i =
![]() ;
;
2)
![]() ;
;
3)
![]() ,
если хотя бы одна из координат n-мерного
вектора
,
если хотя бы одна из координат n-мерного
вектора
![]() принимает
значение
принимает
значение
![]() ,
,
называется
![]() -мерной
функцией распределения.
-мерной
функцией распределения.
Очевидно следующее утверждение.
Теорема 6. Пусть
![]() -
-мерная
функция распределения. Тогда на (Rn,(Rn))
существует единственная вероятностная
мера Р такая, что
-
-мерная
функция распределения. Тогда на (Rn,(Rn))
существует единственная вероятностная
мера Р такая, что
![]() , где
, где
![]() ,
,
![]() .
.
Примеры. 1) Пусть
![]() =
=![]()
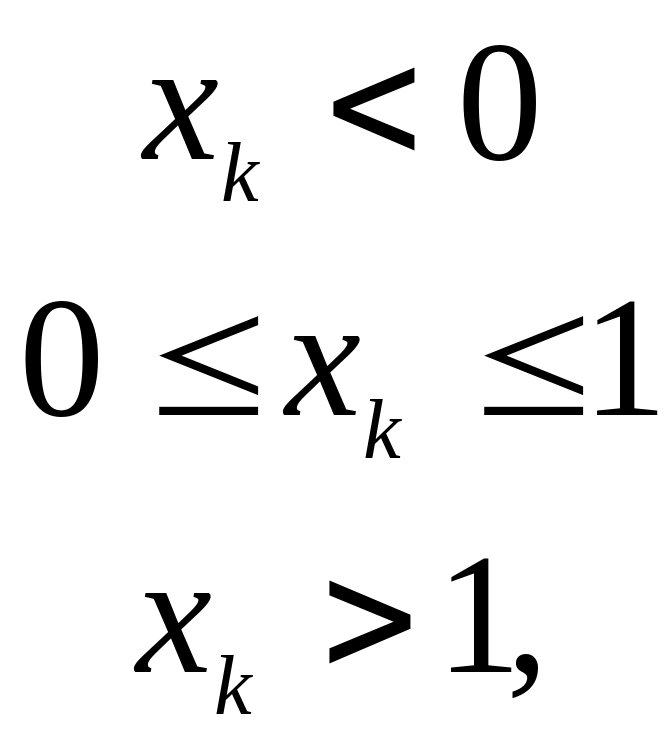
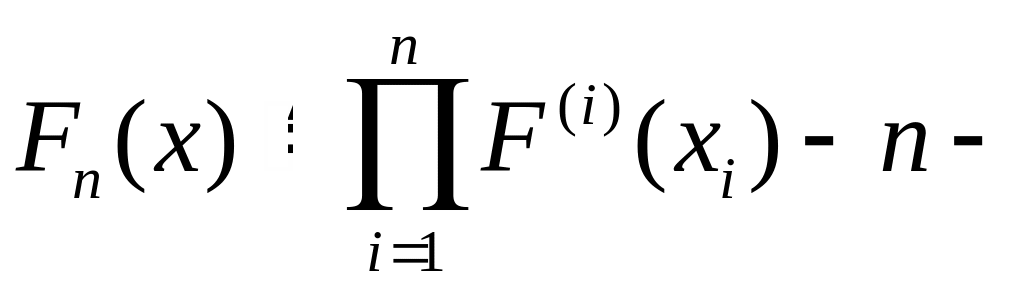 мерная
функция распределения вероятностей,
которой соответствует мера Лебега
на
мерная
функция распределения вероятностей,
которой соответствует мера Лебега
на
![]() .
.
2)
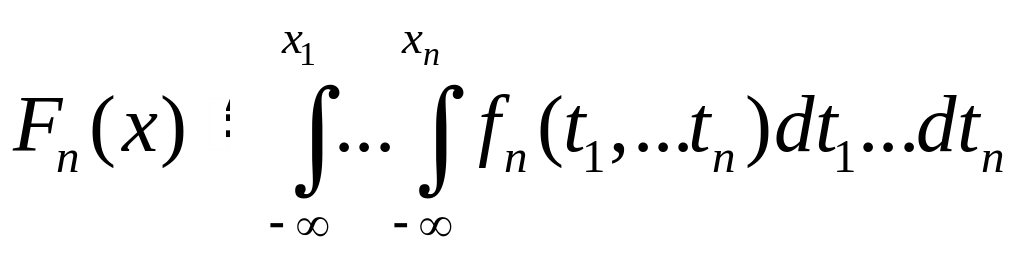 ,где
,где
![]() .
.
5. Задание вероятностной меры на (R∞,B(R∞))(теорема 7)
Измеримое пространство (R ,(R ))
Обозначим через
![]() R
:(
R
:(![]() )
)![]() ,
где
,
где
![]() Rn
– цилиндрическое множество в
Rn
– цилиндрическое множество в
![]() с
основанием
с
основанием
![]() (Rn).
Пусть последовательность вероятностных
мер
(Rn).
Пусть последовательность вероятностных
мер
![]() определенных, соответственно, на (R1
,(R1)),
(R2 ,(R2)),
обладает следующим свойством:
определенных, соответственно, на (R1
,(R1)),
(R2 ,(R2)),
обладает следующим свойством:
![]() (1)
(1)
где
![]() ,
,
![]() .
.
Условие (1) называют условием (свойством) согласованности.
Теорема 7.
(Колмогорова о продолжении вероятностной
меры на (R
,(R
)).
Пусть
![]() - последовательность вероятностных
мер, соответственно, на (R1,(R1)),
(R2,(R2)),
обладающая свойством согласованности.
Тогда существует единственная мера Р
на (R
- последовательность вероятностных
мер, соответственно, на (R1,(R1)),
(R2,(R2)),
обладающая свойством согласованности.
Тогда существует единственная мера Р
на (R![]() ,(R
))
такая, что для каждого
,(R
))
такая, что для каждого
![]() P
P![]() P
P![]() для
.
для
.
