26. Полумартингал (определения). Примеры
Пусть (
,
,
,Р)
– стохастический базис, последовательность
{
- согласована с потоком
,
и принимает значения в
.
Определение. Последовательность
(
,
)t>1
называется мартингалом, если:
1)
,
2)
Если выполнено 1) и
Р -п. н., то последовательность
(
,
)t>0
называется супермартингалом.
Если выполнено 1) и
Р - п. н., то последовательность (
,
)t>0
называется субмартингалом.
Пример. Пусть
,
где
независимые в совокупности случайные
величины. Пусть
,
.
Ясно, что
=
=
+
+
+
.
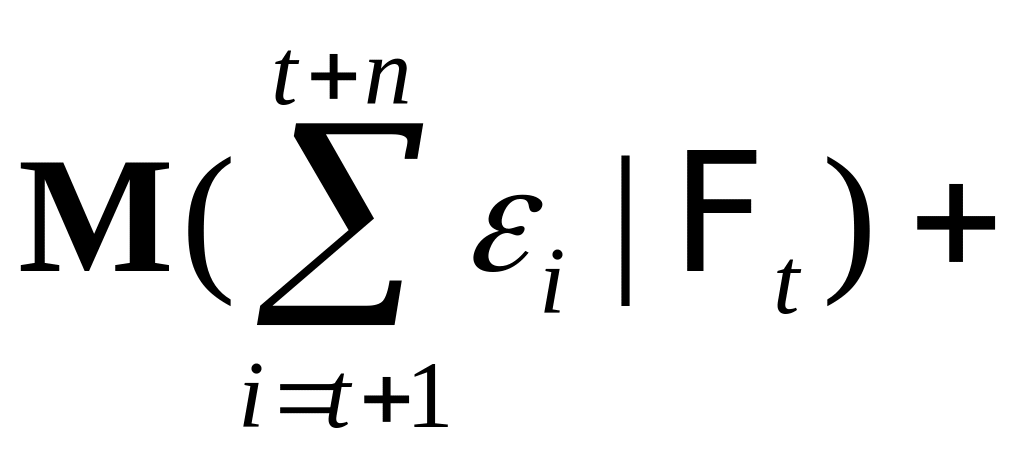Отсюда следует, что:
а) (
,
)t>1-
мартингал, если
для
любого t;
б) (
,
)t>1-
супермартингал, если
для
любого t;
в) (
,
)t>1-
субмартингал, если
для
любого t;
27. Теорема (40) Дуба о существовании конечного предела у неотрицательного однородного мартингала.
Теорема
40 (Дуба). Пусть (
,
)t>0
– неотрицательный супермартингал,
тогда с вероятностью 1 существует
.
Замечания.
1) Покажем, что предложения о неотрицательности
супермартингала (
,
)t>0
можно отказаться. Очевидно, что М
М
,
т.е. в среднем последовательность
-
убывает. Пусть
Образуем новую последовательность
.
Понятно, что
.Тогда
,
значит любой супермартингал представим
в виде разности двух неотрицательных
супермартингалов.
2) Если
- супермартингал, то
- субмартингал. Поэтому утверждение
теоремы 6 верно и для субмартингалов.
Доказательство теоремы Дуба опирается на две вспомогательные леммы.
Пусть
числовая
последовательность, a<b,
[a,b]
– отрезок. Обозначим
- число пересечений отрезка [a,b]
последовательностью
снизу вверх.
Лемма 41 (О числе пересечений отрезка [a,b] снизу вверх).
Справедливо неравенство:
,
где
Доказательство. Обозначим
,
,
,
,
,
Очевидно, что
Отсюда следует, что
(b-a)
=
.
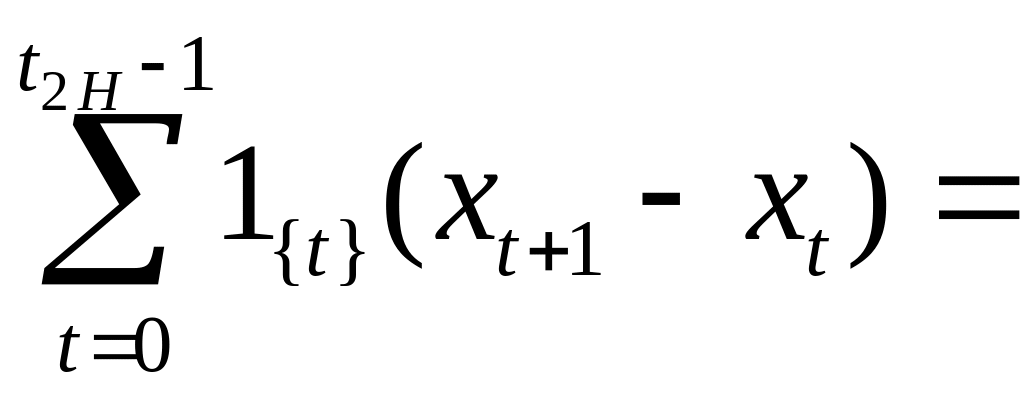
Докзательство закончено.
Лемма 42. (О среднем числе пересечений).
Пусть (
,
)t>0–
неотрицательный супермартингал, тогда
М
.
Доказательство. В силу леммы 7 имеем неравенство:
.
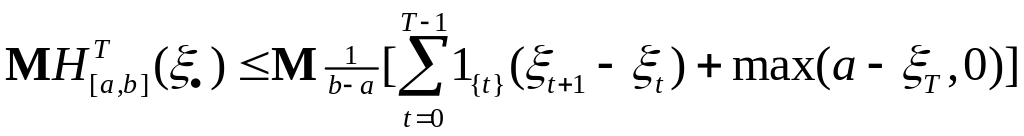Так как (
,
)t>0
- супермартингал, то М(
)
≤ 0. Отсюда следует неравенство
.
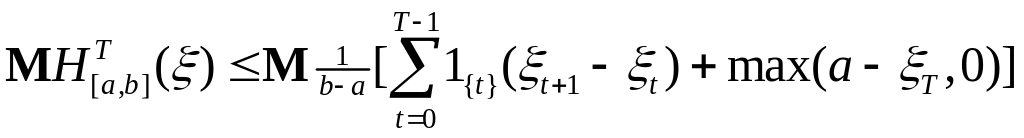
Доказательство закончено.
Доказательство теоремы 40. Предположим,
что у последовательности
не существует конечного предела. Через
В обозначим множество
не имеет конечного предела}. Наше
предположение выполнено, если:
1)
Р - п. н.,
2)
Р - п. н.
Обозначим: А
},
C=
}.
Очевидно, что
,
поэтому
.
Значит для доказательства теоремы
достаточно доказать, что Р(А) =0
и Р(С)=0.
Покажем, что Р(А)=0. В силу
неравенства Чебышева и леммы Фату имеем
Р(
.
Устремляя теперь
,
получаем Р(А)=0.
Теперь докажем, что Р(С)=0. Заметим, что
,
где
и
- рациональные числа}=
=
.
Рассмотрим вероятность Р(
N)
в силу неравенства Чебышева и леммы 8
мы имеем:
Р(
N)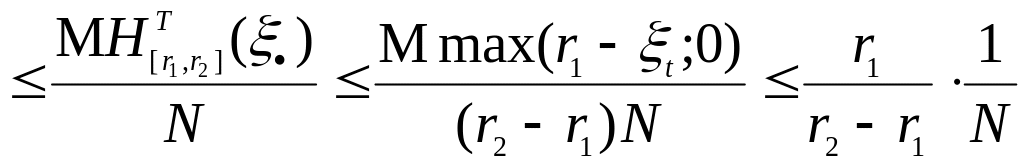
.
Устремляя
теперь
,
получаем неравенство
Р(
N)
.
Отсюда следует, что Р(
,
т.е.Р(С)=0. Доказательство закончено.
28. Равномерно интегрируемые мартингалы. Марковские моменты. Примеры марковских моментов. Свойства марковских моментов.
Определение. Мартингал
называется равномерно интегрируемым,
если
.
Теорема 43. Пусть
равномерно интегрируемый мартингал,
тогда Р -п.н. существует случайная
величина
такая, что:
а)
=
Р - п. н.,
б)
М|
-
Р - п. н.
Определение. Отображение
называется марковским моментом,
если
для
.
Конечный марковский момент (Р(
)=1)
называется моментом остановки.
Обозначим
для
всех
}.
Примеры: 1)
.
2)
Пусть
- случайная последовательность, а
-марковский момент. Определим
,
где
Тогда
измерима.
(Докажите самостоятельно).
3) Пусть
марковский
момент. Действительно:
.
Предложение 44. Пусть
марковский
момент. Тогда 1)
,
2)
Доказательство. 1) Очевидно
.
Поэтому из определения марковского
момента следует, что
.
Второе утверждение очевидно.
4.2. Пусть
марковский
момент относительно фильтрации
.
Предложение
45. 1) Если ,
- марковские
моменты, то
min(,),
max(,),
+,
(-)+
max(-,0)
являются марковскими моментами.
2) Если
- марковские моменты и
Р - п. н., то
.
3) Если
- марковские моменты, то
принадлежат
и
.
4) Если
- последовательность марковских моментов.
Тогда
n
,
n
,
n
,
n
,
n
также являются марковскими моментами.
29. Остановленная последовательность. Локализующая последовательность марковских моментов. Локальные полумартингалы. Мартингал – разность. Докажите, что всякий локальный мартингал является супермартингалом (теорема 49).
Определение.
Последовательность
называется
остановленной, если
Определение.
Последовательность марковских моментов
называется -локализующей,
если она неубывающая и Р - п. н.
существует
=
n
. Если
,
то
называется локализующей.
Определение.
Последовательность
называется локальным полумартингалом,
если существует локализующая
последовательность
,
такая, что остановленная последовательность
является полумартингалом.
Определение.
Последовательность
называется мартингал-разностью,
если существует М(t
|
)
для любого
и М(
)=0
Р - п. н.
Из этого определения следует утверждение.
Предложение
13. Последовательность
,
где
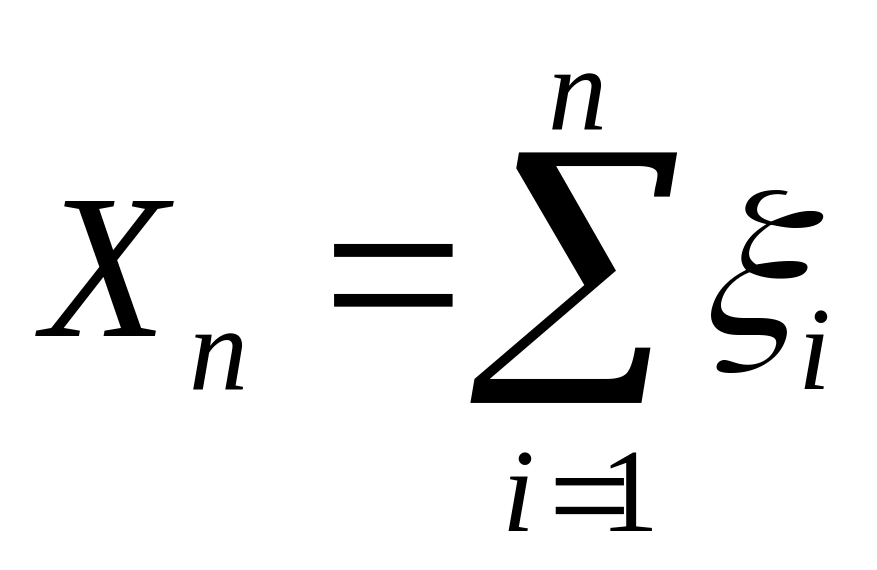является мартингалом (относительно
меры Р) тогда и только тогда, когда
является мартингал разностью.
Теорема 16. Пусть - локальный мартингал (относительно меры Р). Тогда последовательность является супермартингалом (относительно меры Р).
Доказательство.
В силу условий существует локализующая
последовательность марковских моментов
такая, что
P
- п. н., причем
Р - п. н. Поэтому в силу леммы Фату,
имеем P - п. н.
=
=
M(
|
)
=
=
.
Доказательство закончено.