10. Интеграл Лебега. Свойства математического ожидания.
Пусть (
,F,P)
- конечное вероятностное пространство,
т.е. существует набор множеств
таких, что
при
и
,
а
-
простая случайная величина.
Определение. Математическим
ожиданием простой случайной величины
,
обозначаемым через М
,
называется величина M
P(Ak).
Это определение корректно, так как оно
не зависит от способа представления
случайной величины
.
Для математического ожидания будем
использовать следующее обозначение:
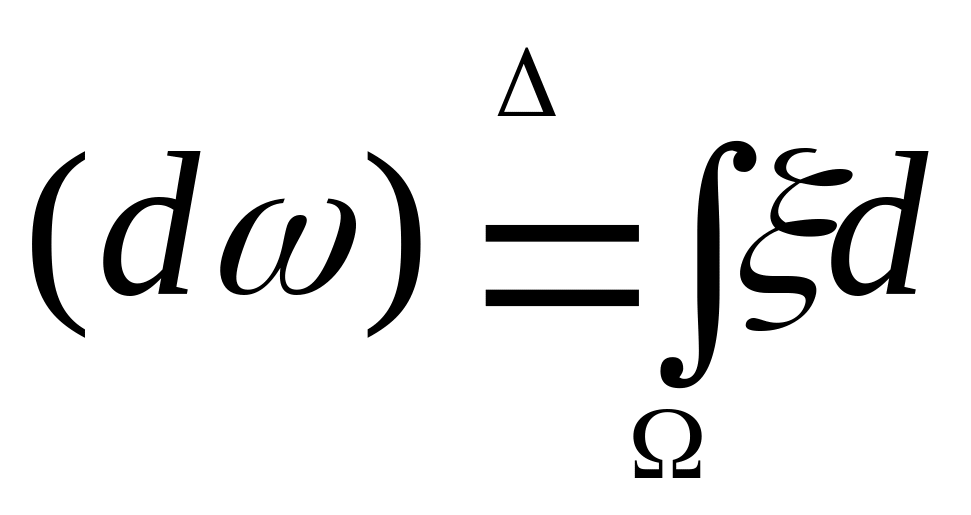P
P.
Определение. Интеграл Лебега
относительно вероятностной меры Р
случайной величины
,
обозначаемый М
,
определяемый равенством M
M
называется математическим ожиданием
случайной величины
.
Это определение будет корректным, если
значение предела не зависит от способа
выбора аппроксимирующей последовательности
(иначе говоря, если
и
,
то
M
=
M
).
Пусть теперь
- произвольная случайная величина.
Обозначим
.
Определение. Говорят, что математическое
ожидание
случайной величины
существует, если хотя бы одна из величин
или
конечна, т.е.
.
В этом случае по определению полагается
,
а
- называется интеграл Лебега от
по мере Р.
Определение. Говорят, что математическое
ожидание случайной величины
конечно, если
и
.
Отсюда следует, что
- конечно тогда и только тогда, когда
.
Наряду с
можно
рассматривать и
,
если они определены, то их называют
моментами
-
порядка, где r = 1,2,…,k.
Свойства математического ожидания.
А) Пусть
и у случайной величины
существует
,
тогда существует
и
.
Доказательство. Для простых функций
это утверждение очевидно. Пусть
,
где
-
простые случайные величины и
,
следовательно
.
Значит
.
В) Пусть
,
тогда
.
С) Если существует
,
то
.
Доказательство. Так как
,
то из А) и В) следует, что
,
то есть
.
D) Если существует
,
то для каждого A
F
существует
.
Если
конечно, то
- конечно.
Доказательство следует из пункта
В), так как
,
.
Е) Если
и
- случайные величины, причем
и
,
то
.
Доказательство. Пусть
и
- последовательность простых функций
таких, что
и
.
Тогда
и
.
Кроме того
и
.
Значит
.
F) Если
,
то
.
G) Если
,
Р-п.н. и
,
то
и
.
Доказательство. Пусть
,
тогда
,
где
.
В силу Е)
.
Н) Пусть
и
,
тогда
Р - п.н.
Доказательство. Обозначим
.
Очевидно, что
.
поэтому в силу свойства В)
,
следовательно
,
значит
для всех
,
но
.
I) Пусть
и
- случайные величины такие, что
и
и для всех
.
Тогда
Р - п.н..
Доказательство. Пусть
.
Тогда
.
Поэтому
,
тогда по свойству Е)
,
а в силу Н)
P - п.н., значит Р(В)=0.
J) Пусть
-
расширенная случайная величина и
,
тогда
P
- п.н..
Доказательство. Действительно,
пусть
и Р(А) > 0. Тогда
,
что противоречит предположению
.
11. Сходимость по вероятности и с вероятностью один случайных величин. Теорема о монотонной сходимости (теорема 15).
Пусть
на
задано
последовательность
случайных величин.
Определение.
Последовательность случайных величин
называется сходящейся по вероятности
к случайной величине
,
обозначается
или
,
если для
при
.
Теорема
13. Последовательность
случайных величин
сходится по вероятности к случайной
величине
тогда и только тогда, когда
при
.
Определение. Последовательность
случайных величин
называется сходящейся с вероятностью
1 к случайной величине
,
если
,
обозначается
.
Лемма
14. (Бореля-Кантелли)
Пусть
последовательность событий и
.
Если
,
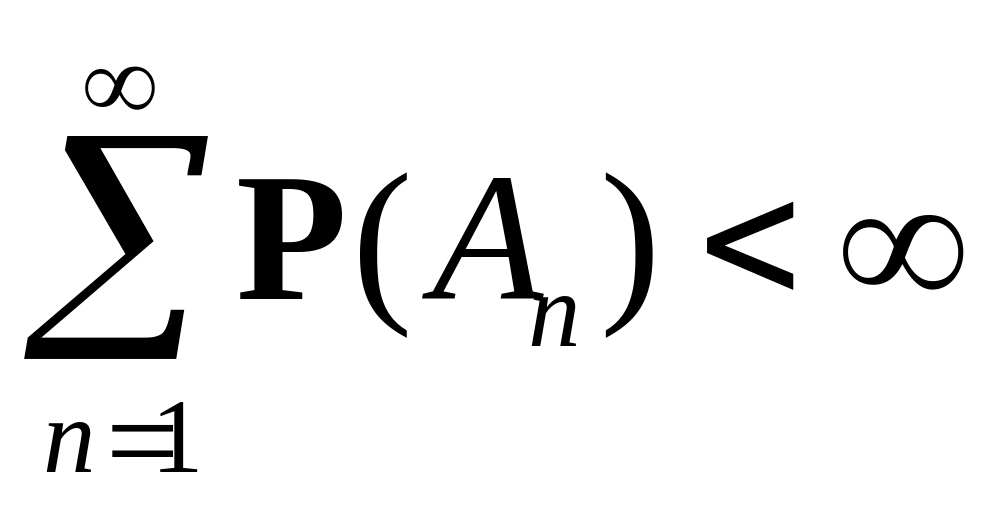то Р(А) = 0.
Доказательство. В силу свойства вероятности имеем
Р(А)
=
.
Доказательство закончено.
Теорема
15 (О монотонной сходимости) Пусть
случайные величины. Тогда справедливы следующие утверждения:
а) если
;
б) если
.
Доказательство.
а) Предположим, что
.
Пусть для каждого
- последовательность простых случайных
величин таких, что
при
.
Обозначим
.
Тогда очевидно, что
.
Пусть
,
поскольку для
,
то переходя к пределу при
получим, что для любого
,
значит
.
Так как случайные величины
простые и
,
то
.
С другой стороны, очевидно, что
.
Поэтому
,
значит
=
.
Пусть теперь
- случайная величина с
.
Если
,
то в силу свойства В) математических
ожиданий
=
,
утверждение доказано.
Пусть
,
тогда вместе с условием
получаем:
.
Очевидно, что
для всех
.
Поэтому, согласно доказанному
и значит по свойству Е) математических
ожиданий
.
Так как
,
то
при
.
Доказательство пункта б) следует из а), если вместо исходных случайных величин рассмотреть случайные величины со знаком минус.