56. Интегрирование случайных процессов по мартингалами имеющим ограниченную вариацию (теорема 100).

Пусть - мартингал, имеющий интегрируемую вариацию. Пусть - ограниченный предсказуемый случайный процесс. Тогда определен P- п. н. интеграл Римана - Стилтьеса от предсказуемой функции  по мартингалу m: , где - разбиение отрезка , такое, что при . Из этого построения следует, что 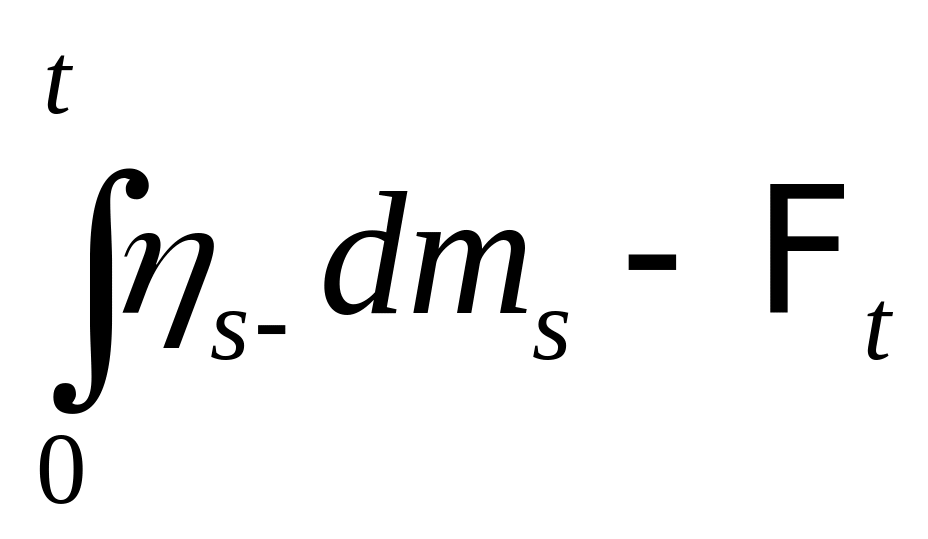- измерим.

Теорема 100. Пусть - ограниченный предсказуемый процесс, а - - мартингал имеющий ограниченную интегрируемую вариацию, т. е. МVar . Тогда определён интеграла Римана - Стилтьеса , являющийся: а) при каждом t - измеримой случайной величиной; б) мартингалом относительно потока и меры Р.

Доказательство. Утверждение а) теоремы очевидно. Установим б). Надо показать, что при 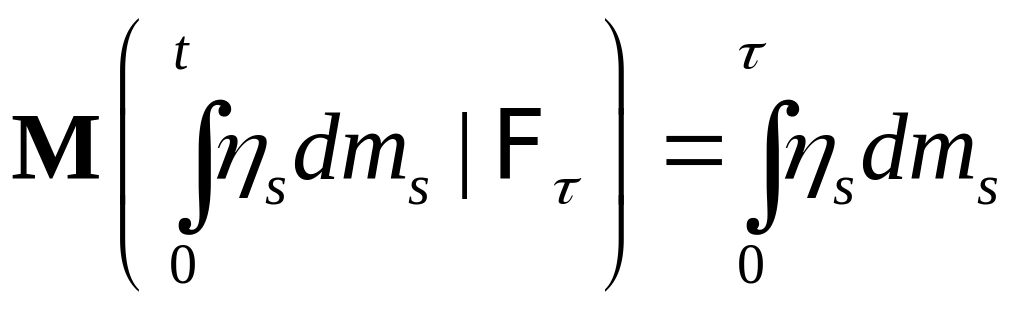P - п. н. Очевидно, что это равенство эквивалентно следующему . Действительно, пусть - разбиение отрезка (, t], тогда имеем .

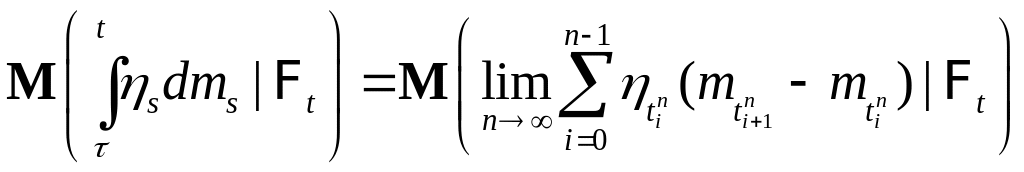По теореме Лебега о можарируемой сходимости, имеем, в силу свойств условного математического ожидания, P - п. н.

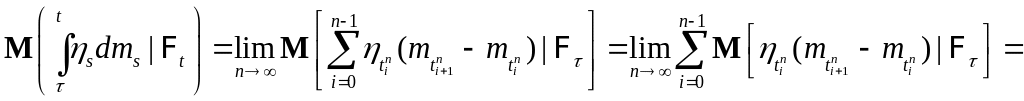
Последнее равенство следует из того факта, что P - п. н. .

Доказательство закончено.

57. Теорема Кэмбелла (следствие 101). Найдите характеристическую функцию Пуассоновского случайного процесса.

Теорема 30 (Кэмбелл). Пусть - считывающий процесс, а его компенсатор относительно меры Р. Пусть - ограниченный предсказуемый процесс. Тогда .

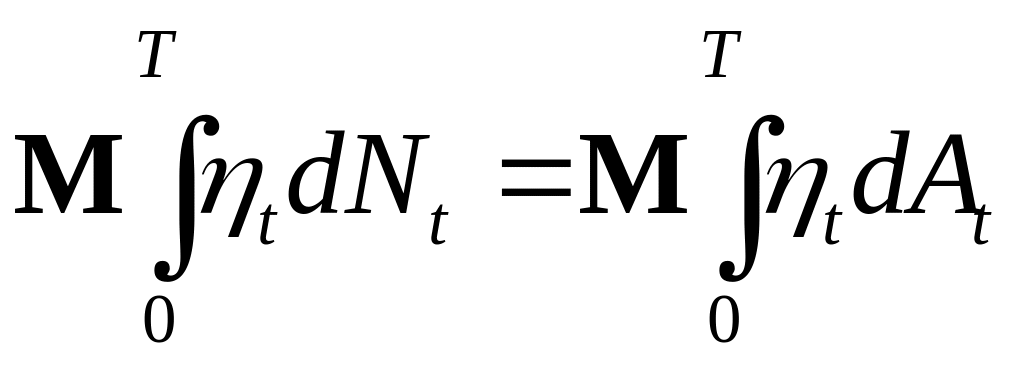Доказательство. Нам надо установить равенство

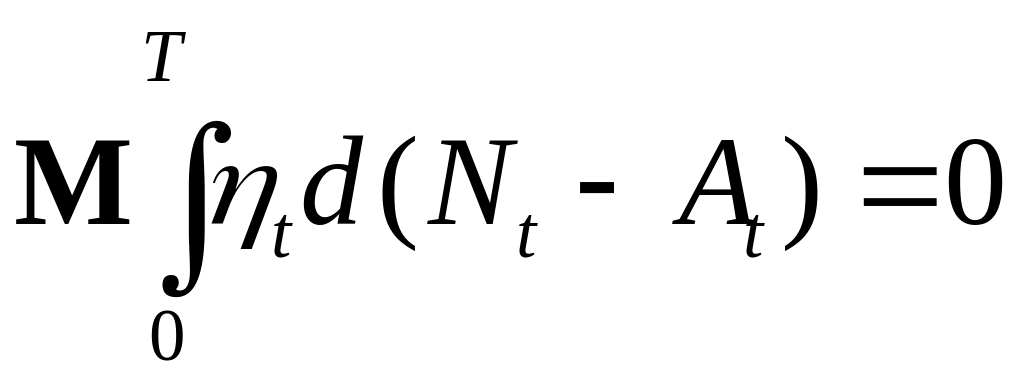(5)

Заметим, что - мартингал, имеющий интегрируемую вариацию, поэтому (5) следует из теоремы 29.

Пример. Пусть пуассоновский процесс с интенсивностью . Найдём его характеристическую функцию. Заметим, сначала, что - мартингал относительно меры P. К функции применим формулу Ито (4), имеем

(6)

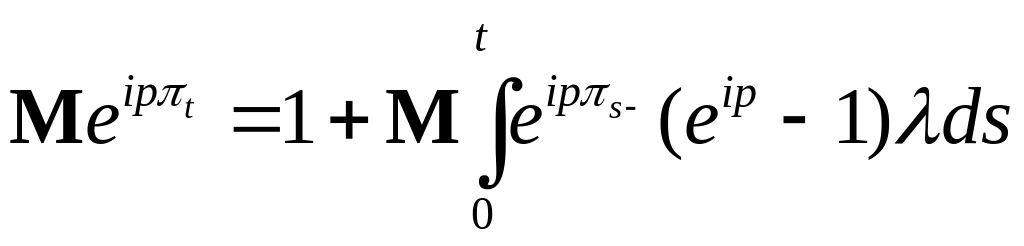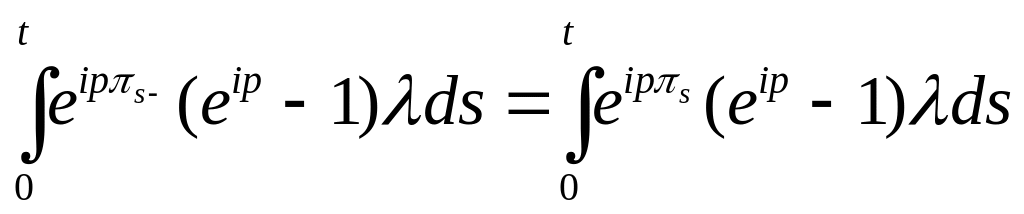Возьмём математическое ожидание относительно левой и правой частей (6), учитывая (5), имеем . Заметим теперь, что . В силу теоремы Фубини имеем: 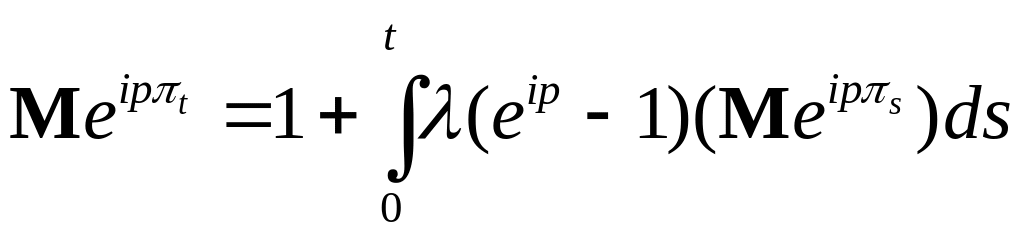. Отсюда следует, что .

58. Свойства компенсатора точечного процесса (теорема 102). Случайная замена времени (теорема 103).

Теорема 102. Справедливы утверждения.

1) Компенсатор точечного процесса допускает един­ственное разложение , где - непрерывная составляющая, - разрывная составляющая.

2) Р - п. н.

3)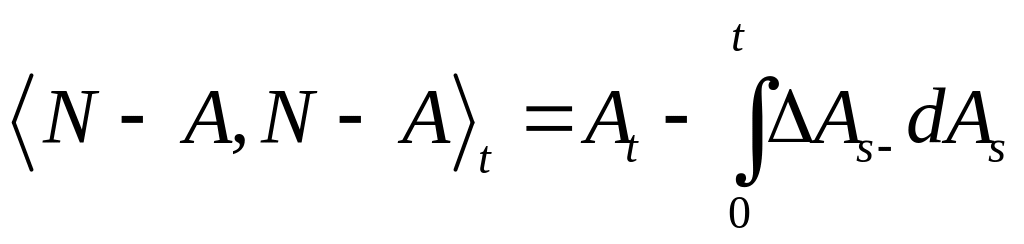 P – п. н. для любого t.

Доказательство. 1) Первое утверждение теоремы следует из теоремы 24.

2) Так как , то . Заметим, что - измерим, поэтому . Так как , то Р - п. н.

3) Сначала заметим, что Р – п. н.

.

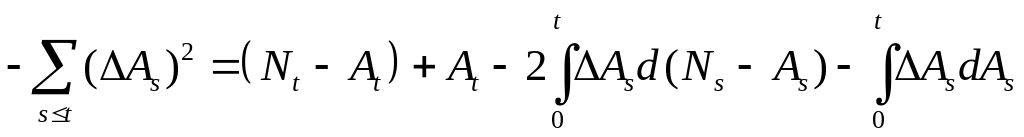Так как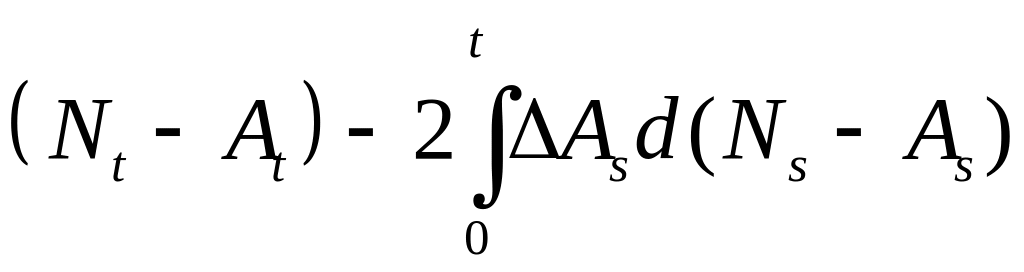 является мартингалом, a 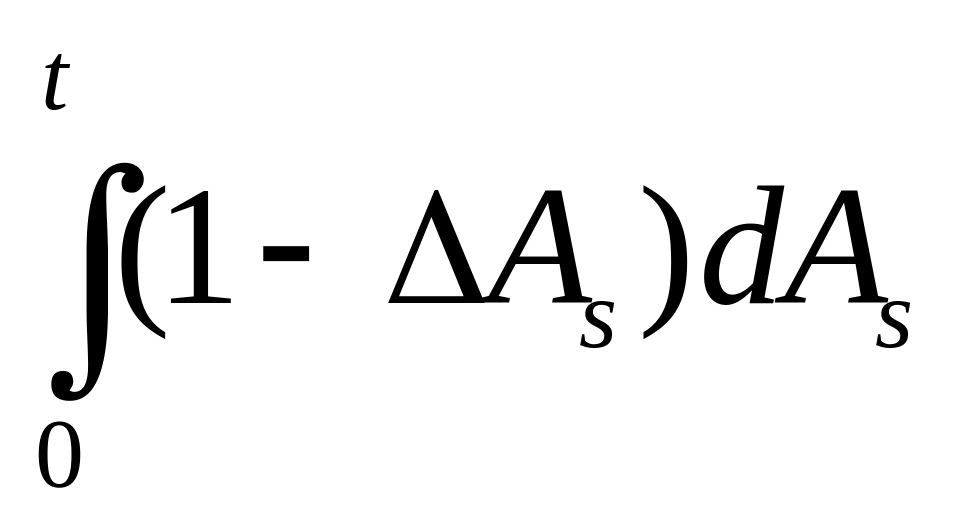- предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана.

8.2. Пусть - точечный процесс, а 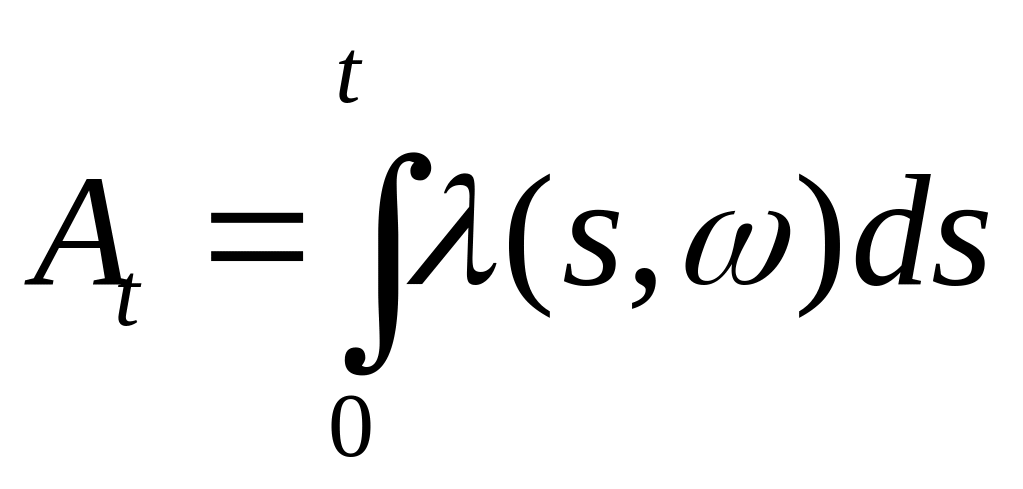- его компенсатор, где - измеримая функция.

Теорема 103. Пусть Р - п. н. 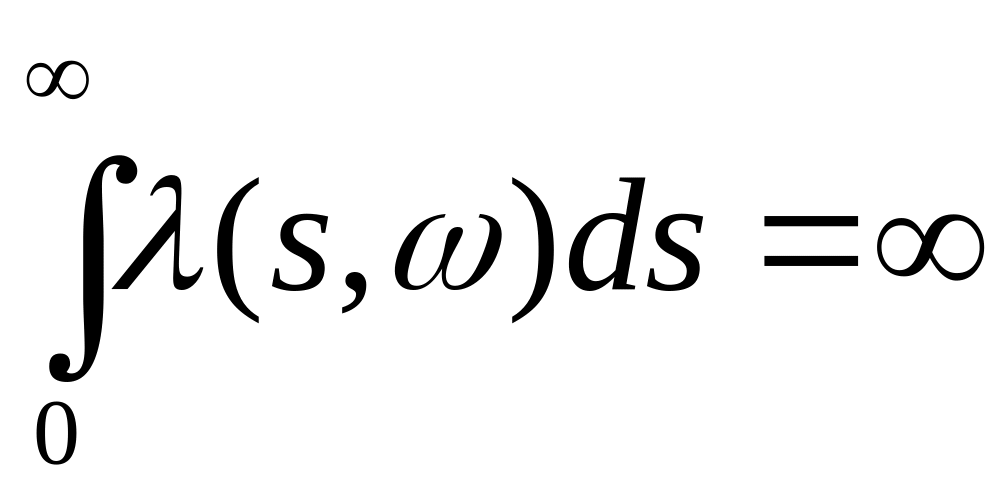. Пусть существует функция

, обозначаемая через , такая, что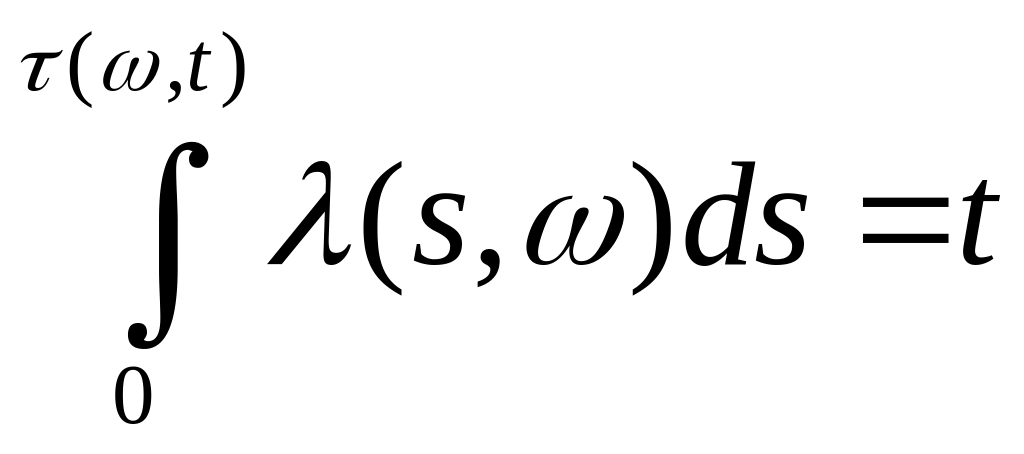 . Тогда - стандартный пуассоновский процесс (т. е. интенсивность его равна единице).

Доказательство. Сначала покажем, что процесс имеет компенсатор t, т. е. - мартингал относительно потока и меры Р. Пусть - ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30, .

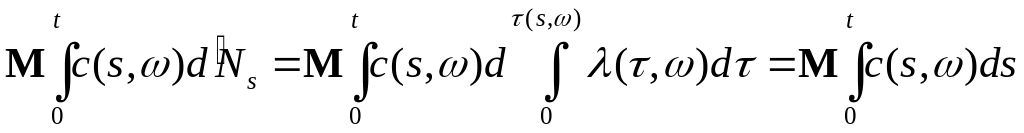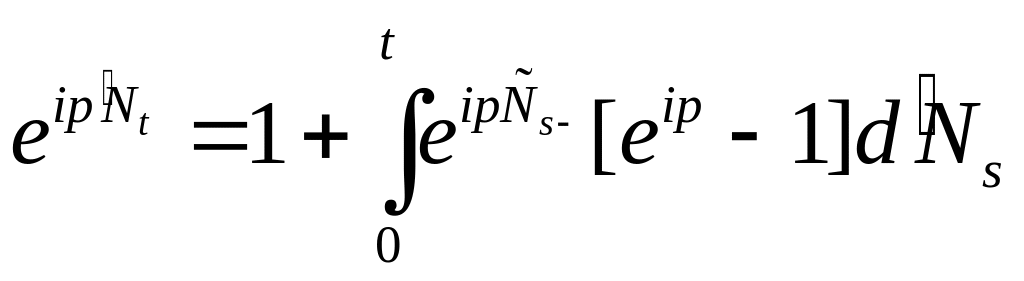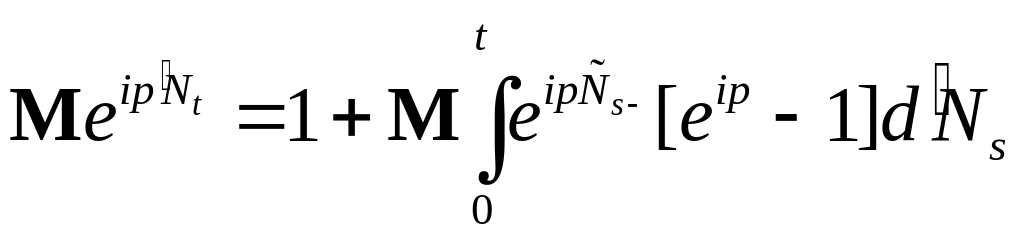Покажем теперь, что . Очевидно, что - точечный процесс, поэтому . Отсюда следует, что . Значит . Доказательство закончено.