38. Однородная Марковская цепь. Классификация состояний однородной марковской цепи (теоремы 69-72)

Пусть на стохастическом базисе задана марковская случайная последовательность со значениями в и переходной вероятностью .

Определение. Пусть Е - не более чем счетное множество (т. е. либо конечное, либо счетное), тогда марковская последовательность называется марковской цепью.

Обозначим через - одноточечное множество. Пусть B любое подмножество множества Е. Очевидно, что . Пусть - переходная вероятность. Очевидно, что .

Обозначим - вероятность перехода последовательностью из состояния в момент времени s в одноточечное множество в момент времени .

Определение. Марковская цепь называется однородной, если , т. е. переходная вероятность зависит только от разности . Если , то - переходная вероятность за один шаг, которую мы будем обозначать через для однородных марковский цепей.

Везде ниже будем рассматривать только однородные марковские цепи.

Займемся теперь классификацией состояний.

Определение. Состояние достижимо из состояния за n шагов (обозначаем ), если .

Теорема 69. Если состояние достижимо из , a достижимо из , то достижимо из .

Доказательство. Так как , то и , то , то в силу соотношения Чепмена - Колмогорова, имеем . Доказательство закончено.

Определение. Состояния и называются сообщающимися, если и (обозначается ).

Очевидно, что: 1) ; 2) если , то ; 3) если и , то .

Определение. Говорят, что состояния и принадлежат классу , если существуют моменты времени и такие, что .

Замечание. Класс - это множество состояний марковской цепи, являющихся сообщающимися. Через обозначим класс состояний, которые сообщаются с состоянием .

Теорема 70. Пусть два класса и , причем и . Тогда .

Доказательство теоремы 70. Пусть , следовательно существуют , такие, что . Из соотношения Чепмена - Колмогорова следует . Аналогично , следовательно . Поэтому . Аналогично устанавливается . Следовательно . Доказательство закончено.

Замечания. 1) Теорема 70 полезна тем, что позволяет разбивать множество состояний на классы , причем .

2) Если - счетно, то классов не более, чем счетно.

Определение. Состояние называется существенным, если для .

Определение. Однородная марковская цепь называется неприводимой, если она состоит из одного класса сообщающихся состояний.

Определение. Состояние называется несущественным, если "выйдя" из него нельзя "вернутся" в него с положительной вероятностью за конечное число шагов.

Из этих определений очевидным образом следуют утверждения.

Теорема 71. Пусть - существенное состояние, тогда из него достижимы все существенные состояния.

Теорема 72. Класс сообщающихся состояний состоит либо из существенных, либо из несущественных состояний.

Определение. Состояние называется циклическим, а называется периодом марковской цепи если:

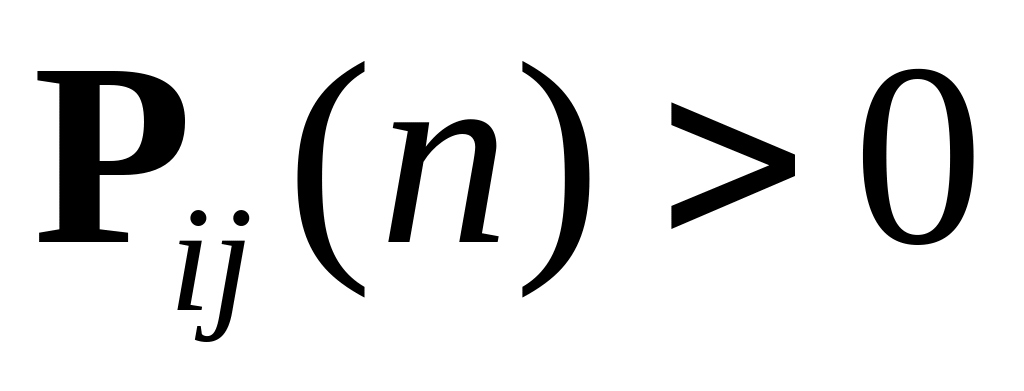1. , где 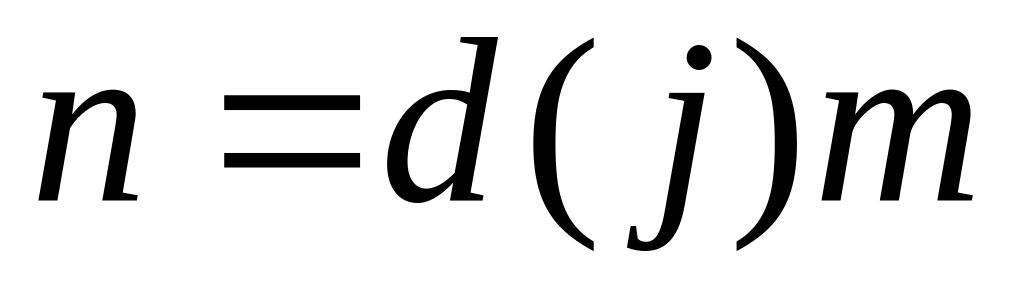( кратно , а );

2. - наибольшее число, на которое делится (НОД - наибольший общий делитель).

Если - НОД, то ясно, что - период марковской цепи. Если , то такая марковская цепь называется апериодической.

Пусть - фиксированное состояние. Введем подклассы:

……………………………………………

Теорема 73. Если марковская цепь - неприводимая, то

!!!!!!!!!!!!!!!!

39. Эргодические цепи маркова. Достаточное условие существование эргодической цепи маркова (теорема 74).

Определение. Однородная марковская последовательность называется эргодической, если существует предел , который не зависит от состояния и выполняются условия:

1) , 2)

Замечание. Эргодические процессы, в отличие от обычных марковских процессов, "не помнят" точку старта.

Теорема 74 (достаточные условия существования эргодического распределения). Пусть - переходная вероятность за один шаг. Пусть существует такое, что . Тогда существует вектор , компоненты которого и , причем для

Доказательство. Из соотношения Чепмена-Колмогорова, имеем

.

Обозначим: Покажем, что при . Действительно ,т. е. .

Аналогично устанавливается неравенство .

Из соотношения Чепмена - Колмогорова следует, что

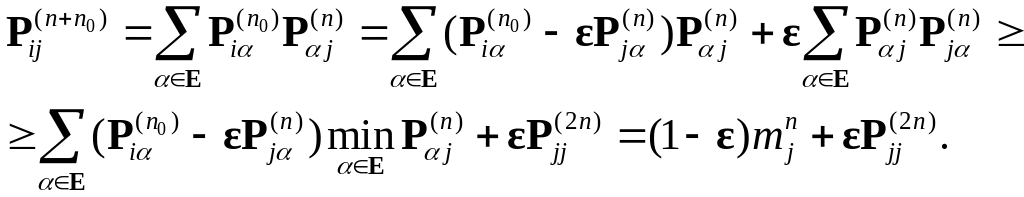
Таким образом для и , имеем отсюда следует неравенство

. (27)

Аналогичным образом легко показать

(28)

Вычтем из (27) (28), имеем . Выбирая кратное (например ), получаем, что . Отсюда следует при . Доказательство закончено.