4. Теорема смещения. Критерии качества оптической системы с произвольным числом Френеля

Оценка качества оптического изображения, формируемого микроволновой или лазерной системой, является одной из важных задач, которую приходится решать в процессе ее расчета, т.е. на стадии моделирования, а также при выходном контроле, т.е. на финишной стадии ее изготовления. Специфика данных систем заключается в жестких требованиях, предъявляемых Заказчиком к их оптическому качеству. В этих условиях, размер пятна рассеяния в плоскости изображения соизмерим с размером дифракционного пятна, т.е. остаточные аберрации оптической системы должны быть предельно малыми. Для определения влияния на качество изображения фазовых искажений, вносимых оптической системой, логично использовать дифракционную теорию аберраций [8], как это было сделано в предыдущем разделе. Важным моментом этой теории является установление допустимых значений остаточных волновых аберраций, а также других критериальных оценок качества.

Первый критерий качества оптической системы, сформулированный с точки зрения физической оптики, был введен Рэлеем: «…аберрация является несущественной, когда она нигде (или, по крайней мере, на относительно небольшой площади) не превышает небольшой доли длины волны. Таким образом, при оценке интенсивности в фокальной точке, где в отсутствие аберрации все вторичные волны имели бы в точности одинаковые фазы, видно, что аберрация, нигде не превышающая /4, может оказать лишь незначительное действие…Основным выводом является то, что аберрация между центром и окружностью в четверть периода оказывает лишь незначительное действие на интенсивность в центральной точке изображения». В течение длительного времени волновой критерий Рэлея считался абсолютно справедливым и не подвергался сомнению. Дальнейшие исследования [38] показали, что его соблюдение не всегда гарантирует получение практически идеальной системы (с числом Штреля Е ≥ 0.8 и хорошей частотно-контрастной характеристикой). Определяющим фактором является характер отклонения формы волновой поверхности от идеальной. Так например, быстро осциллирующая знакопеременная аберрационная функция с максимальным значением не превышающим четверти длины волны не обеспечивает распределения энергии в дифракционном пятне близкого к идеальному. Более точным является критерий Марешаля, который показал, что освещенность в центре дифракционного пятна будет не менее 0.8 от освещенности в идеальной системе, если среднеквадратичное отклонение волнового фронта от опорной сферы, центр которой находится в фокусе, не превышает /14. При монотонно изменяющейся функции аберраций, например, при дефокусировке или сферической аберрации третьего порядка, критерий Марешаля совпадает с критерием Рэлея. Проблема влияния остаточных аберраций на вид дифракционного распределения в фокальном объеме оптических систем с большим числом Френеля достаточно полно освещена в литературе, например [38, 41]. Целью данного раздела явлется уточнение известных результатов дифракционной теории аберраций [8] применительно к анализу систем с малыми числами Френеля.

Для простоты будем считать, что амплитуда поля на зрачке постоянна, т.е. А()=А =const, что соответствует случаю дифракции однородной сходящейся сферической волны, и выражение (2.65) имеет вид (2.96),

(2.96)

Используя оптические переменные u и v вида (2.10), можно определить интенсивность в произвольной точке Q в окрестности параксиального фокуса как

. (2.97)

Интенсивность в параксиальном фокусе (u = v = 0) безаберрационной системы I определена (2.15). Выше было показано, что в идеальной оптической системе (Ф0) с малым числом Френеля максимум интенсивности в изображении точечного монохроматического источника не совпадает с параксиальным фокусом и смещен в направлении выходного зрачка оптической системы в точку с координатой u , которую можно назвать дифракционным фокусом (ДФ). С другой стороны, известно [38], что остаточные аберрации системы приводят к аналогичному эффекту, т.е. смещению максимума интенсивности в любом направлении, определяя положение плоскости наилучшей установки. Согласно терминологии, использованной в [8], максимум интенсивности находится в точке, которую также определяют, как дифракционный фокус. В рассматриваемой ситуации, логичнее было бы определить ее, как аберрационно-дифракционный фокус (АДФ).

Одним из часто используемых числовых параметров, характеризующих качество оптического изображения является число Штреля, под которым понимают отношение максимальной интенсивности в АДФ к интенсивности в параксиальном фокусе идеальной системы (Ф0).

Строго говоря, такое определение числа Штреля справедливо только для систем с большими числами Френеля, т.к. в этом случае максимум интенсивности в дифракционном распределении практически совпадает с параксиальным фокусом. В общем случае логичнее определять число Штреля, как отношение интенсивностей в АДФ и ДФ:

(2.98)

где - координаты, определяющие положение АДФ,

- координаты, определяющие положение ДФ.

Полученное выражение (2.98) не противоречит известному определению и совпадает с ним при больших числах Френеля N.

В дифракционной теории аберраций существует ряд полезных соотношений, позволяющих существенно упростить анализ оптических систем, которые были получены без учета возможной малости числа Френеля. Одним из примеров может служить теорема смещения, играющая важную роль в вычислительной оптике, а также в теории оптических измерений, в частности, при обработке результатов интерференционного контроля объективов. Для центрированной оптической системы, имеющей деформацию волнового фронта в области выходного зрачка, ее формулировка имеет следующий вид:

«Добавление к функции аберраций члена , где H, K, L, M – постоянные порядка , не изменяет трехмерного распределения интенсивности света вблизи фокуса, а только смещает его как целое в соответствии с преобразованиями »

(2.99)

Покажем, что в общем случае, и, в частности, в оптических системах с малым числом Френеля N, указанное изменение аберрационной функции приводит к проективному преобразованию системы координат, которое не является аффинным, т.е. к деформации распределения поля в фокальном объеме.

В соответствии с теоремой, допустим, что две функции аберраций Ф и Ф связаны соотношением , а соответствующие нормированные на интенсивности и определяются выражением, которое можно написать в виде:

, (2.100)

где . Очевидно, можно записать

(2.101)

где , а

из чего следует

. (2.102)

Учитывая уравнения связи (2.6) и (2.10), получим после необходимых преобразований

(2.103)

Полученное преобразование координат можно записать и так:

(2.104)

В предельном случае больших N, что характерно для изображающих оптических систем видимого диапазона, дифракционное поле локализуется в малом фокальном объеме и, соответственно, z и z много меньше радиуса опорной сферы сравнения R. В этом случае выражения (2.104) приводятся к известному виду (2.99).

Связь между нормированными интенсивностями при переходе от функции аберраций Ф к Ф определяется следующим образом:

(2.105)

Полученные результаты позволяют сформулировать теорему смещения в несколько иной форме:

Добавление к функции аберраций члена , где H, K, L, M – постоянные порядка , приводит к смещению трехмерного распределения интенсивности в фокальном объеме оптической системы, сопровождаемому объемной и амплитудной деформациями в соответствии с преобразованиями (2.104) и (2.105).

Изменение функции аберраций, как это обычно используют, можно связать с изменением опорной сферы сравнения. Допустим, что Ф – функция аберраций, связанная с опорной сферой Гаусса, имеющей радиус R и центр кривизны в точке параксиального фокуса Р (Рис. 2.55). Центр новой опорной сферы сравнения выберем в точке Q(x,y,z), лежащей в окрестности параксиального изображения, а радиус положим равным R.

Рис. 2.55. Изменение опорной сферы Гаусса [8]

Очевидно, функция аберраций, отнесенная к новой опорной сфере, имеет вид [8]

, где G – точка пересечения линии NQ c опорной сферой Гаусса, причем NG=NQ - GQ= R - , а определяется выражением (2.8), в которое необходимо подставить значения координат точки Q. Новая функция аберраций будет иметь следующий вид:

(2.106)

Из полученного выражения следует, что коэффициенты H, K, L и M, характеризующие изменение опорной сферы, определяются через координаты точки Q следующим образом:

(2.107)

Как и в предыдущих случаях, полученные соотношения при больших числах Френеля приводятся к хорошо известным выражениям [2"].

Еще одно полезное соотношение, устанавливающее связь между интенсивностью в центре опорной сферы и среднеквадратичной деформацией волнового фронта, требует уточнения в связи с оценкой качества микроволновых изображающих систем. В дифракционной теории аберраций аналогичное соотношение было использовано А. Марешалем [38] при выводе волнового критерия качества оптической системы. Используем известную методику решения данной задачи [8] и попробуем получить более общее аналитическое выражение.

Относительная интенсивность в произвольной точке Q, лежащей в окрестности параксиального изображения, определяется ранее приведенным выражением (2.100). При этом аберрационная функция определена относительно опорной сферы Гаусса, центр которой расположен в начале выбранной системы координат, а радиус равен R. Предположим, что Ф - аберрационная функция, отнесенная к новой опорной сфере с центром в точке Q. Согласно (2.100) и (2.103) можно записать:

. (2.108)

Учитывая малость остаточных аберраций, можно разложить подынтегральную функцию в ряд, ограничившись членами второй степени, т.е. . По определению, среднее значение n – ой степени Ф равно:

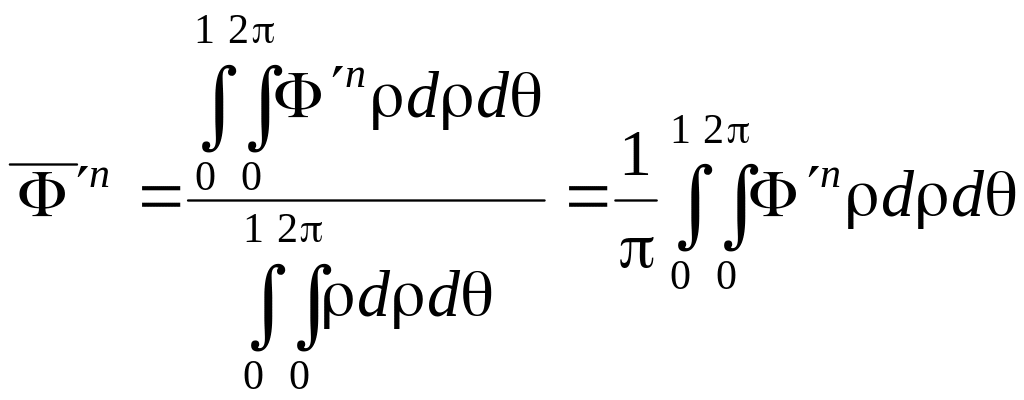
и относительная интенсивность в точке Q определяется выражением

. (2.109)

Величина в квадратных скобках представляет собой среднеквадратичную деформацию волнового фронта (Ф)

,

и, окончательно, искомое соотношение имеет вид:

. (2.110)

В оптических системах с большим N (z много меньше R) сомножитель перед квадратными скобками практически не отличается от единицы и (2.110) совпадает с ранее известным выражением. Полученный результат позволяет сделать вывод, что интенсивность в центре опорной сферы сравнения вблизи параксиального фокуса не зависит от природы аберраций, а определяется только среднеквадратичной деформацией волнового фронта. В отличие от ранее известного, ее отклонение от единицы будет определяться не только величиной (Ф) , но и величиной сомножителя , присутствие которого в формуле физически оправдано деформацией фокального распределения относительно плоскости Гаусса и смещением модального значения в сторону выходного зрачка оптической системы.

Ранее было показано, что одной из характерных особенностей дифракционного поля в фокальном объеме оптических систем с малым числом Френеля является смещение главного максимума вдоль оптической оси в направлении выходного зрачка и нарушение симметрии распределения относительно плоскости Гаусса. Таким образом, точка геометрического фокуса перестает быть характерной точкой аксиального распределения интенсивности, и определение ее положения в процессе измерений становится проблематичным. Логичным выходом из этой ситуации является перенос центра опорной сферы сравнения, а также начала системы координат, из точки геометрического фокуса в точку максимума аксиального распределения – дифракционный фокус. Фактически это означает введение в систему дефокусировки. Для упрощения рассматриваемой ситуации примем, что дефокусировка является единственной аберрацией системы – Ф  0. Также как и ранее, примем за начало системы координат точку геометрического фокуса, совпадающую с центром опорной сферы Гаусса радиуса R. Центр новой опорной сферы сравнения, имеющей радиус R, расположен в точке Q(x,y,z). Рассматривая случай осевого точечного источника, можно положить x=y=0, а z= (где  - дефокусировка со знаком, определяемым направлением смещения). Из выражения (2.8) следует

(2.111)

и формула принимает вид:

(2.112)

В соответствии с теоремой смещения можно утверждать, что введение дефокусировки  соответствует введению в аберрационную функцию полинома , где H, K, L, M согласно (2.107) имеют следующие значения: . В новой системе координат XYZ, центр которой совпадает с точкой Q, относительная интенсивность может быть записана, как

. (2.113)

При этом безразмерная переменная u в штрихованной системе координат имеет значение:

.

После преобразования окончательное выражение примет вид

(2.114)

и, в частном случае 0, R=R, z=z, совпадает с (2.20).

Проанализируем полученное выражение, чтобы доказать его инвариантность по отношению к дефокусировке. Анализ аналогичен приведенному в разделе 2.1.1 для (2.20).

Дифференцируя (2.114) по z и, приравнивая полученную производную к нулю, найдем корни соответствующего уравнения. В данном случае решение распадается на два возможных варианта:

1. . (2.115)

Тогда координаты минимумов аксиального распределения интенсивности в системе координат XYZ :

. (2.116)

Сравнивая полученную формулу (2.116) с (2.22) отметим, что введение в систему дефокусировки  приводит к смещению с обратным знаком минимумов аксиального распределения вдоль оптической оси.

2. . (2.117)

Полученное уравнение является трансцендентным и аналитически не решается. Его корни определяют координаты максимумов аксиального распределения интенсивности в системе координат XYZ. Воспользовавшись методикой анализа подобного уравнения, описанной в разделе 2.1.1, можно показать, что приближенно ( с точностью не хуже 1%) координату главного максимума аксиального распределения интенсивности можно найти из решения уравнения , причем

. (2.118)

Из (2.118) следует, что в системе координат XYZ максимум главного дифракционного порядка смещен вдоль оптической оси на величину -.

В заключение, можно привести несколько иную, и, возможно более удобную, форму записи аксиального распределения интенсивности в системе координат с произвольно выбранным началом:

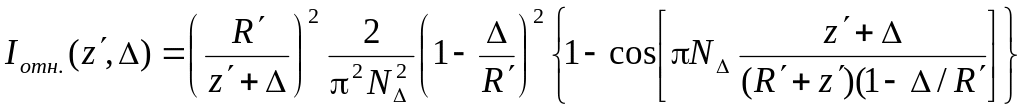, (2.119)

где – число Френеля, связанное с центром выбранной сферы сравнения (с началом системы координат XYZ).