Аксиальное амплитудно-фазовое распределение
Под аксиальным
распределением будем понимать
распределение поля вдоль оптической
оси, т.е. для точек с координатой r=0.
Очевидно, что в этом случае оптическая
переменная v
равна нулю и, соответственно, функции
Ломмеля
Тогда
.
(2.19)
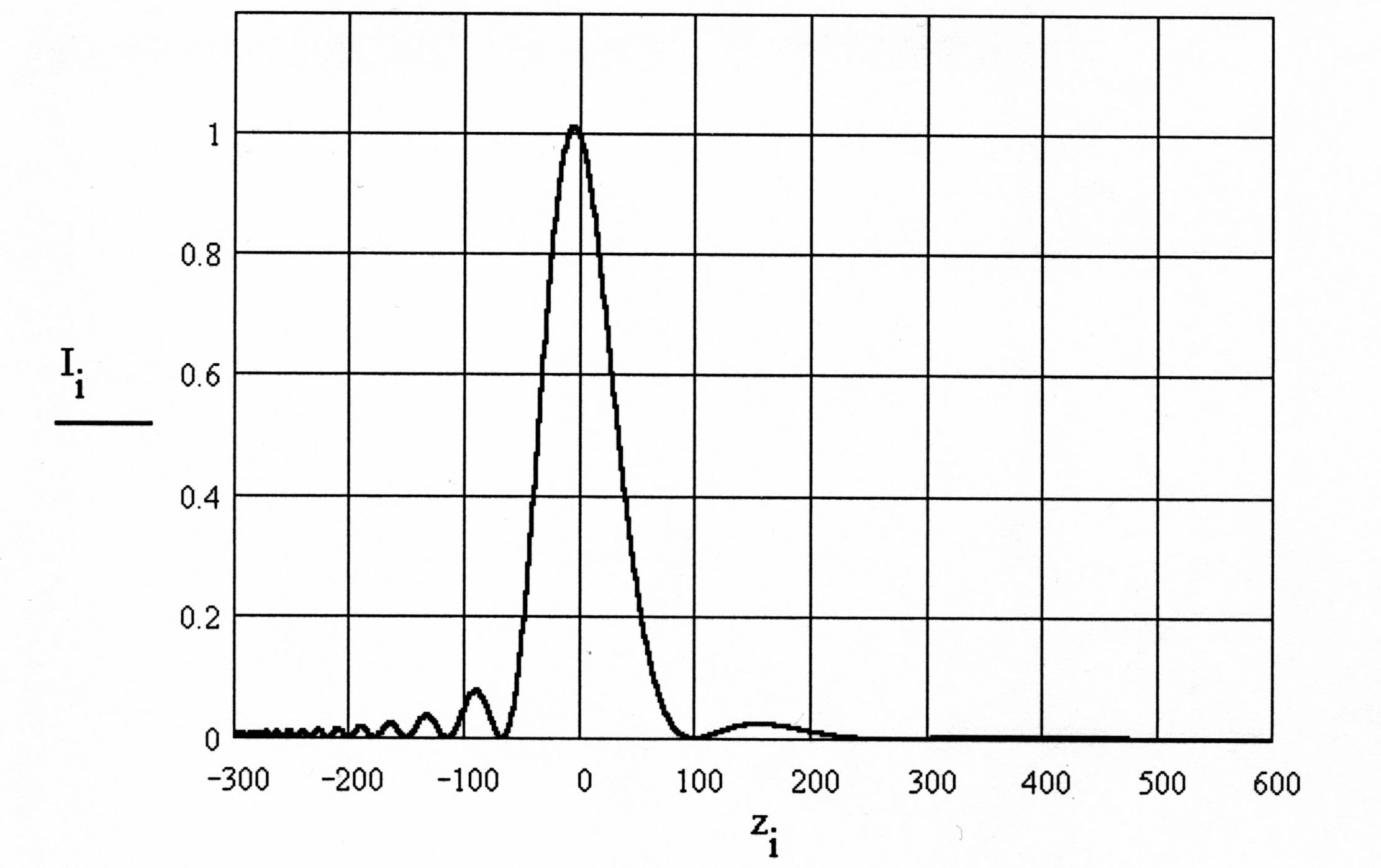
Вид распределения I(z) для нескольких значений N представлен на рис. 2.2.
а (N=3.46) б (N=10) в (N=100)
Рис. 2.2 Аксиальное распределение относительной интенсивности
Представляет интерес определение экстремумов этой функции в исходной цилиндрической системе координат. Для этого необходимо записать выражение (2.19) в виде
(2.20)
и, приравняв к нулю первую производную по z, решить полученное уравнение:
(2.21)
Возможны два случая:
1.
и
,
где n=1,2,3.…
Это условие соответствует минимумам I(z) (n = 0 исключено, так как в этом случае z = 0, что, соответственно, требует наличия экстремума в параксиальном фокусе).
Таким образом, координаты минимумов аксиального распределения относительной интенсивности в области z 0 можно определить по формуле
,
а в области z
0, соответственно,
.
(2.22)
2.
.
Учитывая рассмотренный выше случай,
данное выражение можно преобразовать
к виду:
.
(2.23)
В
этом случае уравнение (2.23) является
трансцендентным и аналитически не
решается. Его корни определяют координаты
максимумов аксиального распределения
интенсивности. Как правило, наибольший
интерес представляет определение
координаты максимума главного
дифракционного порядка. Обозначим
=.
Известно, что на интервале
функцию ctg
можно представить суммой членов
сходящегося ряда:
ctg
=
,
где
– числа Бернулли. Из условия сходимости
следует, что z
z
z
находится в промежутке между первыми
минимумами функции
,
что, естественно, выполняется, так как
нас интересует только координата
максимума главного дифракционного
порядка. Априори известно, что она
заключена в
интервале z
z
0. Приближенное выражение, позволяющее
определить z
c
точностью не хуже 1%, для квазиоптических
систем с числом Френеля не менее 2 имеет
вид:
.
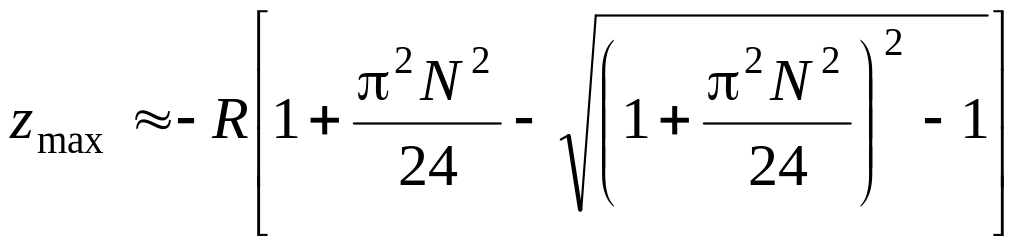(2.24)
Условие минимумов функции позволяет определить линейные размеры осевых дифракционных порядков. Легко показать, что
(2.25)
где L
–
размер главного
(нулевого) дифракционного порядка; L
и
L
– размеры 1-х дифракционных порядков в
области z >
0 и z <
0, соответственно.
Из отношения
следует, что с увеличением числа Френеля
(N
4,
так как в противном случае второй минимум
z
отсутствует,
и говорить о первом положительном
дифракционном порядке бессмысленно)
линейный размер первого положительного
дифракционного порядка стремится сверху
к значению 0.5
,
что характерно для дифракционных
распределений в оптических системах с
большими числами Френеля. В то же время
из
видно, что линейный размер первого
отрицательного дифракционного порядка
стремится снизу к значению 0.5
(в данном случае N
2, так как в противном случае отсутствует
первый минимум z
,
и бессмысленно говорить о линейном
размере главного дифракционного
порядка). Из приведенных результатов
следует, что даже в безаберрационной
системе, характеризующейся малым числом
Френеля, наблюдается значительная
деформация дифракционного поля в
фокальном объеме, а именно:
максимум главного дифракционного порядка смещен по оси z в сторону выходного зрачка системы тем больше, чем меньше число Френеля;
значение интенсивности в главном максимуме больше, чем в параксиальном фокусе. В связи с этим точку z можно назвать дифракционным фокусом оптической системы;
линейные размеры одинаковых по номеру отрицательных и положительных дифракционных порядков не равны друг другу. В отрицательном направлении оси z дифракционное распределение cжато, в положительном – растянуто;
с увеличением числа Френеля характер указанных деформаций уменьшается, и распределение симметрируется относительно плоскости Гаусса.
Рассмотрим особенности поведения аксиального фазового распределения. В этом случае цилиндрическая и безразмерная координаты точки наблюдения Q равны нулю, r=u=0, и интегралы (2.14) имеют вид
,
.
Комплексная амплитуда дифракционного поля может быть записана в цилиндрической системе координат в виде
,
(2.26)
где фазовая функция Ф(z) с точностью до временного члена определяется выражением
,
(2.27)
В монографии [2] аналогичное выражение для фазовой функции выглядит так:
,
(2.28)
Рис. 2.3 Аксиальное распределение фазы при различных числах Френеля (N=0.5, 1.0, 3.46, 10, 100) без учета составляющей kz.
Из (2.27) и (2.28) следует,
что Ф(z)
и Ф
(z)
являются многозначными функциями. В
параксиальном фокусе (z=0)
их главные значения (n=0)
равны
.
В отличие от Ф
(z),
линейно зависящей от координаты z,
поведение фазовой функции Ф(z)
более сложно. Разница определяется
членами
и
.
Легко показать, что разность фаз в двух точках на оси с координатами z и z равна
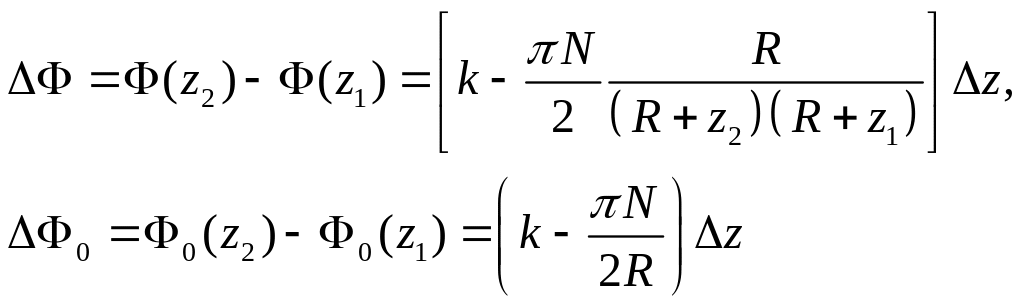(2.29)
где
,
а
– волновое число.
Таким образом
,
а
.
Из этого следует, что в случае
квазиоптической системы фазовое
распределение вдоль оси деформировано,
а именно: в области z
0 – сжато, а в области z
0 – более растянуто. Следовательно,
ранее известное свойство симметрии
в общем случае нарушается, и для систем
с произвольным числом Френеля справедливо
соотношение
.
(2.30)