2.1.2. Амплитудно-фазовое распределение в геометрической фокальной плоскости

Распределение интенсивности в геометрической фокальной плоскости (плоскости Гаусса) легко может быть получено из (2.17) при условии u0 и выглядит следующим образом:

(2.31)

Уравнение представляет хорошо известное распределение Эйри (рис. 2.4). Для систем с малыми числами Френеля, для которых характерно смещение максимума аксиального распределения интенсивности, представляет интерес расчет интенсивности в плоскостях, параллельных плоскости Гаусса, например в плоскости наилучшей установки, проходящей через дифракционный фокус, осевая координата которого определяется выражением (2.23) (рис. 2.5, 2.6).

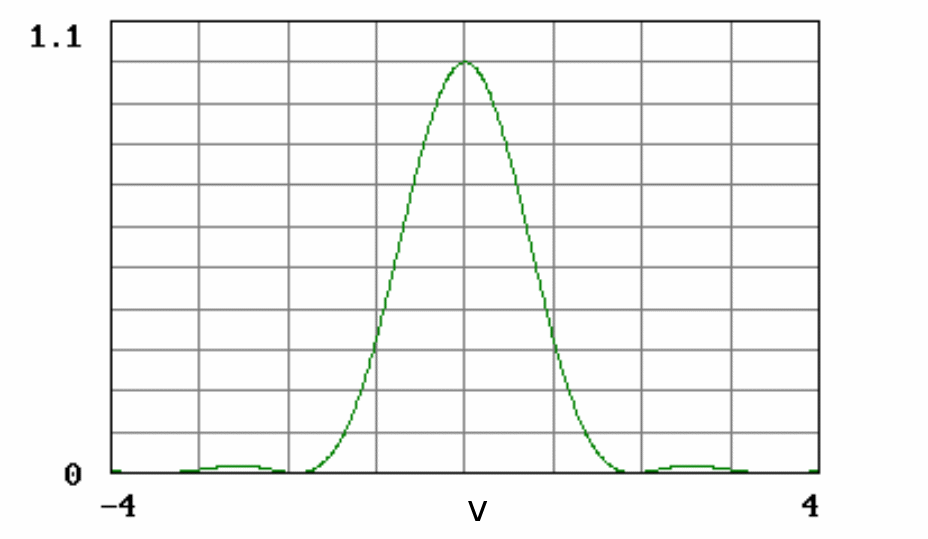
Рис. 2.4. Распределение Эйри

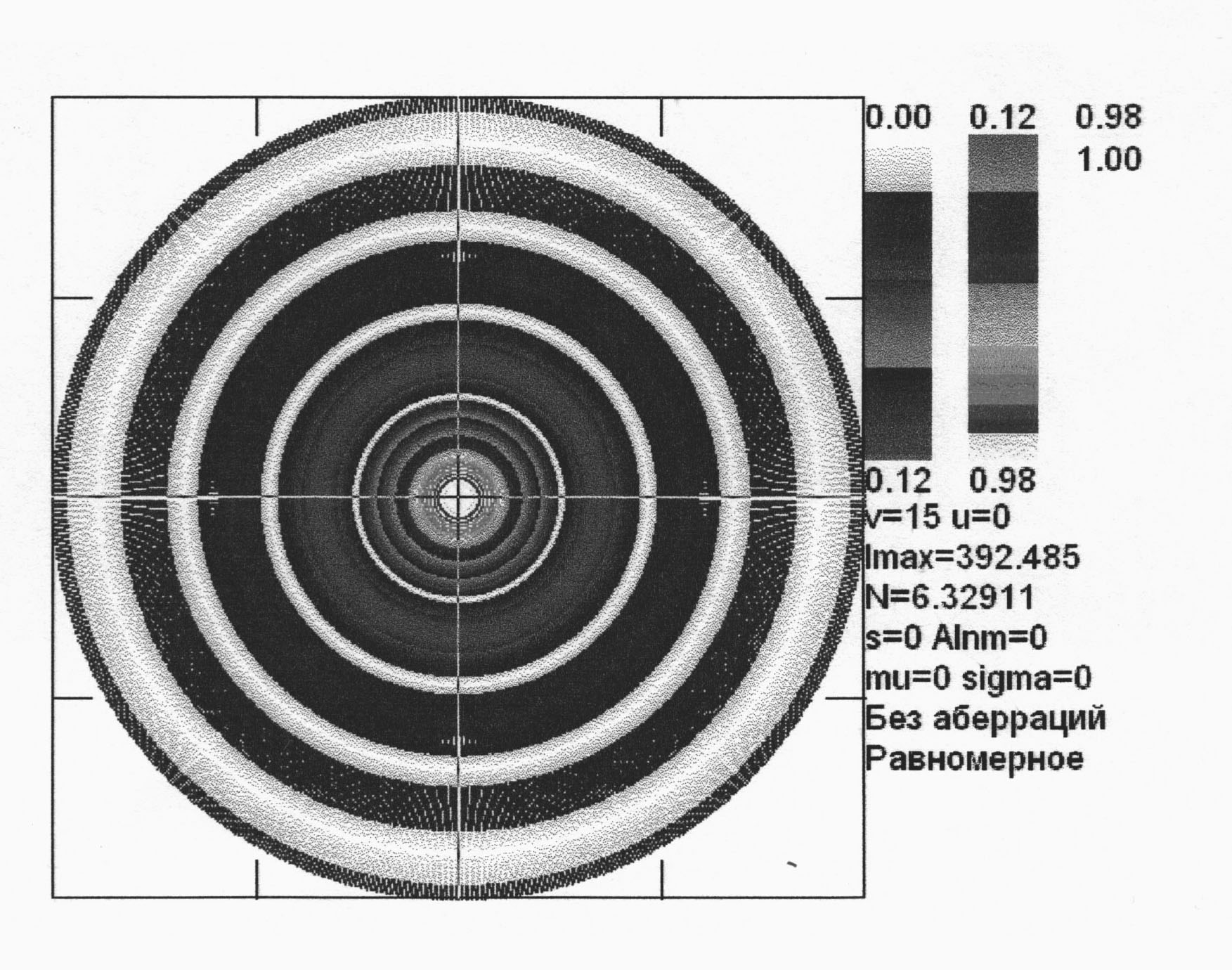
Рис. 2.5 Распределение интенсивности в геометрической фокальной плоскости системы с числом Френеля N = 6.33.

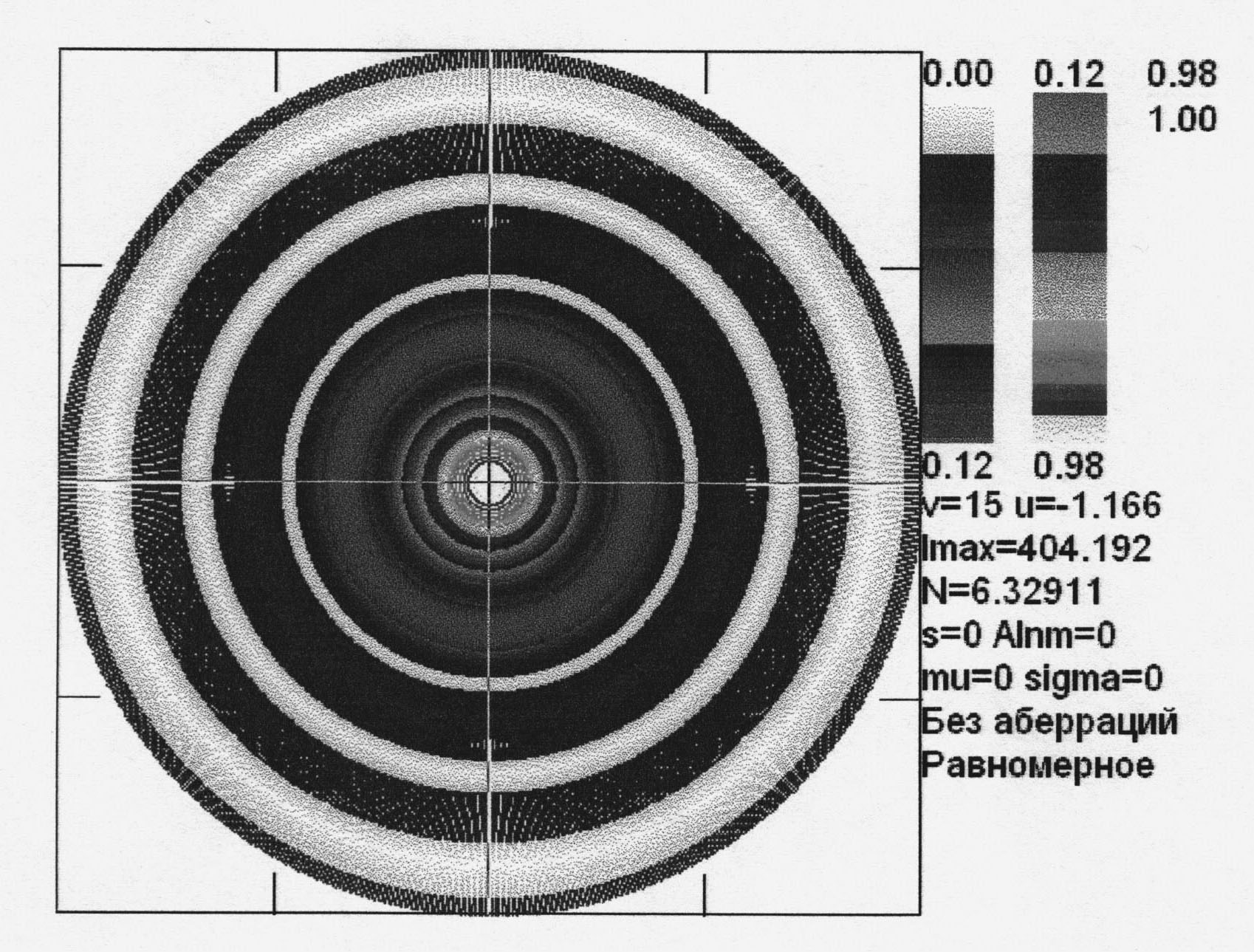
Рис. 2.6. Распределение интенсивности в дифракционном фокусе (N=6.33, u=-1.166)

Анализ фазового распределения можно провести на основе выражения (2.13) для комплексной амплитуды поля в произвольной точке наблюдения Q в окрестности параксиального фокуса. Для этого в качестве фазовой функции возьмем комплексную часть (2.13):

, (2.32)

где

, ,

а интегралы C и S известны по формуле (2.14). Приведенное выражение (2.32) позволяет провести всесторонний анализ поведения волнового фронта дифрагирующей волны в фокальном объеме. При этом стоит заметить, что функция Ф(u,v) является многозначной функцией, с точками ветвления в местах, где интенсивность равна нулю. В этих точках фазовая функция (2.32) не определена. Подробно проблема сингулярных точек фазовой функции рассмотрена в работах Li Y. В точке фокуса (u=0, v=0), не являющейся узловой точкой, определим главное значение фазовой функции как

Ф(0,0)= - .

Для точек наблюдения, расположенных в геометрической фокальной плоскости, оптическая переменная u=0 и, соответственно, выражение для фазовой функции примет вид

. (2.33)

При u = 0  вычисляется через соотношения

, ,

из чего можно сделать вывод, что  = 0 или , в зависимости от знака функции . Тогда формула (2.33) может быть записана как (для случая  = 0) или (для случая  = ).

Графики фазовой функции для систем с числами Френеля 0.5, 1.0, 3.46 и 10 представлены на рис. 2.7.

Как видно из приведенных графиков, в ряде точек вдоль оси v происходит скачкообразное изменение фазы на . В этих точках находятся минимумы интенсивности, определяющие границы колец Эйри. В пределах каждого кольца фаза волны изменяется по параболическому закону.

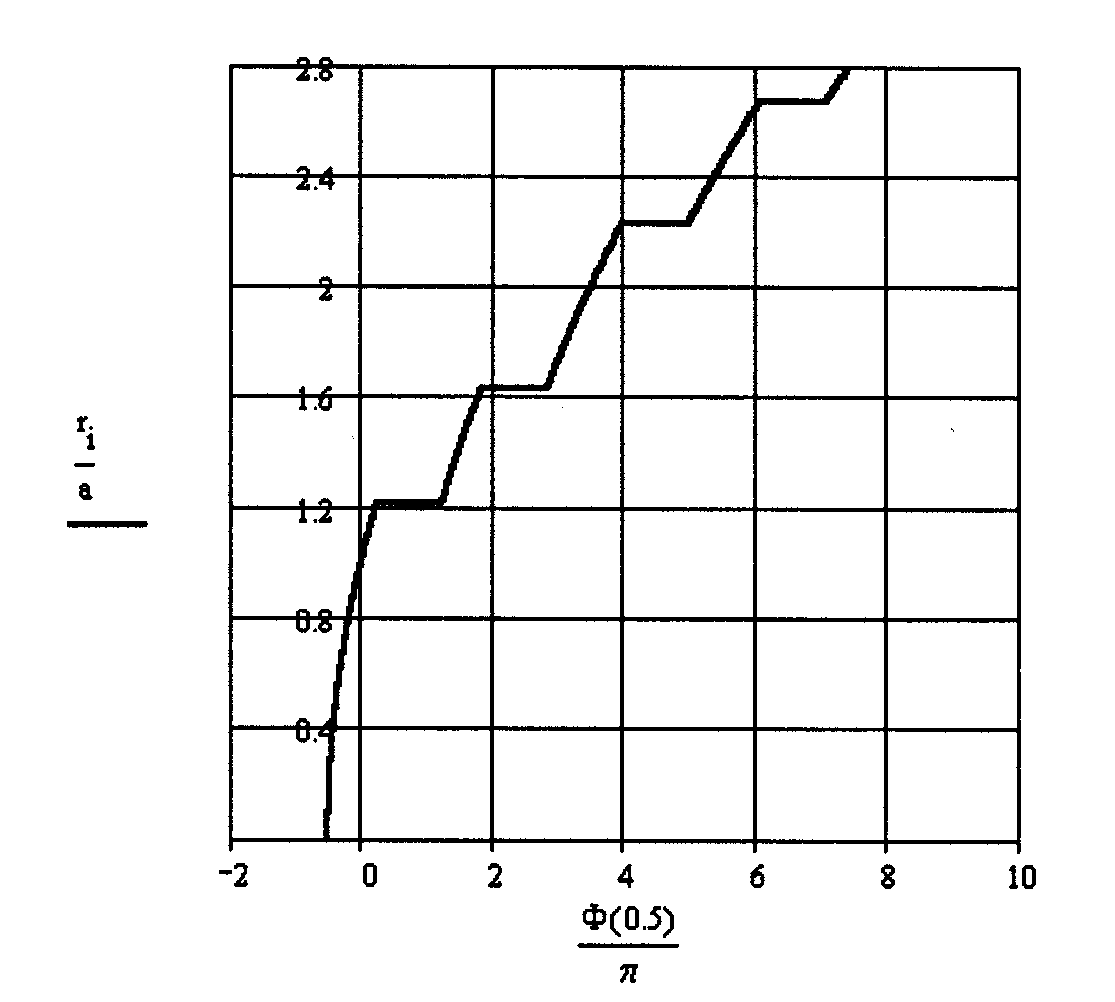
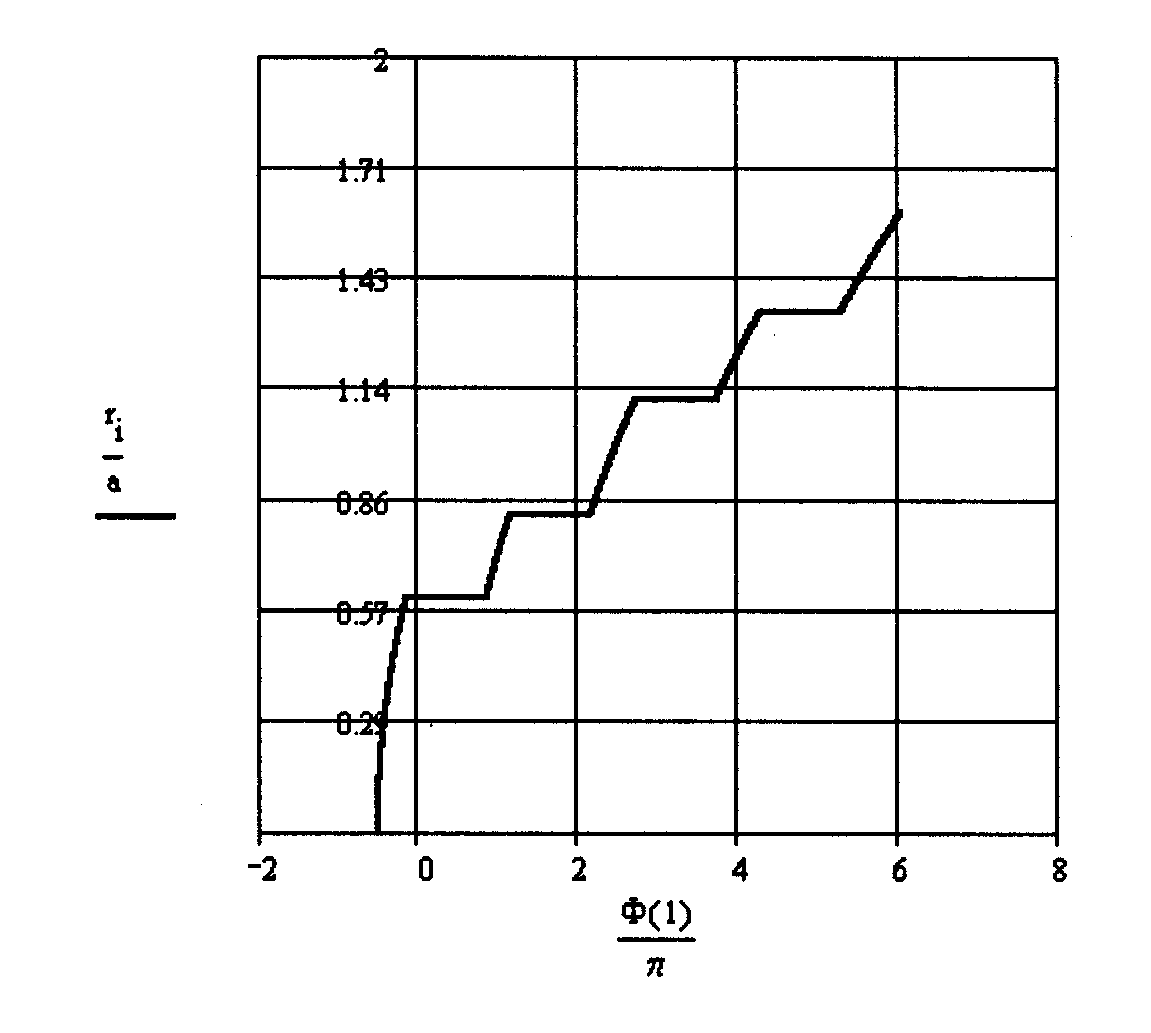
а б

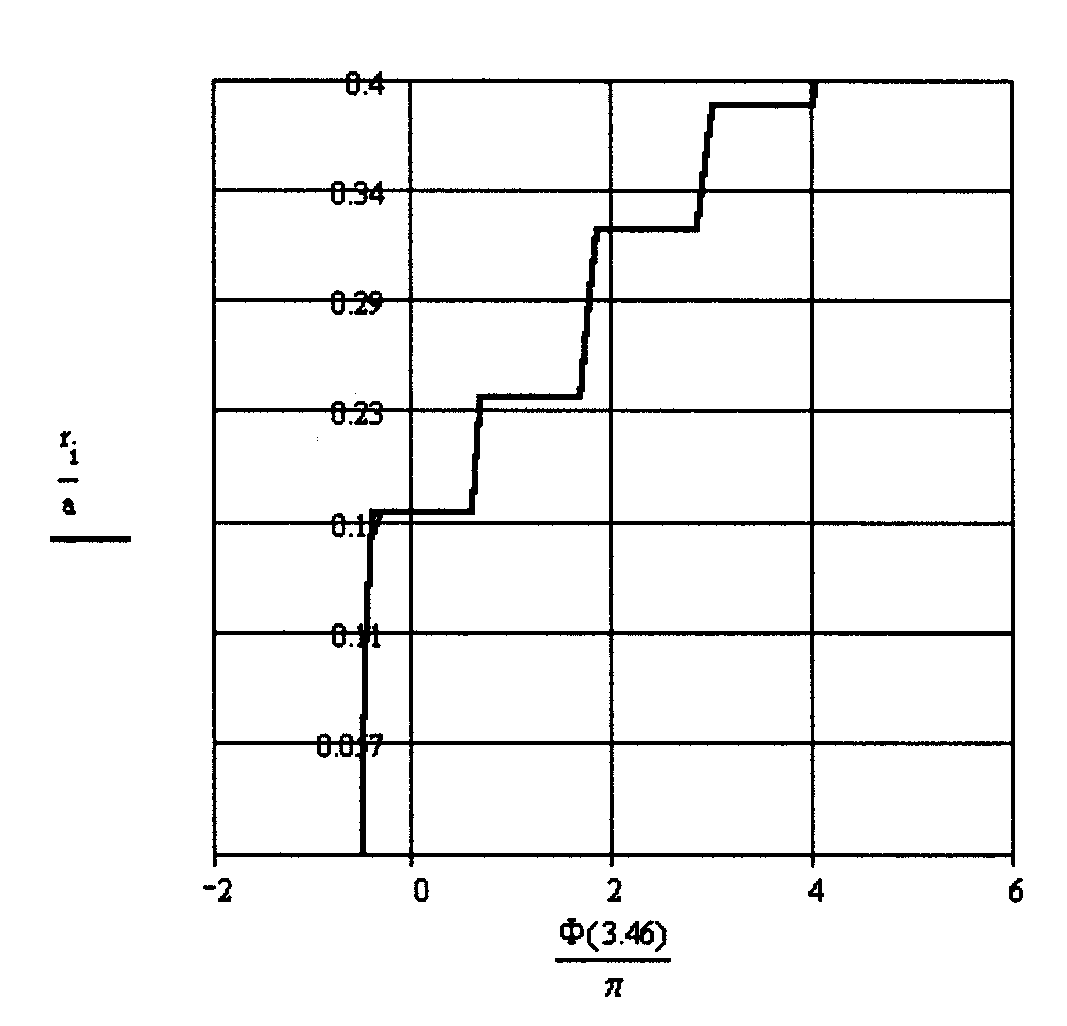
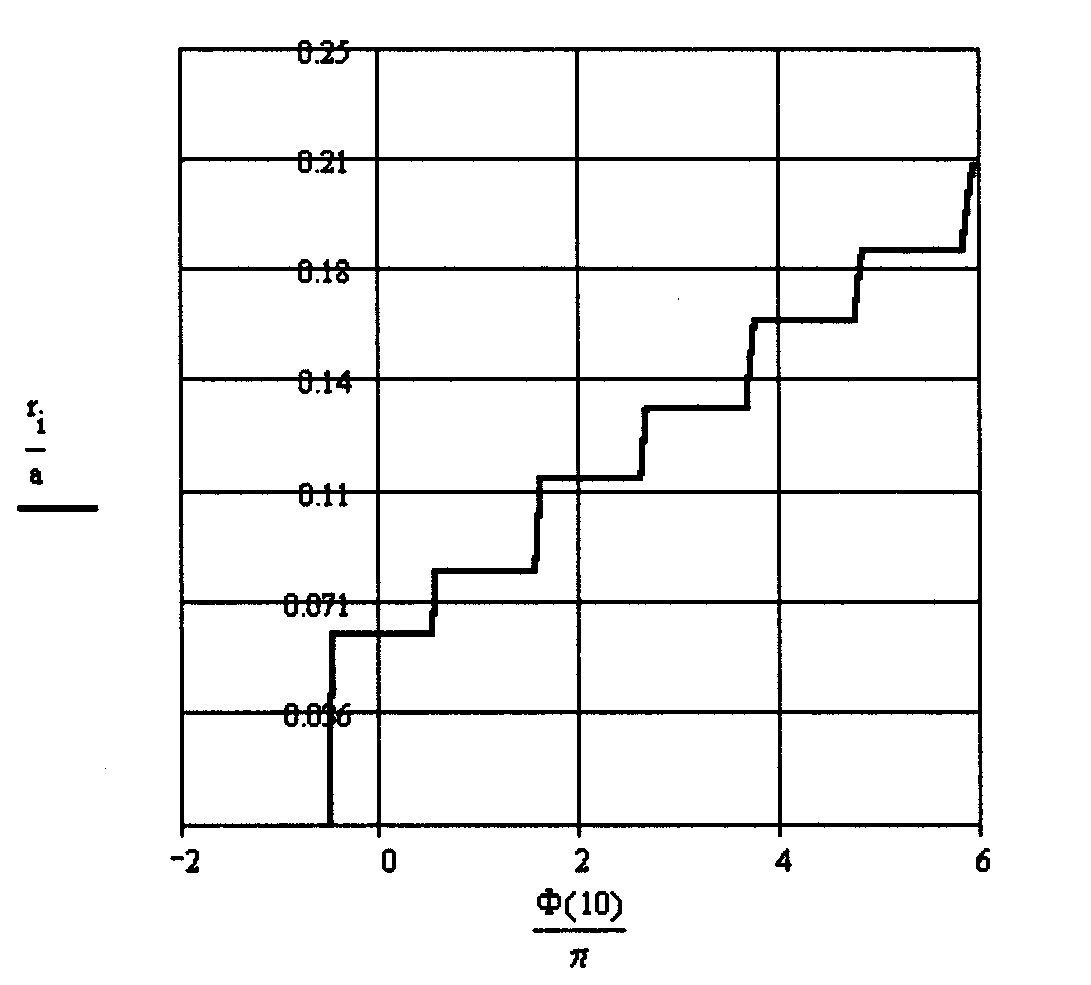
в г

Рис. 2.7. Графики фазовой функции для системы с различными числами Френеля, а - N=0.5, б - N=1.0, в - N=3.46, г - N=10.

2.1.3. Структура поля в меридиональной плоскости оптической системы

Для случая идеальной (без аберрационной) оптической системы с большим числом Френеля структура поля в фокальном объеме достаточно хорошо изучена [2] и обычно представляется в виде изофот, т.е. линий постоянной интенсивности. Характерной особенностью является симметрия картины относительно оптической оси системы (оси z или u) и геометрической фокальной плоскости. Как было показано ранее (см. раздел 2.1.1), в общем случае произвольных чисел Френеля симметрия амплитуды и фазы относительно геометрической фокальной плоскости нарушается по мере уменьшения N. Иллюстрацией этого утверждения служат приведенные на рис. 2.8–2.9 распределения интенсивности в меридиональной плоскости оптических систем с N = 10 и N = 1000. Для расчета были использованы выражения (2.17) и (2.18) а также разработанные программы INTREAL и TVISTOPO. На рис. 2.8 хорошо видно, как дифракционный объем вытягивается вдоль оптической оси, формируется перетяжка в области фокуса и происходит ее смещение в направлении выходного зрачка оптической системы.

Еще одной отличительной особенностью поведения дифракционного поля в фокальном объеме оптической системы при уменьшении числа Френеля является характер фазовых аномалий. В классической теории фокусировки проблеме фазовых аномалий на протяжении ряда лет уделялось внимание многими исследователями [8]. Было обосновано, что однородная сходящаяся сферическая волна испытывает резкий скачок в  при прохождении через фокус.

Исследуем поведение фазы вдоль геометрического луча, идущего под углом к оптической оси и проходящего через фокус. Если  – угол между оптической осью и выбранным геометрическим лучом, то можно записать:

(2.34)

Рис. 2.8. Число Френеля N = 10

Рис. 2.9 Число Френеля N = 1000

Подставляя формулу (2.34) в (2.32), получим:

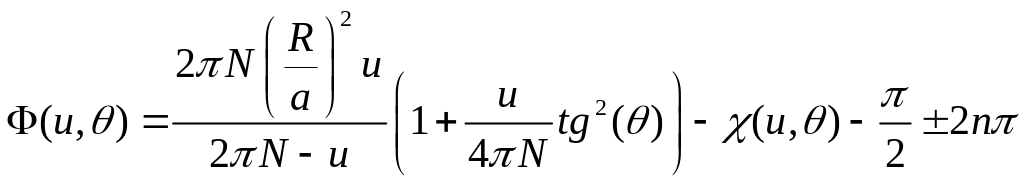. (2.35)

Введем опорную сферическую волну с комплексной амплитудой

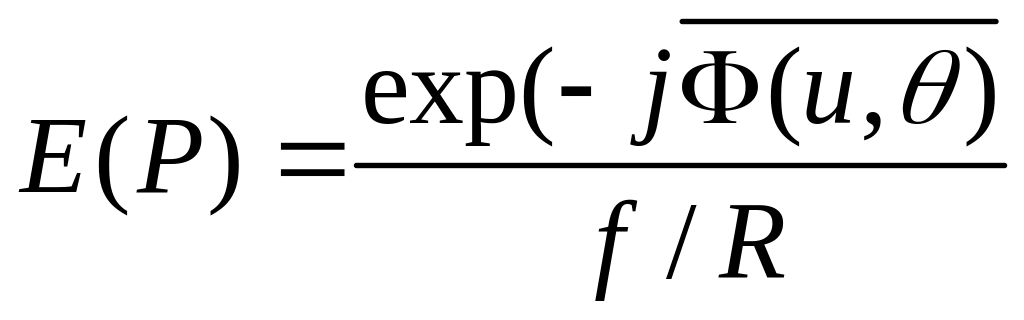, , (2.36)

где 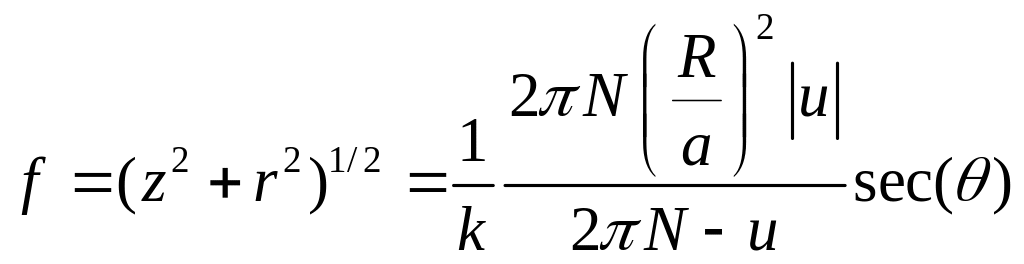– расстояние между точкой наблюдения Q и точкой P (см. рис. 2.1);  = -kf при u0 и  = +kf при u0. Разница между фазами дифрагирующей и опорной волн называется аномалией фазы вдоль геометрического луча [8]:

,

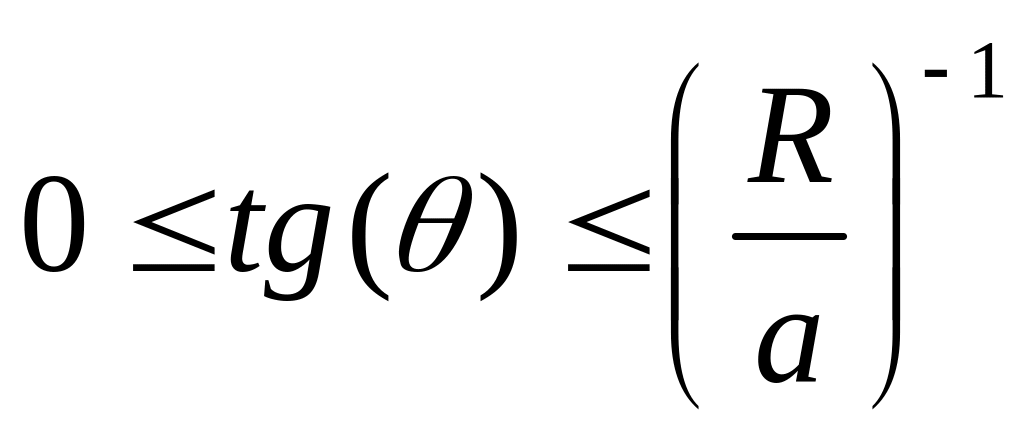. (2.37)

Результаты расчетов по формуле (2.37) приведены на рис. 2.10–2.13. Каждая кривая на рисунке соответствует отдельному геометрическому лучу, начиная с угла  = 87.8 (граница геометрической тени), для углов  = 6, 4, 2, 30 и луча, лежащего на оптической оси. Для всех графиков параметр R/a = 7.

Из графиков видно, что характер деформаций волнового фронта относительно опорной сферы по одним и тем же лучам в области z  0 и z  0 одинаков для систем с большими N и различен в случае малых N. И в одном, и в другом случаях деформации фрагментов волнового фронта, соответствующих лучам, идущим под разными углами, различны.

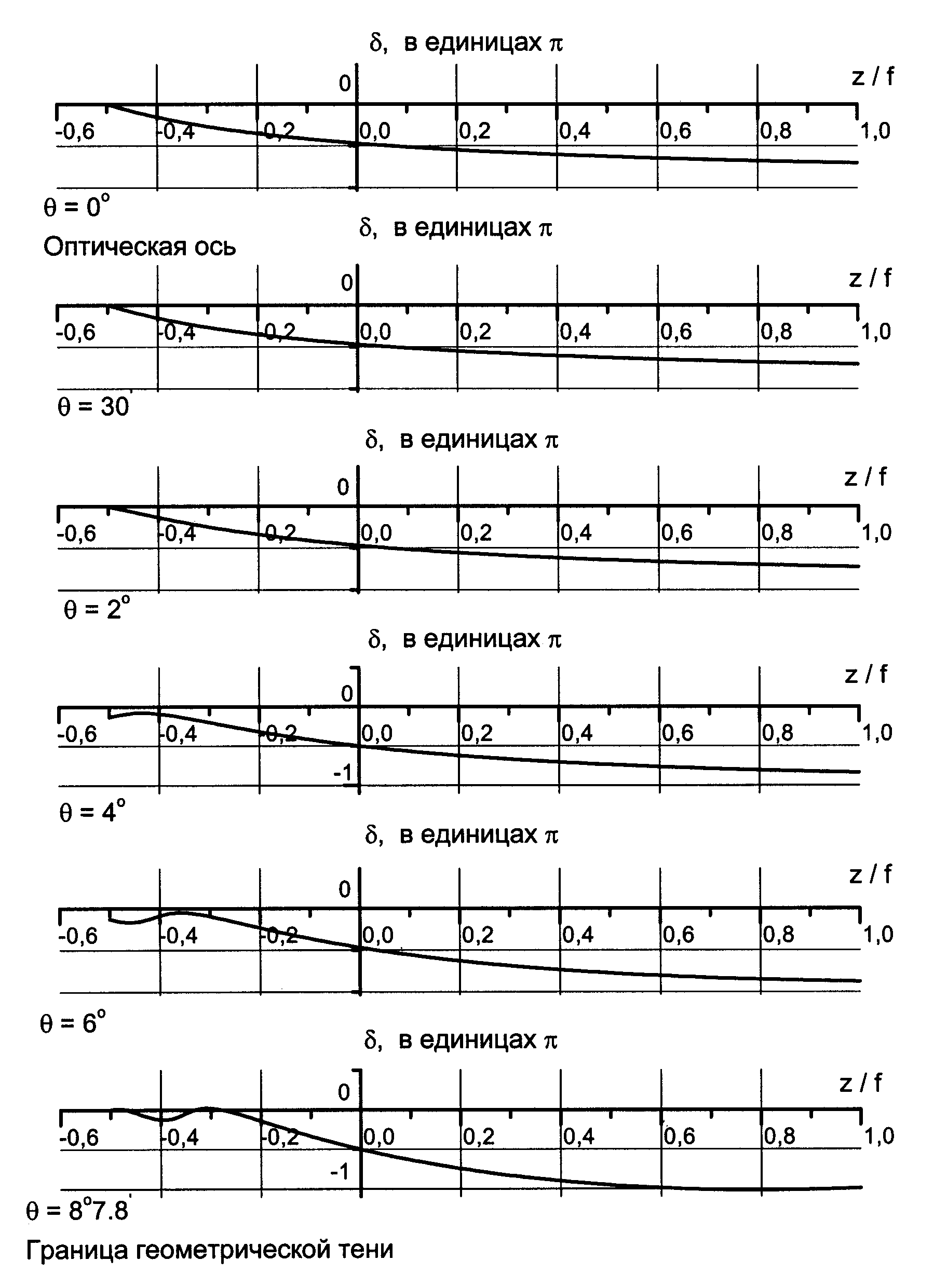
Рис. 2.10. Фазовая аномалия при N = 1.0

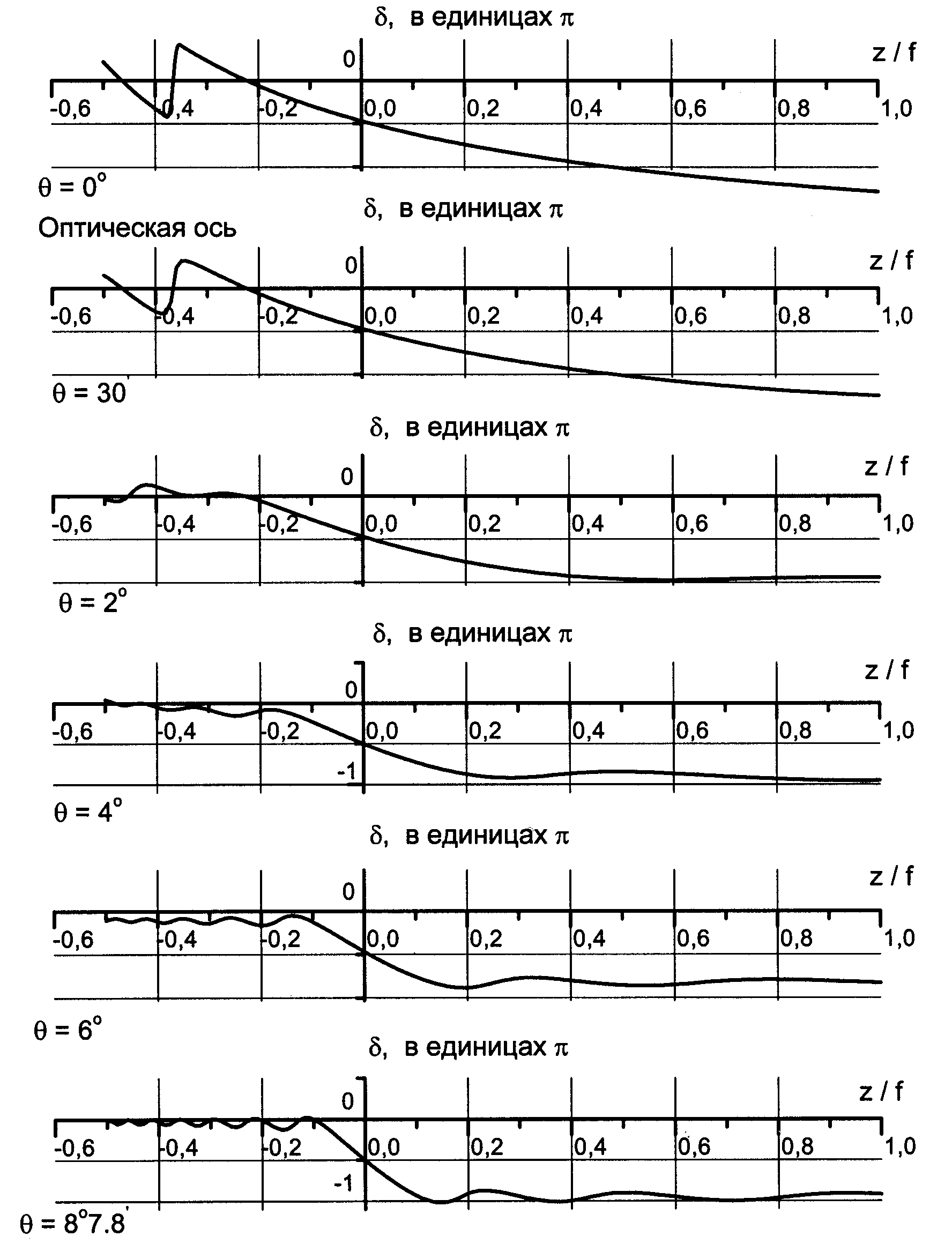
Рис. 2.11. Фазовая аномалия при N = 3.46

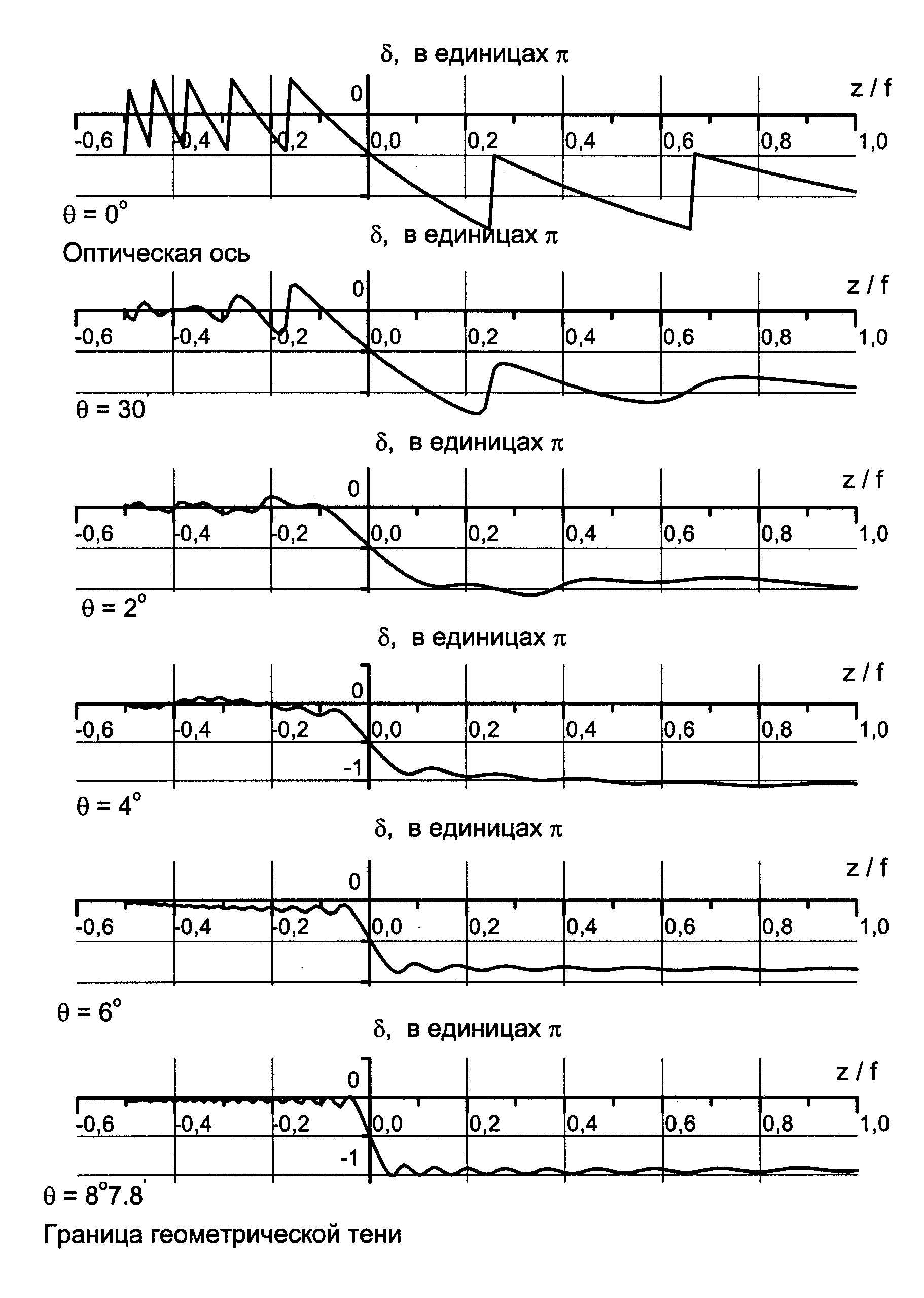
Рис. 2.12. Фазовая аномалия при N = 10

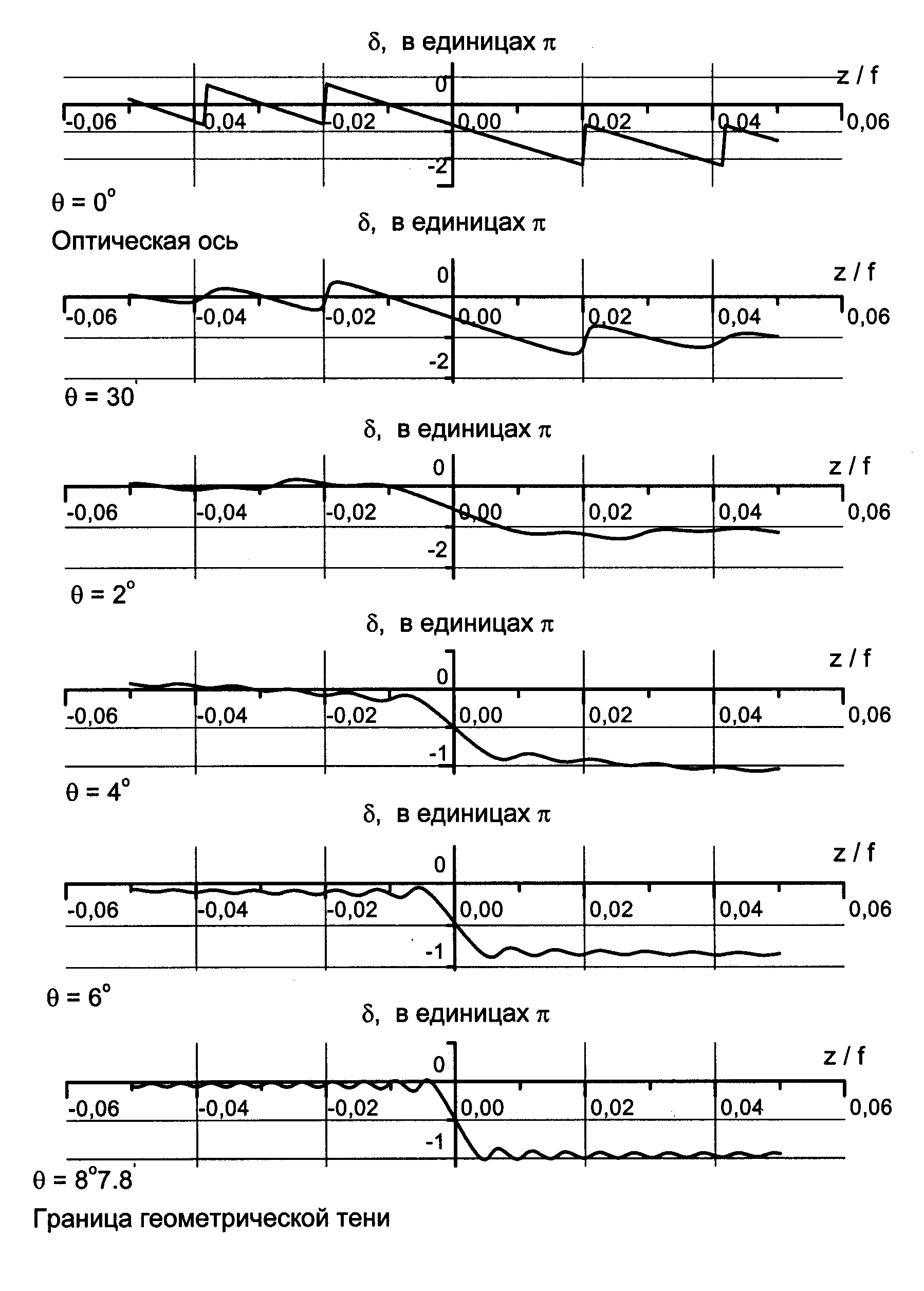
Рис. 2.13. Фазовая аномалия при N = 100