Распределение интенсивности в плоскостях, параллельных плоскости Гаусса
Выражение (2.46) является общим и позволяет вычислить значения интенсивности для любой точки в окрестности параксиального фокуса путем численного интегрирования. При этом стоит подробно рассмотреть случай экспоненциального (гауссового) закона распределения амплитуды, как наиболее важный с точки зрения практических задач лазерной и микроволновой оптики [17].
Дифракционный интеграл в этом случае имеет вид
(2.57)
Рассмотрим отдельно интеграл:
,
где
и, следовательно,
.
Нормируем на величину поля на оси:
;
;
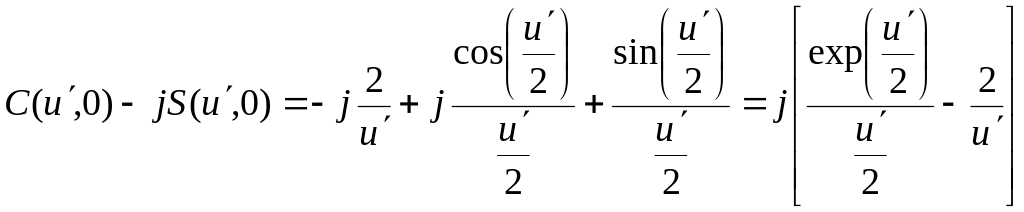Рассмотреть закономерности эволюции распределения интенсивности с изменением параметра s удобнее всего в плоскости Гаусса. (u = 0). В этом случае u' = -js и
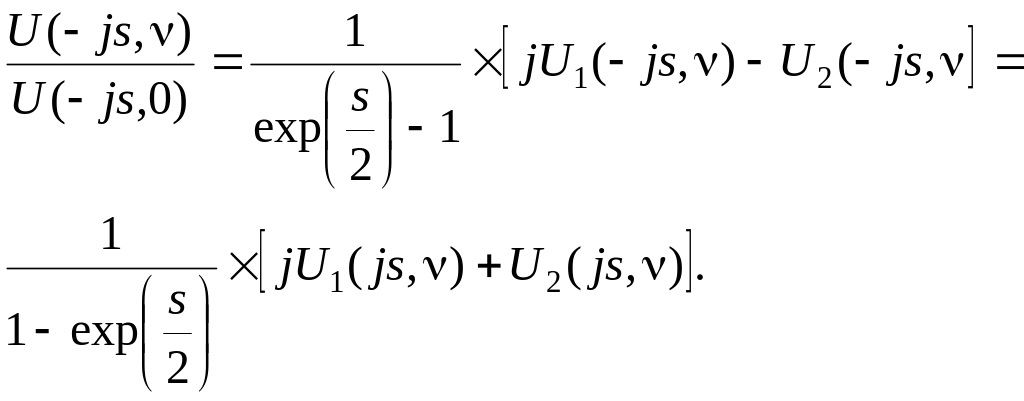(2.58)
Графики распределения
относительной интенсивности в плоскости
Гаусса представлены на рис. 2.21–2.25.
Распределение, изображенное на рис. 2.21
– хорошо известное распределение Эйри
(s = 0).
Буквы A, A', B, B'... обозначают
минимумы и максимумы распределения,
которые расположены в точках, являющихся
корнями уравнений
и
,
соответственно. Рис. 2.22–2.25 демонстрируют
эволюцию распределения с ростом параметра
s.
В дальнейшем изложении данный процесс
будет описан в терминах «движения»
максимумов и минимумов.
Для распределения, изображенного на рис. 2.22, s = 4.5. Видно, что точка A движется к A' с ростом s. При этом интенсивность в первом дифракционном порядке уменьшается. Положение же остальных дифракционных минимумов и максимумов практически не меняется. При s = 5.25 точки A и A' совмещаются друг с другом и с точкой B, «зажатой» между ними (рис. 2.23) Иными словами, два первых темных кольца сливаются, первый дифракционный порядок исчезает, а нулевой становится шире.
Слияние происходит, когда U(v) = 0 и dU(v)/dv = 0.
Подставив в эти условия (2.58), учтем, что
и получим:
(2.59)
Эти равенства
будут выполнены только тогда, когда
,
т.е.
,
где
– корни уравнения
.
Это означает, что слияние происходит в
точке A'
– втором минимуме распределения Эйри,
для которого
.
Подставив
в уравнения (2.59), получим:
. (2.60)
Индексы 1,k
при s
означают, что при данном s
происходит слияние дифракционных
колец в точке
.
Уравнение (2.60) имеет действительные и
неотрицательные решения при значениях
индекса k = 2,4,6...
, это означает, что слияние происходит
на месте четных темных колец. На рис.
2.24 точка B движется к B', идет
процесс слияния двух соседних дифракционных
порядков. На рис. 2.25 точка слияния B
является точкой перегиба кривой, т.е:
dU(v)/dv=0
и d
U(v)/dv
=0.
Подставляя в эти условия (2.58), получим
систему уравнений, аналогичную (2.59):
(2.61)
Точно так же должно выполняться условие , и итоговое уравнение примет вид:
k=2,4,6…
Слияние дифракционных
порядков происходит в точках
,
т.е. на месте четных светлых колец
распределения Эйри. Уравнения для
нахождения
и
могут быть решены численными методами
на компьютере. Результаты решения
сведены в табл. 2.1 и 2.2:
Таблица 2.1. Значения параметра неравномерности s и точки слияния первых четырех темных дифракционных колец.
k |
|
|
2 |
5,2548 |
7.01559 |
4 |
11,2059 |
13.32369 |
6 |
17,2868 |
19.61586 |
8 |
23,4245 |
25.90367 |
Таблица 2.2. Значения параметра неравномерности s и точки слияния первых четырех светлых дифракционных колец.
k |
|
|
2 |
6.4362 |
8.41724 |
4 |
12.5351 |
14.79595 |
6 |
18.6799 |
21.11700 |
8 |
24.8538 |
27.42057 |
С дальнейшим увеличением s все более высокие дифракционные порядки вовлекаются в процесс слияния с нулевым, и распределение стремится к гауссову, что очевидно, если интерпретировать s как 2(A/w)2, где w – радиус гауссова пучка на выходном зрачке. При больших s A >> w, и дифракционные эффекты незначительны.
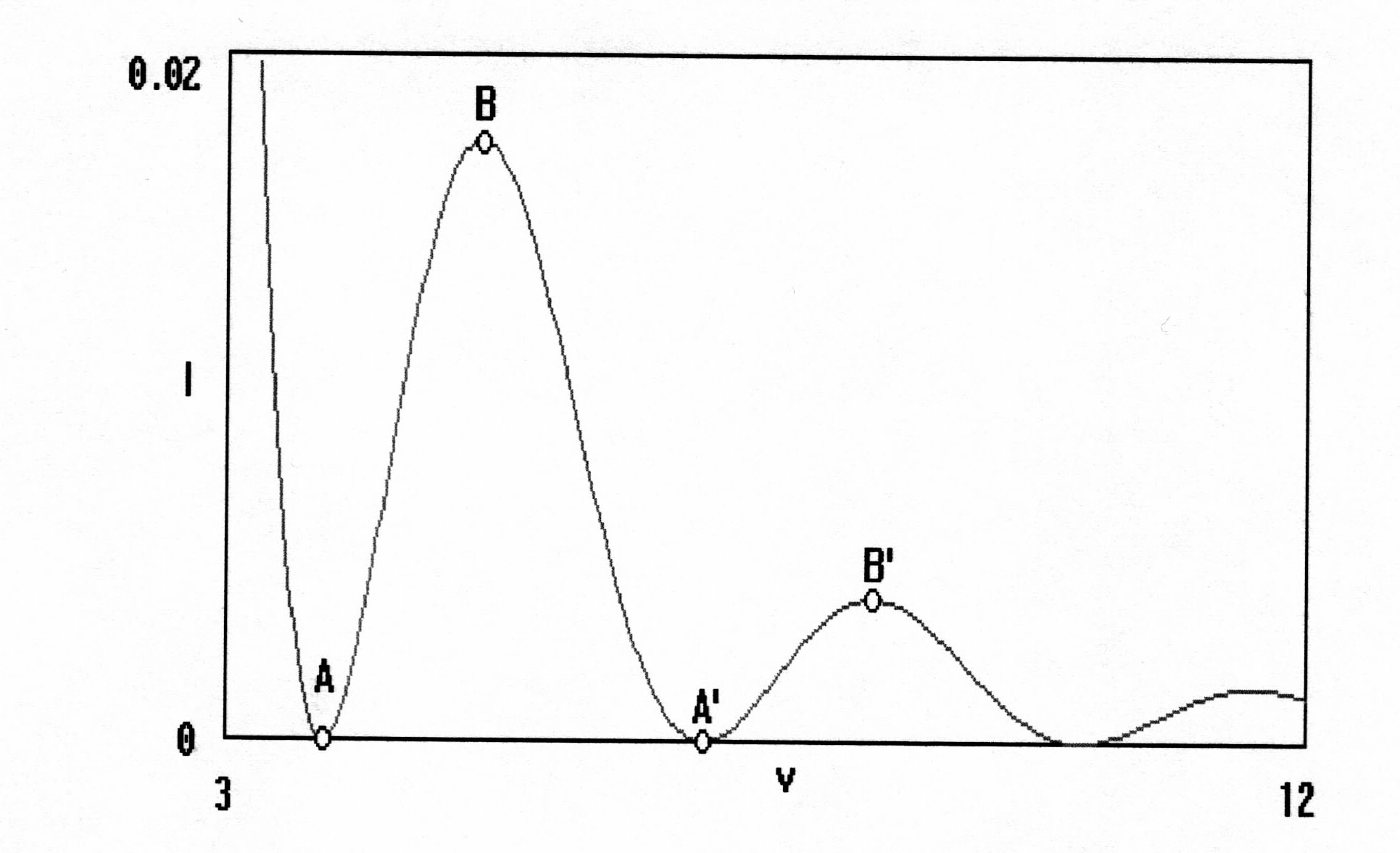
Рис. 2.21. Фрагмент распределения относительной интенсивности гауссова пучка, S = 0.
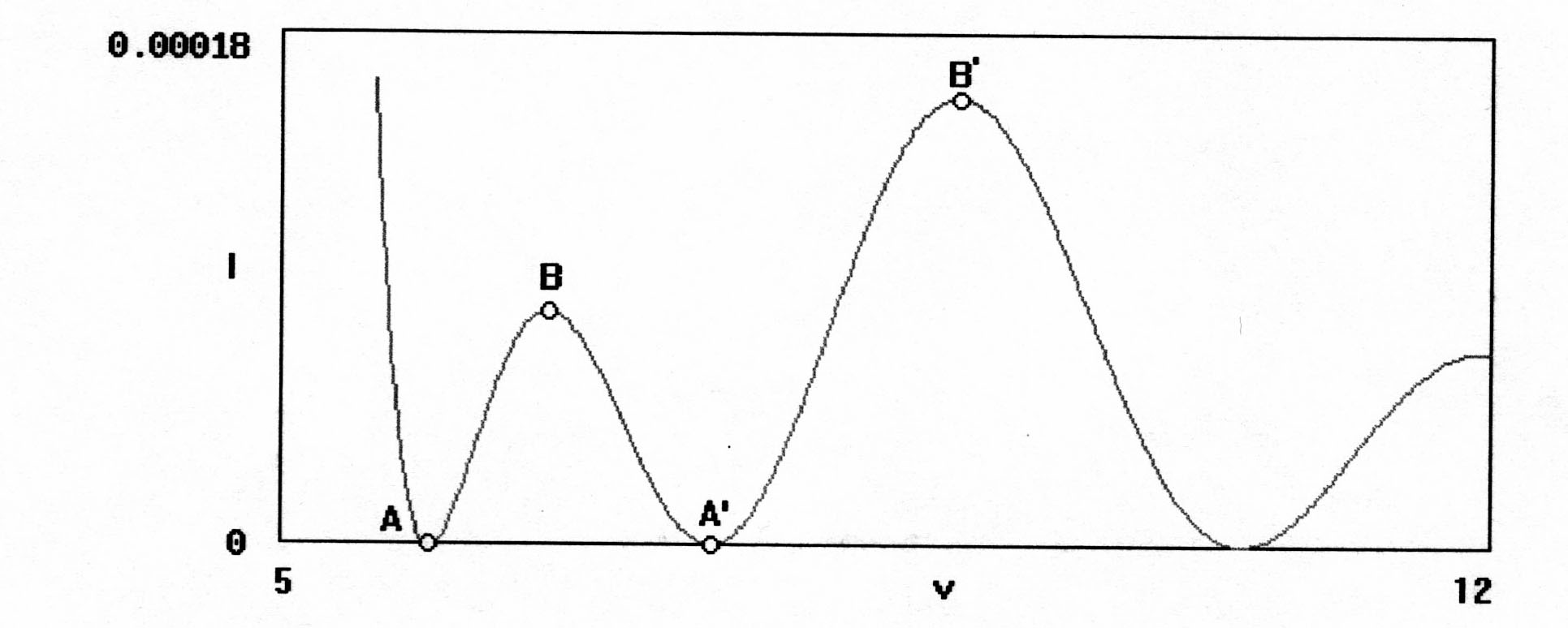
Рис. 2.22. Фрагмент распределения относительной интенсивности гауссова пучка, S = 4.5
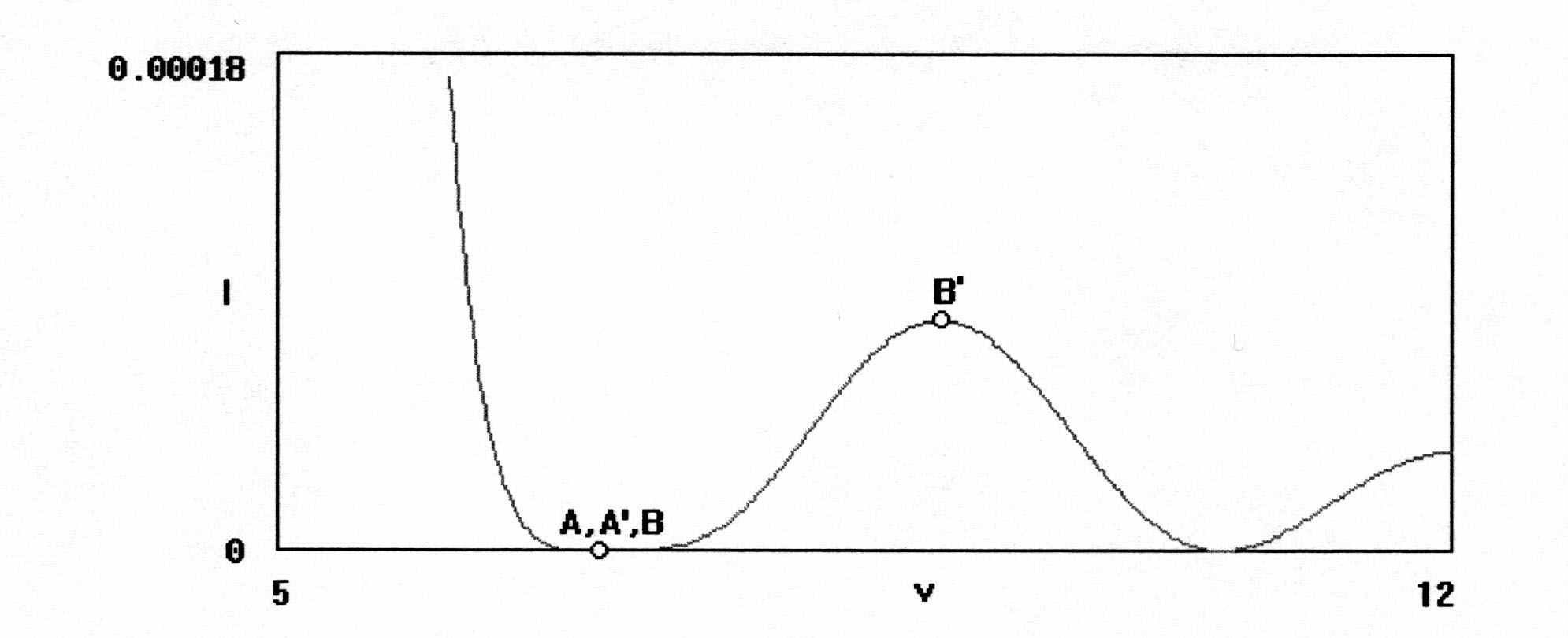
Рис. 2.23. Фрагмент распределения относительной интенсивности гауссова пучка, S = 5.25
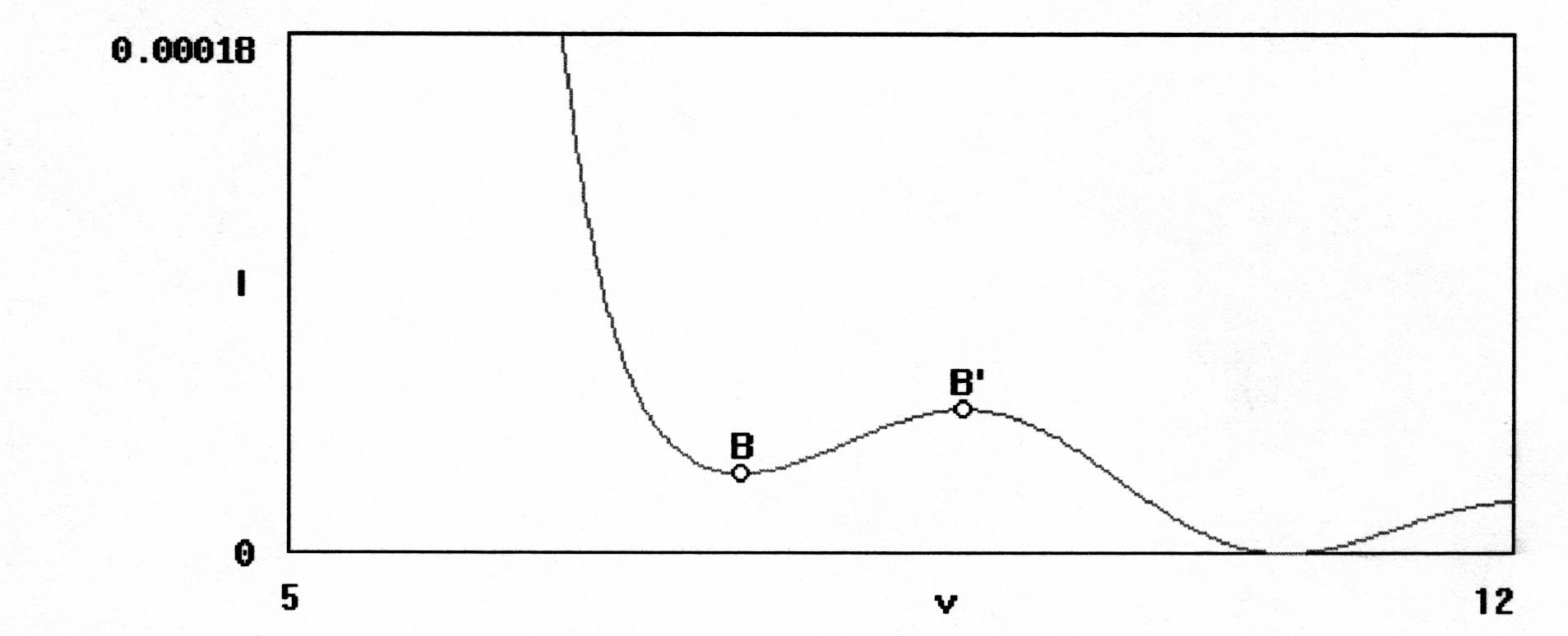
Рис. 2. 24. Фрагмент распределения относительной интенсивности гауссова пучка, S = 6
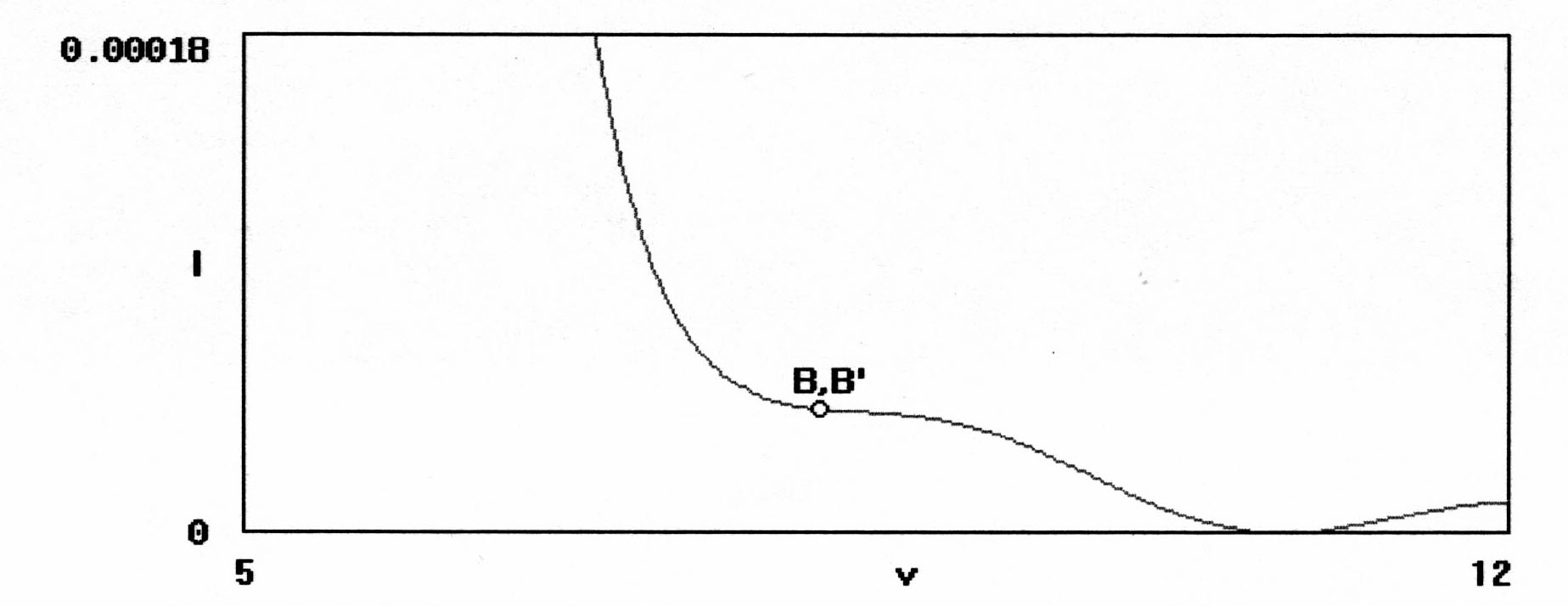
Рис. 2.25. Фрагмент распределения относительной интенсивности гауссова пучка, S = 6.5
Для тригонометрического закона эволюция распределения интенсивности в плоскости Гаусса в общем следует той же закономерности, что и аксиальное распределение (рис. 2.26). Основное различие заключается в том, что перегиб возникает при значении s = 1.5, и, кроме того, не наблюдается роста интенсивности во вторичных дифракционных порядках при уменьшении интенсивности в нулевом, т.е. при увеличении значения s максимальное значение интенсивности в распределении монотонно уменьшается.
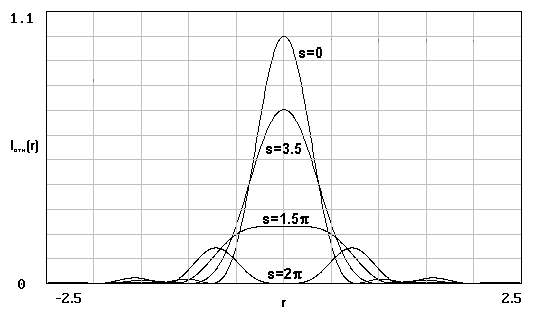
Рис. 2.26 Распределение относительной интенсивности в плоскости Гаусса для тригонометрического закона (N = 1000)
Далее, следует отметить, что с ростом s расстояние между первыми дифракционными порядками увеличивается. Для параболического закона также наблюдается сходство распределения интенсивности в плоскости Гаусса и аксиального распределения (рис. 2.27).
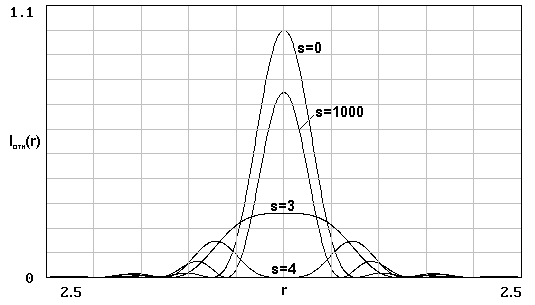
Рис. 2.27. Распределение относительной интенсивности в плоскости Гаусса для параболического закона ( N = 1000)
Так же, как и для тригонометрического закона, перегиб возникает при другом значении s, а именно s = 3. Аналогично аксиальному распределению, существует предельная кривая (на рис. 2.27 с индексом s = 1000), но переход к этой кривой осуществляется иначе. Нового перегиба и повторения формы распределения не возникает, когда s становится больше 4, начинается рост нулевого порядка, и в пределе относительная интенсивность достигает значения 0.75.
На рис. 2.28–2.33
представлен ряд изофот в плоскостях,
параллельных плоскости Гаусса, построенных
для различных законов распределения
амплитуды, при этом соблюдалось условие
равенства потоков, для выполнения
которого были взяты следующие значения
параметров неравномерности:
.
Рис. 2.28. Изофоты поля в геометрической фокальной плоскости (u = 0, гауссовский закон изменения амплитуды в зрачке, s = 3.22, число Френеля N = 6.33)
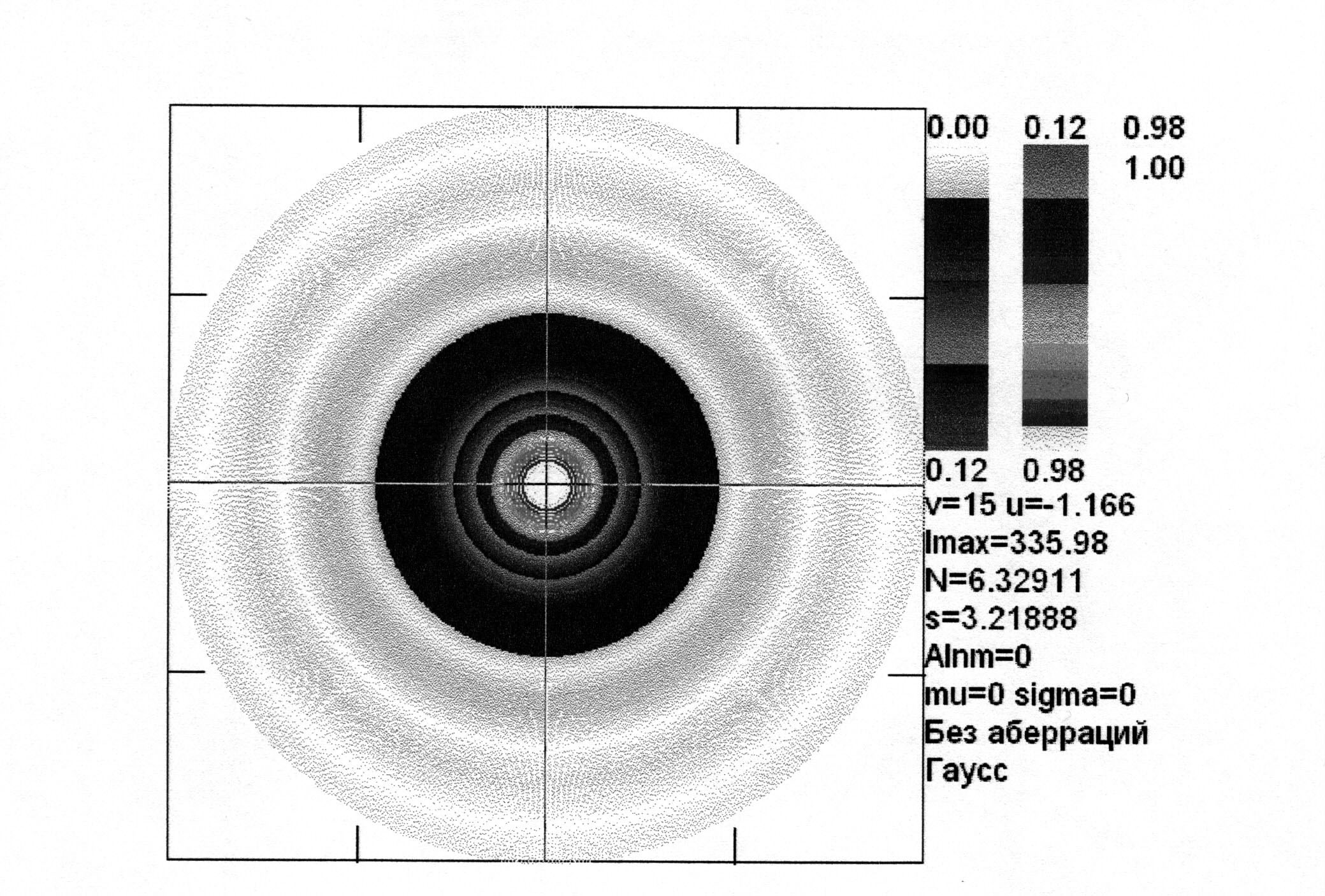
Рис. 2.29. Изофоты поля в дифракционном фокусе (u = -1.66, гауссовский закон изменения амплитуды в зрачке, s = 3.22, число Френеля N = 6.33)
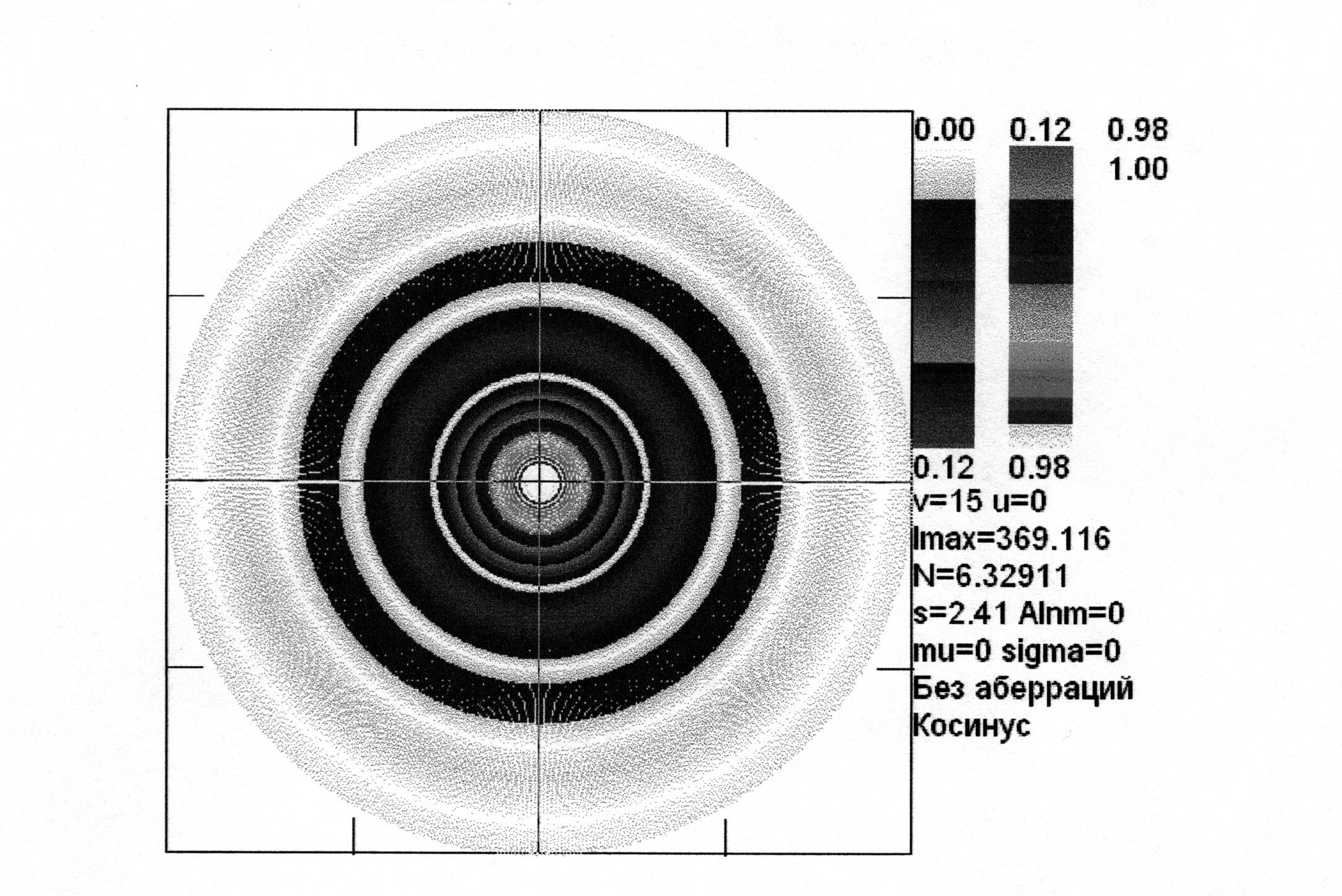
Рис. 2.30. Изофоты поля в геометрической фокальной плоскости (u =0, тригонометрический закон изменения амплитуды, s = 2.41, N = 6.33)
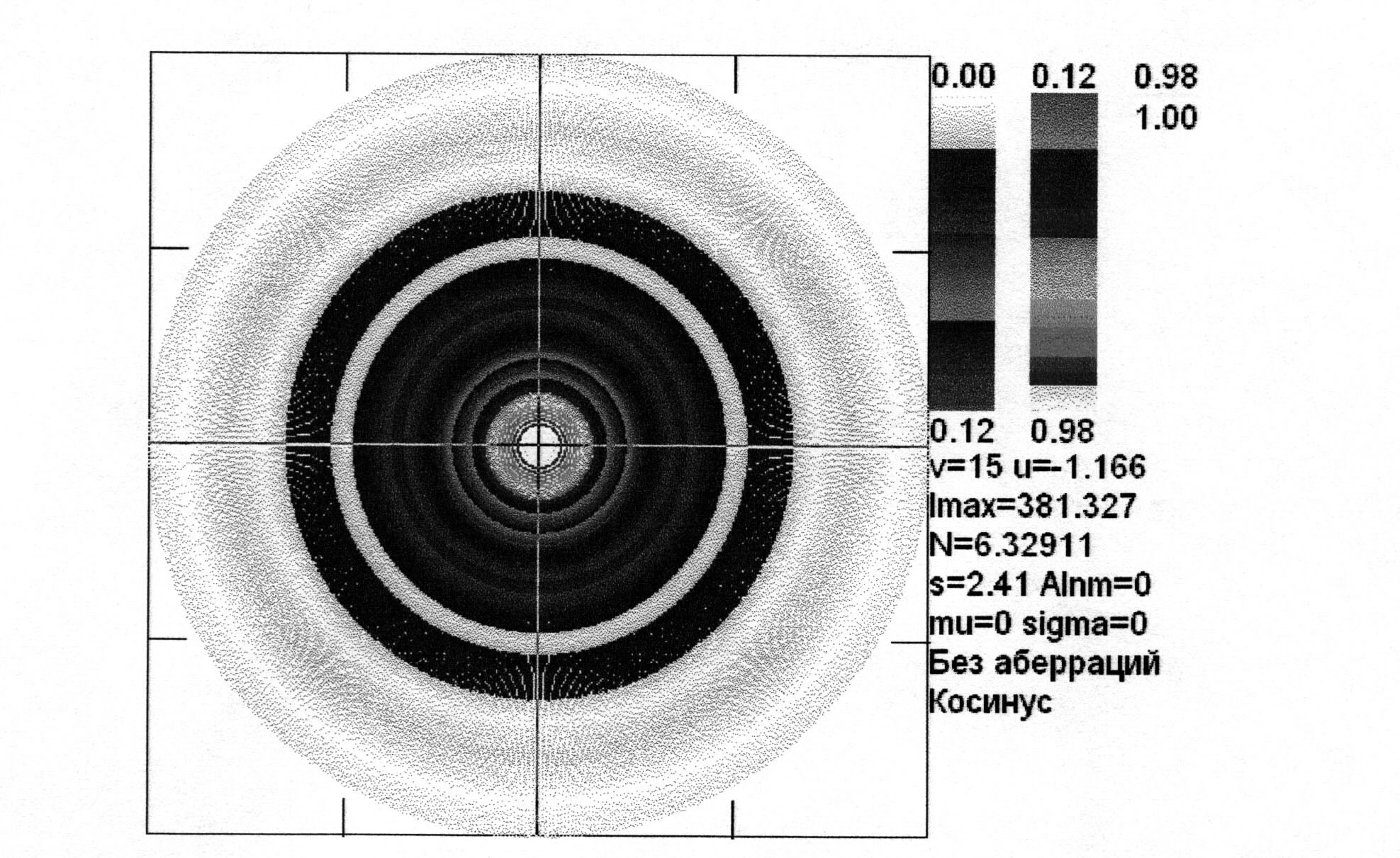
Рис. 2.31. Изофоты поля в дифракционном фокусе (u =-1.66, тригонометрический закон изменения амплитуды, s = 2.41, N = 6.33)
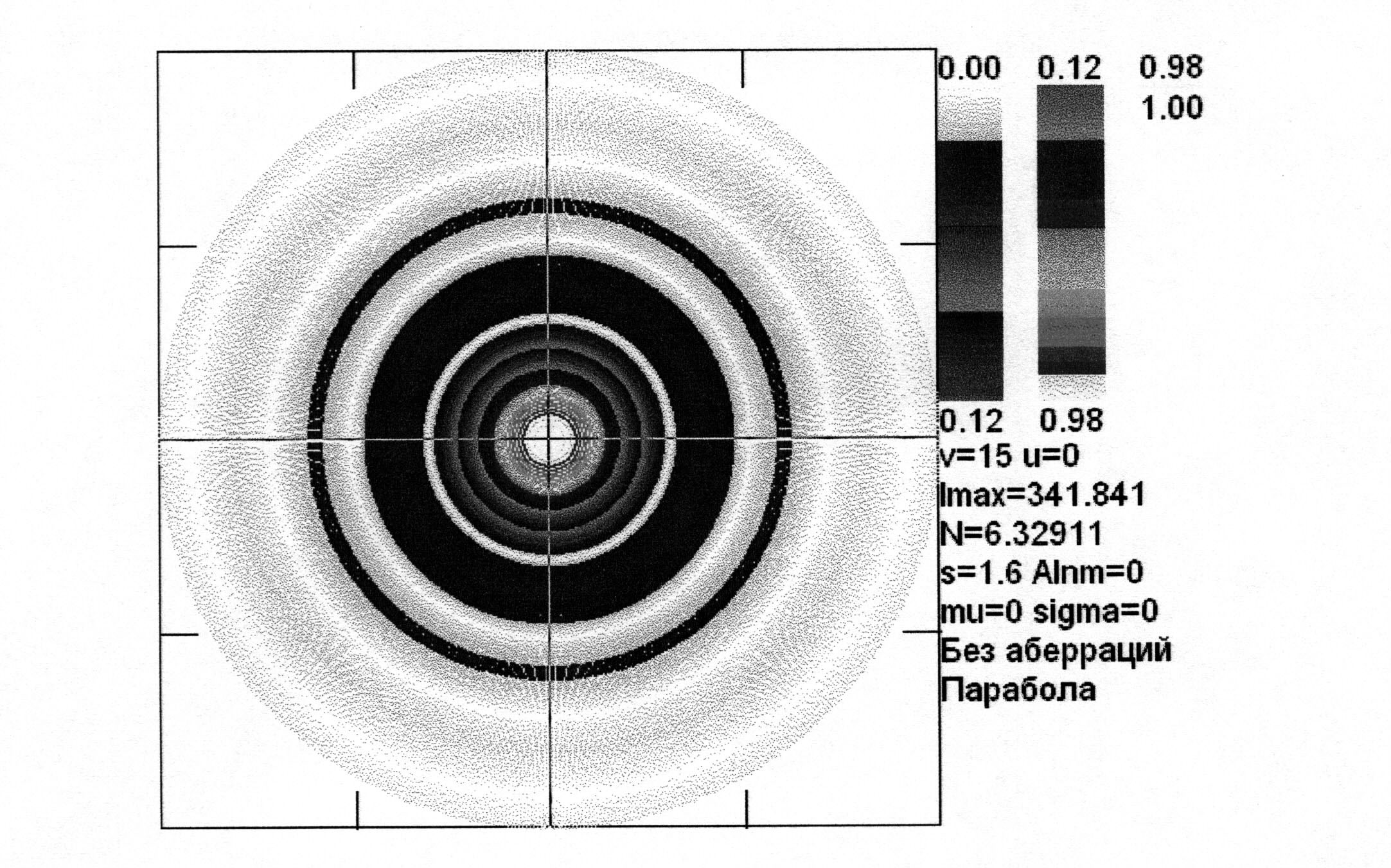
Рис. 2.32. Изофоты поля в геометрической фокальной плоскости (u=0, параболический закон изменения амплитуды, s = 1.6, N = 6.33)
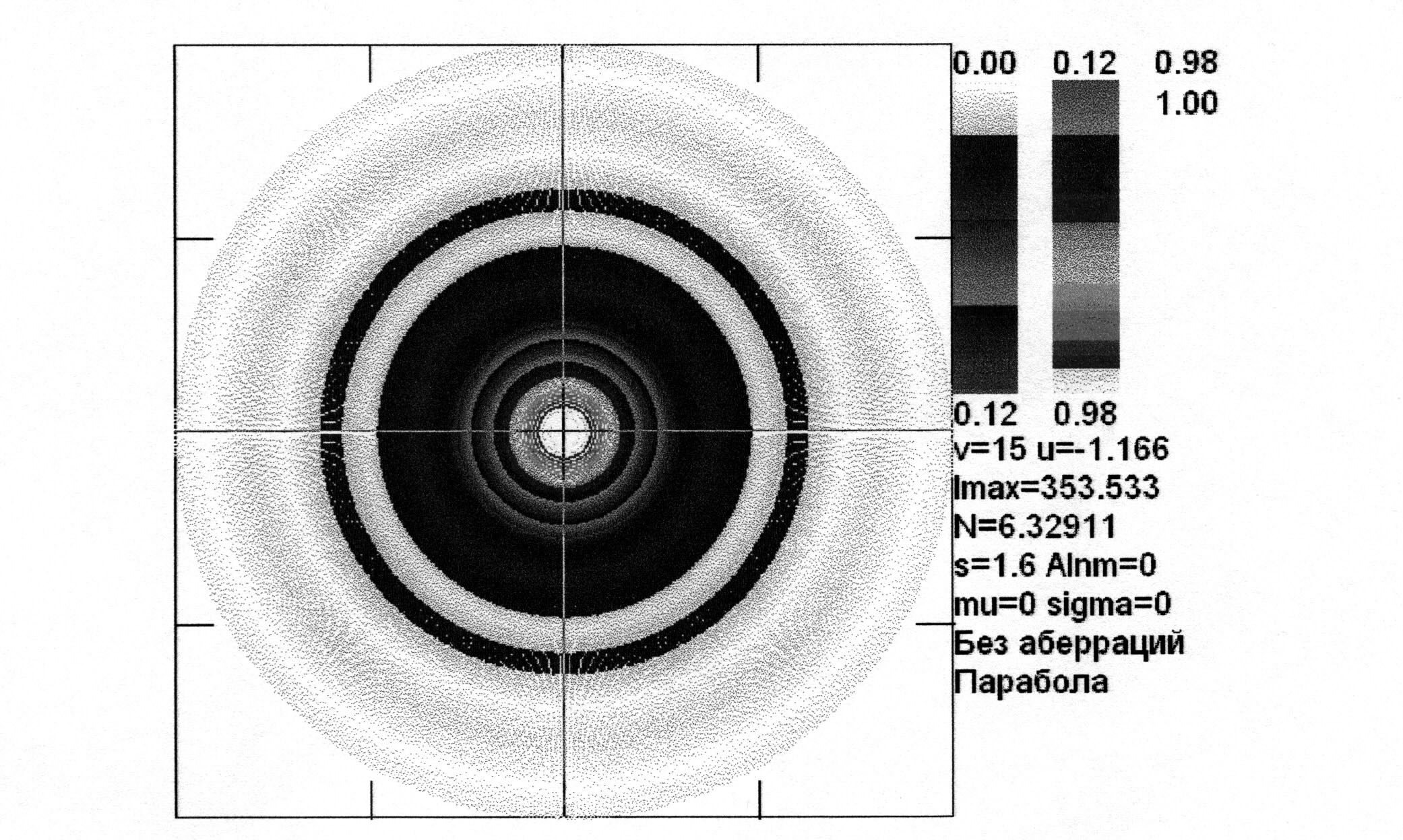
Рис. 2.33. Изофоты поля в дифракционном фокусе (u= -1.66, параболический закон изменения амплитуды, s = 1.6, N = 6.33)
Влияние распределения амплитуды дифрагирующего пучка на характер «упаковки» поля в фокальном объеме наиболее наглядно прослеживается при анализе меридионального сечения. На рис. 2.34–2.43 приведены результаты расчетов распределения интенсивности в меридиональной плоскости оптической системы с большим числом Френеля (N = 1000) для трех рассмотренных законов: гауссовского, тригонометрического и параболического, при разных значениях параметров неравномерности.
Рис. 2.34. Гауссовский закон, s=3, N=1000
Рис. 2.35. s=5, N=1000
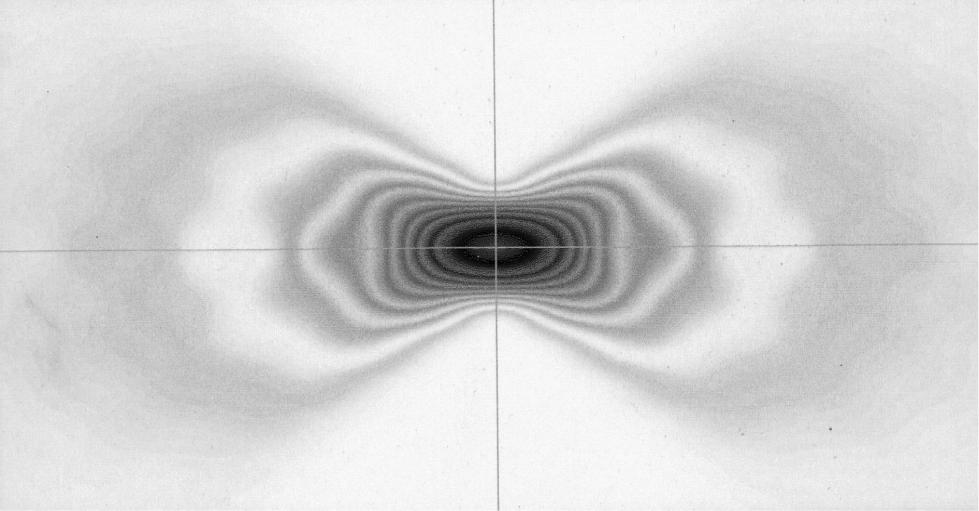
Рис. 2.36. s=7, N=1000
Рис. 2.37. s=10, N=1000
Рис. 2.38. Тригонометрический закон, s=4
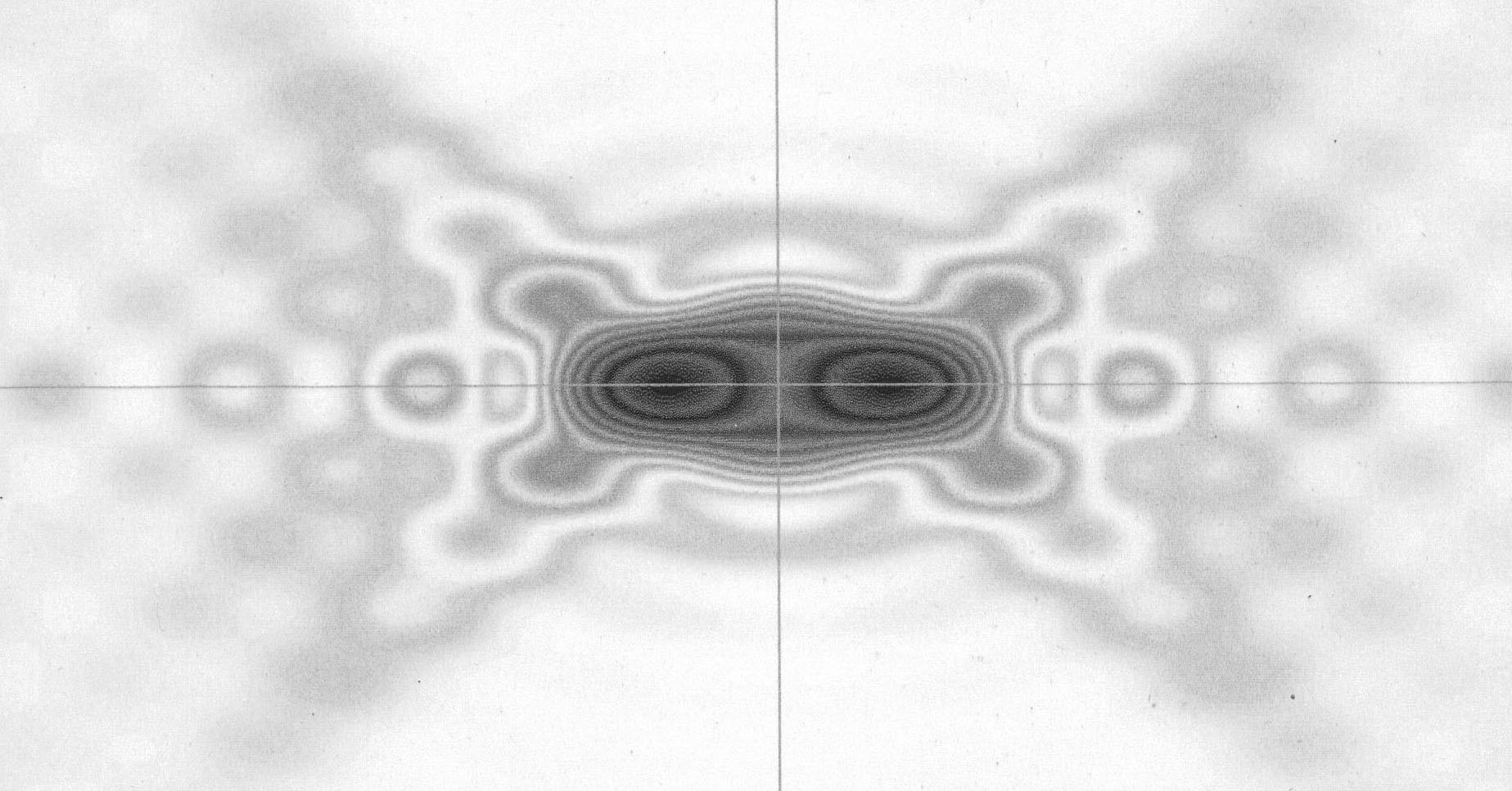
Рис. 2.39. s=1,5, N=1000
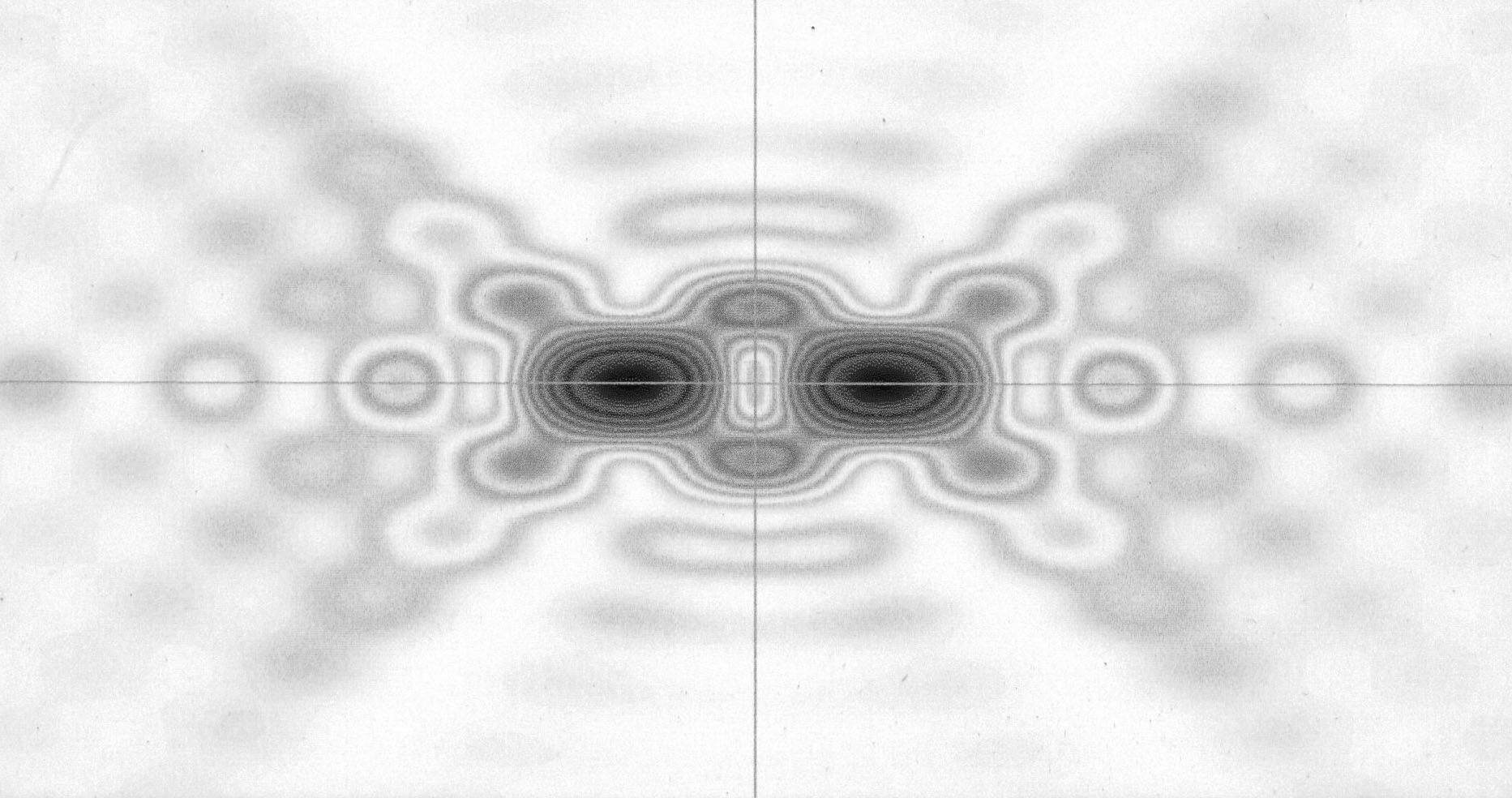
Рис. 2.40. s=2, N=1000
Рис. 2.41. s=4, N=1000
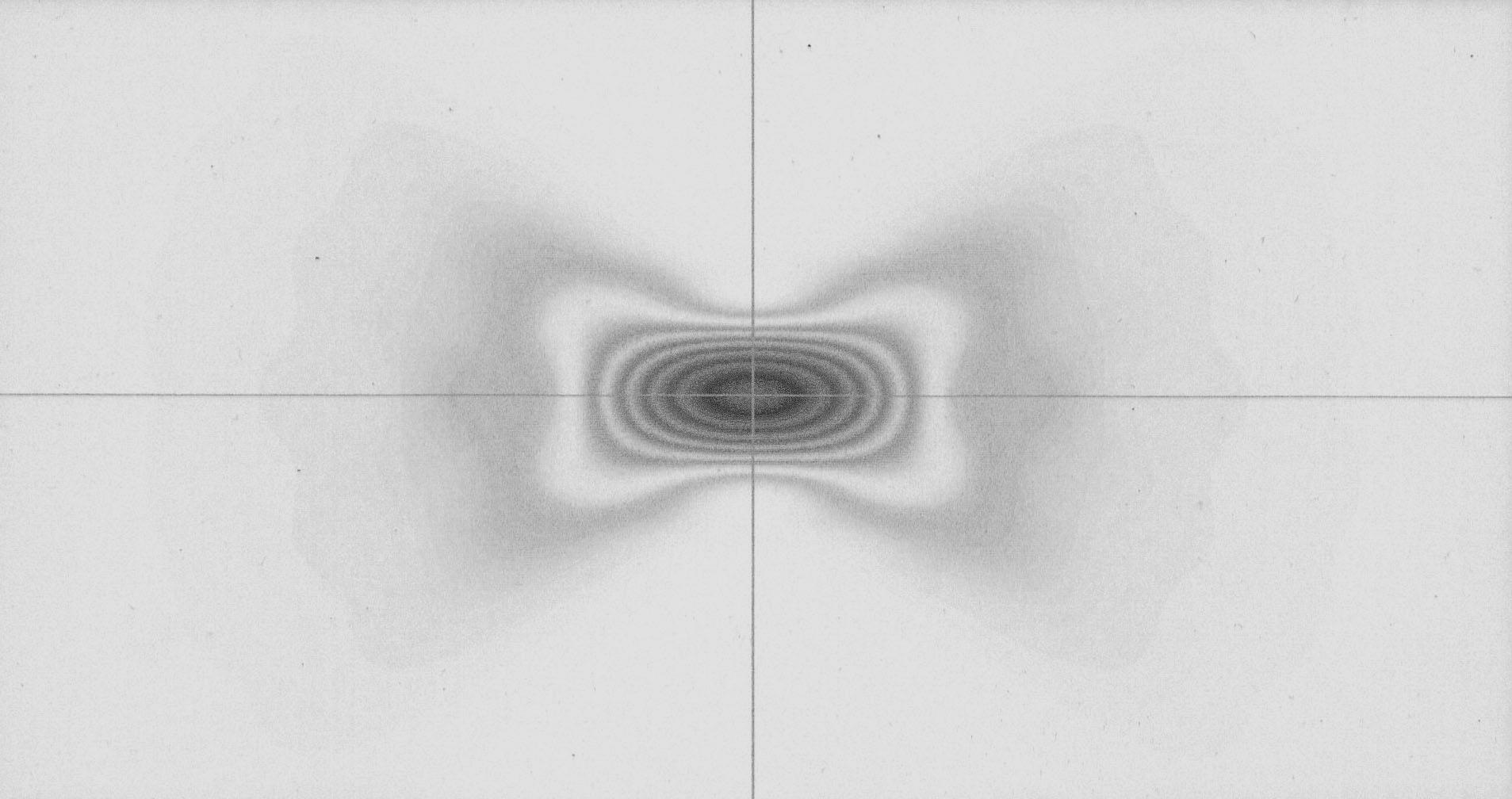
Рис. 2.42 Параболический закон, s=2, N=1000
Рис. 2.43. s=3, N=1000
Рис. 2.44. s=4, N=1000