2. Дифракция неоднородной сходящейся сферической волны. Влияние аберраций оптической системы.

При проектировании и эксплуатации микроволновых и лазерных оптических систем, как правило, приходится сталкиваться с ситуацией, отличной от описанной в предыдущем разделе. Оптическая система трансформирует ограниченный волновой пучок, сформированный рупорной микроволновой антенной или лазерным источником. В качестве примера на рис. 2.14 представлены результаты измерения плотности мощности излучения в выходном зрачке микроволнового объектива.

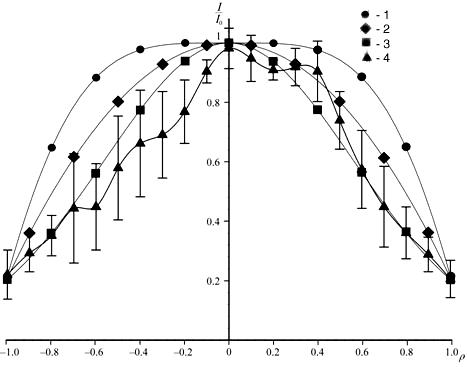
Рис. 2.14. Относительное распределение плотности мощности в выходном зрачке микроволнового объектива (кривая 4).

Источником излучения служил клистронный генератор, работающий в диапазоне 8мм, сигнал от которого поступал в пирамидальную рупорную антенну с раскрывом 8080 мм , снабженную корректирующей линзой. Объектив был выполнен из полистирола и имел следующие характеристики:

– радиус выходного зрачка, мм a = 295  1;

– фокусное расстояние, мм f =970  90.

В качестве приемной антенны использовался открытый срез волновода, соединенный с детекторной головкой. Сканирование приемной антенны осуществлялось в плоскости выходного зрачка вдоль его диаметра. Усиленный низкочастотный сигнал регистрировался на двухкоординатном самописце. Измерения проводились при фиксированной настройке генератора на длину волны  = (8.390.02) мм. Неравномерный характер распределения поля на зрачке объясняется диаграммой направленности рупорной антенны, а разброс измеренных значений связан с выбором рабочей зоны генерации клистрона и положением рабочей точки на зоне генерации, определяемыми напряжением на отражателе и током резонатора клистрона. Временная нестабильность практически не влияла на изменение распределения. Из приведенного графика видно, что амплитуда поля в выходном зрачке оптической системы существенно меняется от центра к краю, уменьшаясь в 5 раз. Предположительно, этот факт должен сказаться на характере дифракционного поля в фокальном объеме микроволновой системы.

При вычислении дифракционного интеграла (2.4) определим поле в зрачке в виде неоднородной сходящейся сферической волны, т.е. волновой фронт имеет радиус R, поверхность равных фаз не совпадает с поверхностью равных амплитуд и A = A().

Предположим, что распределение амплитуды может быть представлено одним из следующих законов [47]:

(2.43)

(2.44)

(2.45)

Здесь (2.43) – экспоненциальный (гауссов) закон; (2.44) – тригонометрический (синусоидальный) закон; (2.45)  – параболический закон; s , s и s – параметры неравномерности. При равенстве параметров s нулю A = const и все три случая сводятся к ранее рассмотренной задаче дифракции однородной волны. Выбор указанных законов изменения амплитуды поля на выходном зрачке объясняется удобством аппроксимации реальных распределений. Так, экспоненциальный закон позволяет аппроксимировать «острое» распределение с резким падением амплитуды от центра к краю (кривая 3 на рис. 2.14). «Трапециевидное» (кривая 1) распределение с пологой вершиной может быть аппроксимировано тригонометрическим законом. В промежуточных случаях можно воспользоваться параболическим законом (кривая 2). Кроме того, с помощью тригонометрического закона можно задать поле на выходном зрачке в виде системы колец со сдвигом фазы в кольцах на .

В цилиндрической системе координат, с учетом ранее рассмотренных условий, выражение для комплексной амплитуды поля в окрестности параксиального фокуса можно записать в виде

(2.46)

Определив A() и пользуясь методами численного интегрирования, можно рассчитать поле U(Q) и интенсивность I(Q) = U(Q)U^*(Q).