2. Гипергеометрические моды

Комплексная амплитуда параксиального свето­вого поля в цилиндрической системе коор­динат удовлетворяет уравнению типа Шредингера:

, (2.189)

где волновое число света с длиной волны .

Уравнению (2.189) удовлетворяют функции, образующие ортонормированный базис:

, (2.190)

где непрерывный и дис­кретный параметры, от которых зависят функции (2.190) и которые будем называть номерами моды; - аналог длины Релея, – параметр моды, аналогич­ный радиусу гауссова пучка, хотя здесь он имеет другой смысл; – гамма функция; – вырожденная или конфлюэнтная гипер­геометрическая функция:

, (2.191)

где . Из (2.191) видно, что – это целая аналитическая функция. В случае (2.190) и тогда уравнение (2.191) является одномер­ным преобразованием Фурье от ограниченной функции на отрезке . По теореме Шеннона асимптотически при период модуляции функции (2.190) (т.е. расстояние между соседними максимумами или минимумами) равно . При больших значениях аргумента имеет место асимптотика . Такое поведение модуля функции (2.190) совпадает с асим­птотикой функции Бесселя. Кроме того, нули вы­рожденной гипергеометрической функции близки к нулям функции Бесселя

: .

Реализовать световые пучки (2.190), которые будем называть гипергеометрическими модами, можно с помощью оптического элемента, имеющего функцию пропускания:

. (2.192)

При освещении оптического элемента (2.192), распо­ложенного в плоскости , неограниченной плоской волной на расстоянии сформируется световое поле с комплексной амплитудой (2.190). Энергия световых полей (2.190) и (2.192) не ограничена, как и у моды Бесселя

,

которая также удовлетворяет уравнению (2.189). Поэтому на прак­тике для реализации моды (2.190) оптический элемент (2.192) следует ограничивать кольцевой диафрагмой. При этом на конечном расстоянии , где - больший радиус кольцевой диафрагмы, будет эф­фективно формироваться мода (2.190).

Световое поле (2.190) при распространении сохра­няет свою структуру и меняется только масштаб­но. Поперечное распределение интенсивности гипергеометрической моды (2.190) представляет собой набор концентриче­ских световых колец, радиусы которых удовле­творяют условию:

, (2.193)

где - постоянные, зависящие от номера кольца да и от номеров моды . Из (2.193) следует, что радиусы колец увеличиваются с ростом как . Из соотношения: следует, что фаза гипергеометрической функции равна : . Инте­ресно, что эта фаза не зависит от номеров моды . Тогда можно записать выражение для фазы гипергеометрической моды:

. (2.194)

Формула (2.190) позволяет рассчитывать идеаль­ные (бесконечные) гипергеометрические моды. Однако при генера­ции этих мод используется оптический элемент конечного размера, поэтому при моделировании формирования гипергеометрических мод использовалось преобра­зование Френеля:

(2.195)

от входной функции (2.192).

На рисунках 2.65 – 2.67 показаны распределения ин­тенсивности и фазы различных гипергеометрических мод и их су­перпозиций, рассчитанные по формулам (2.190) и (2.195), на расстояниях мм и мм. Пара­метры расчета: длина волны нм, размер изображений - мм, число отсчетов - .

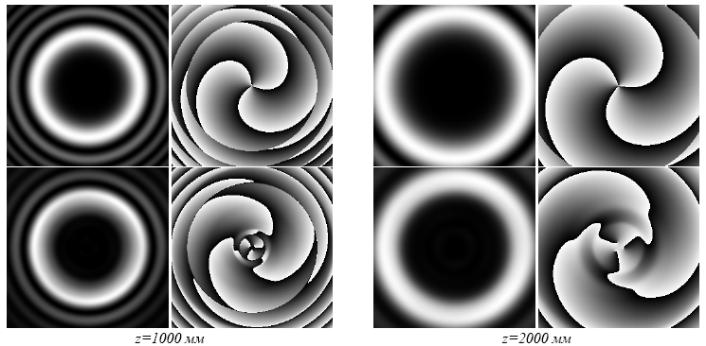
Рис. 2.65. Распределения интенсивности и фазы гипергеометрической моды , рассчитанное по формуле (2.190) (верхняя строка) и по формуле (2.195) (нижняя строка) на различных расстояниях [28]

Рис. 2.66. Распределения интенсивности и фазы суперпозиции из двух гипергеометрических мод , рассчитанное по формуле (2.190) (верхняя строка) и по формуле (2.195) (нижняя строка) на различных расстояниях [28]

Рис. 2.67. Распределения интенсивности и фазы суперпозиции из двух гипергеометрических мод , рассчитанное по формуле (2.190) (верхняя строка) и по формуле (2.195) (нижняя строка) на различных расстояниях [28]

Среднеквадратичное отклонение распределения интенсивностей для идеальных пучков (формула (2.190) и полученных через преобразование Френеля (формула (2.195)) составило 15-23%.

На рис. 2.68 показаны радиальные сечения интен­сивности гипергеометрической моды на расстояниях z=100 мм и z=200 мм. Видно, что радиусы световых ко­лец увеличиваются с ростом z. На рис. 2.69 приведен график расходимости интенсивности этой моды в зависимости от пройденного расстояния z.

Среднеквадратичное отклонение численных ре­зультатов от аппроксимирующей функции составило 14%.

На рис. 2.70 приведены радиальные сечения интен­сивности гипергеометрических мод с одинаковым параметром и различными индексами на одном и том же рас­стоянии. Видно, что с ростом индекса радиус пер­вого светового кольца увеличивается. Это связано с возрастанием номера винтовой сингулярности, ко­торую содержат гипергеометрические моды.

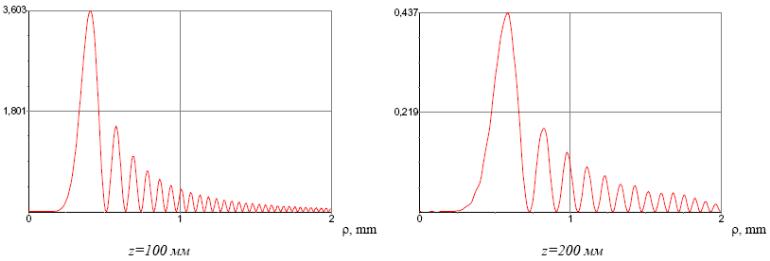
Рис. 2.68. Радиальные сечения интенсивности гипергеометрической моды , рассчитанные по формуле (2.195) на различных расстояниях[28]

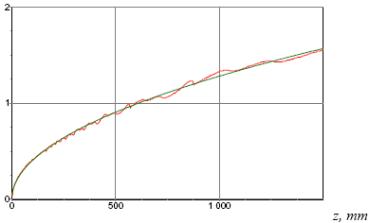
Рис.2.69. График расходимости интенсивности гипергеометрической моды в зависимости от пройденного расстояния z: сплошной линией отображен результат численных расчетов по формуле (2.195), пунктирной – аппроксимация функцией [28]

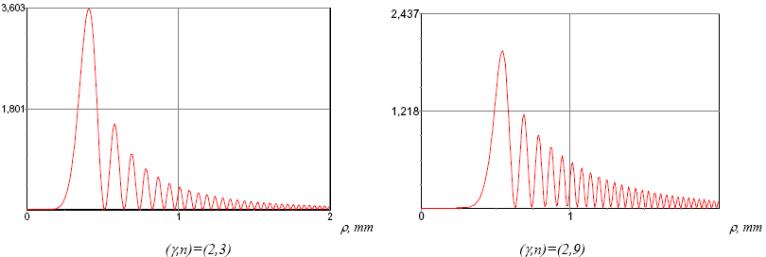
Рис. 2.70 Радиальные сечения интенсивности гипергеометрических мод[28]

Литература к разделу 2.

1. Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую радиофизику и оптику. М.: Наука, 1981. 640 с.

2. Борн М., Вольф Э.. Основы оптики. Пер. с англ. М.: Наука, 1970. 856с.

3. Бухонин Ю.С., Львова Н.А., Смирнов С.А. Исследование распределения поля в области дифракционного фокуса квазиоптических систем дальнего видения // Труды ЛИТМО. Вып. 79. Вопросы квантовой электроники. Л.: ЛИТМО, 1975. С. 6–12.

4. Быков В.П., Силичев О.О. Лазерные резонаторы. М.: ФИЗМАТЛИТ, 2003. 320 с.

5. Ваганов Р.Б. Свойства сфокусированных полей // Р и Э. 1983. Т. 28. Вып. 5. С. 834–842.

6. Гримм В.А., Карасев В.Б., Кузьмин Ю.В., Лосев К.Д., Смирнов С.А. / Под ред. Смирнова С.А. Лазерные и микроволновые оптические системы. СПб. 2005. 232с.

7. Гудмен Дж. Статистическая оптика. М.: Мир, 1988. 528 с.

8. Коротков П.А., Смирнов С.А. Статистический скалярный анализ дифракции в оптических системах с произвольным числом Френеля// Известия Вуз-ов «Приборостроение». 2004. Т.47. Вып. 5. С. 63-71

9. Магурин В.Г., Смирнов С.А.. Влияние амплитудного и фазового распределений на фокусировку лазерного пучка. / Тезисы конференции «Прикладная оптика-96». СПб, 1996.

10. Смирнов С.А., Стафеев С.К. Влияние неравномерности амплитуды на выходном зрачке на вид ФРТ микроволновых оптических систем. // Рук. деп. в ВИНИТИ, № 1085-84, 1984. 14 с.

11. Смирнов С.А.. Поле в области фокуса дифракционно-ограниченной оптической системы микроволнового диапазона. // Рук. деп. в ВИНИТИ, № 1086-84, 1984. 11 с.

12. Смирнов С.А.. Теорема смещения и интенсивность в центре опорной сферы сравнения // Рук. деп. в ВИНИТИ, № 1084-84, 1984. 7 с.

13. Bachynski M.P., Bekefi G. Aberrations in circulary symmetric microwave lenses // Trans. IRE. 1956. AP-4. Р. 412.

14. Bachynski M.P., Bekefi G. Study of optical diffraction images at microwave frequencies // JOSA. 1957. V. 47. Р. 428–438.

15. Erkkila J.H., Rogers M.E. Diffracted fields in the focal volume of a converging wave // JOSA. 1981. V. 71. Р. 904–905.

16. Farnell G.W. Calculated intensity and phase distribution in the image space of microwave lens// Can. J. Phys. 1957. V. 35. Р. 777–783.

17. Farnell G.W. Measured phase distribution in the image space of microwave lens// Can. J. Phys. 1958. V. 36. Р. 935–943.

18. Farnell G.W. On the axial phase anomaly for microwave lenses// JOSA. 1958. V. 48. Р. 643–647.

19. Karman G.P., Beijersbergen M.W., van Duijl A., Bouwmeester D., Woerdman J.P. Airy pattern reorganization and sub-wavelength structure in a focus // Huggens Laboratory. Leiden University. 1997. 23 c. karman@rulhm1.leidenuniv.nl.

20. Karman G.P., Beijersbergen M.W., van Duijl A., Woerdman J.P. Creation and annihilation of phase singularities in a focal field // Optics Letters. 1997. V. 22. № 19. Р. 1503–1505.

21. Li Y. Degeneracy and regeneracy in the axial field of a focused truncated Gaussian beam // JOSA. 1988. V. 5. №. 9. Р. 1397–1406.

22. Li Y. Establishment of the maximum encircled energy in the geometrical focal plane // Opt. Acta. 1984. V. 31. Р. 1107–1118.

23. Li Y., Platzer H. An experimental investigation diffraction patterns in low-Fresnel-number focusing systems // Opt. Acta. 1983. V. 30. Р. 1621–1643.

24. Li Y., Wolf E. Conditions for the validity of Debye integral representation of focused fields // Opt. Commun. 1981. V.39. Р. 205–210.

25. Li Y., Wolf E. Focal shifts in diffracted converging spherical waves // Opt. Commun. 1981. V. 39. Р. 211–215.

26. Li Y., Wolf E. Three-dimensional intensity distribution near the focus in systems of different Fresnel numbers // JOSA. 1984. A 1. Р. 801–808.

27. Taylor C.A., Thompson B.J. Attempt to investigate experimentally the intensity distribution near the focus in the error-free diffraction patterns of cicular and annular apertures // JOSA. 1958. V. 48. Р. 844–850.

28. Котляр В.В., Скиданов Р.В., Хонина С.Н., Балалаев С.А. Гипергеометрические моды // Компьютерная оптика, 2006, № 30, с. 16-22..

29. Хонина С.Н. Простой способ эффективного формирования различных бездифракционных лазерных пучков // Компьютерная оптика, 2009, т. 33, № 1, с. 70-78.

30. Скиданов Р.В. Самовоспроизводящиеся лазерные пучки и их применение // Компьютерная оптика, 2006, № 29, с. 4-23.

1 Это неравенство имеет место для всех стационарных случайных процессов; среднеквадратичное значение и среднеквадратичное отклонение совпадают из-за центрированности процесса.

2 Начиная с этой формулы, в тексте будет встречаться введенная функция , общий вид и разложение в ряд которой дано в конце раздела.

293