1.3.2 Фільтрація зображень

Реальні зображення наряду з корисною інформацією можуть містити різні види завад. Джерелами завад є власні шуми оптичних зчитувачів, погана якість оригіналу, шуми каналів зв'язку тощо.

Найбільш розповсюдженою завадою є так званий адитивний білий шум. Його вплив на зображення полягає в адитивному спотворенні кольору або яскравості. Для ахроматичного зображення (зображення у градаціях сірого) вплив білого шуму можна описати за допомогою формули

(1.11)

Тут – «ідеальне зображення», – зображення з завадами, – білий шум, – розміри зображення.

Крім білого шуму ще однією з поширених завад є імпульсна завада, або як її називають – завада «сіль – перець». Ця завада проявляється у виді окремих пікселів колір яких суттєво відрізняється від кольору пікселів з найближчого оточення.

Найпростішими методами боротьби з завадами є застосування локальних маскових фільтрів. Найбільш поширеним фільтрами є усереднюючий, гаусівський та медіанний.

При фільтрації растрових зображень у якості маски використовується квадратні матриці розміру , тобто з непарною кількістю рядків та стовпчиків. У випадку маски , ця матриця має вид:

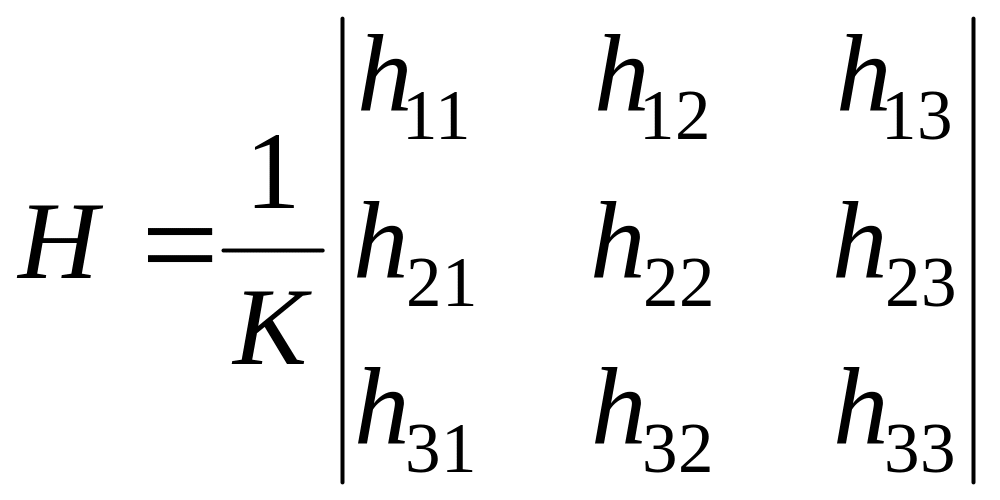(1.12)

Коефіцієнт та значення елементів матриці обираються в залежності від виду фільтру та характеру завад. Елементи цієї матриці, за певних умов, повинні задовольняти умові інваріантності відносно обертань на 90⁰ або 45⁰.

Для визначення кольору центрального пікселу використовується згортка матриці з квадратною частиною (маскою) зображення такого ж розміру. Нехай маска зображення має вид

. (1.13)

Тоді згортка цих матриць буде обчислюватись за формулою

(1.14)

де – значення кольору пікселу на обробленому зображенні.

Для того щоб відфільтрувати зображення обробляються всі його пікселі.

Для усереднюючого фільтру використовуються наступні матриці

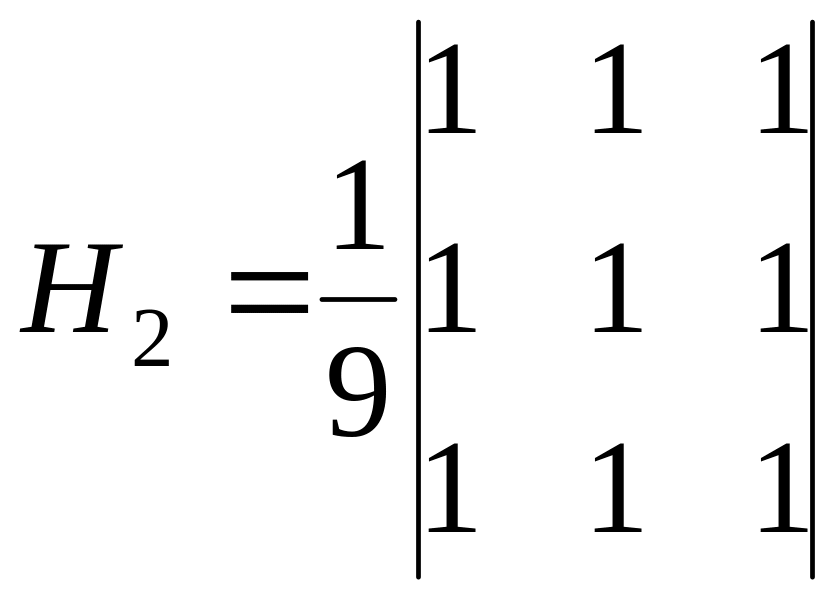
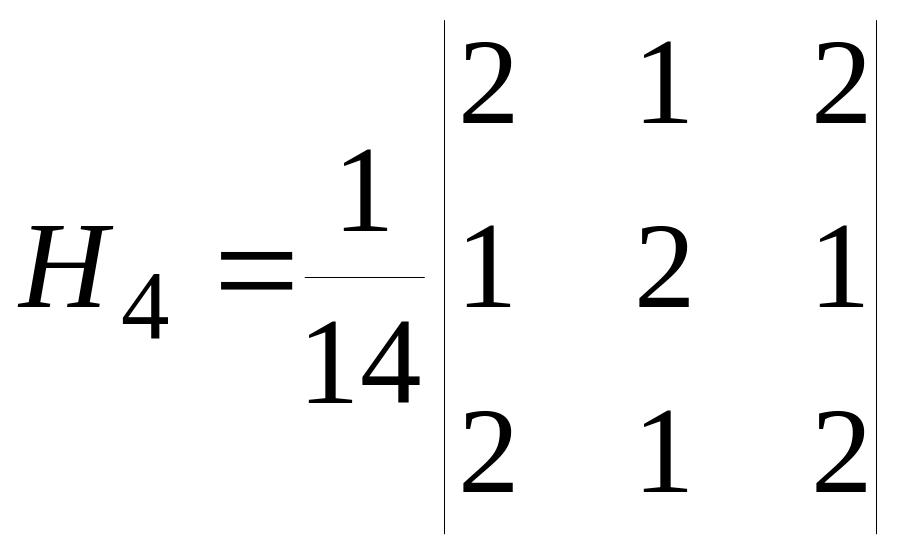
Усереднюючий фільтр використовується у випадку наявності на зображення адитивного білого шуму. Слід зазначити що використання цього фільтру на ряду з видаленням шуму згладжує контури об’єктів.

Наведемо результати використання такого типу фільтрів для покращення якості зображення (див. рис. 1.9). Слід зазначити, що при використанні цього фільтру у випадку наявності імпульсного (зображення на рис зліва знизу) шуму приводить до появи практично білого шуму на зображенні. Взагалі не існує формальних методів за допомогою яких можна визначити, який з фільтрів слід використовувати, для того щоб видалити всі завади. Як правило для конкретного типу зображень з завадами обирають той фільтр, який дає найкращий результат.

Рисунок 1.9 – Використання усереднюючого фільтру (зліва – зображення з завадами, справа – оброблені фільтром)

У випадку наявності імпульсного шуму найкращі результати дає використання медіанної фільтрації.

Медіанний фільтр реалізується наступним чином. Зображення з маски зчитується в одновимірний масив , кількість елементів якого дорівнює . Елементи цього масиву впорядковуються у порядку зростання. Значення яскравості пікселу, наприклад, , що розташований у центрі маски замінюється значенням , тобто медіаною.

Наприклад, якщо , то після впорядкування він буде мати вид , відповідно .

На рис. 1.10 наведено результат застосування медіанного фільтру до зображення з імпульсним шумом.

Рисунок 1.10 – Фільтрація імпульсного шуму медіанним фільтром

Якщо порівняти результати фільтрації цього ж зображення, то можна дійти висновку, застосування медіанного фільтру дає більш якісні результати у порівнянні з усереднюючим фільтром.

Гаусівський фільтр визначається з використанням функції двовимірного розподілу щільності ймовірності Гауса з нульовим середнім значенням

, (1.15)

де – координати, – дисперсія.

На рис. 1.11 наведено графік двовимірної функції Гауса з дисперсією та нульовим середнім значенням.

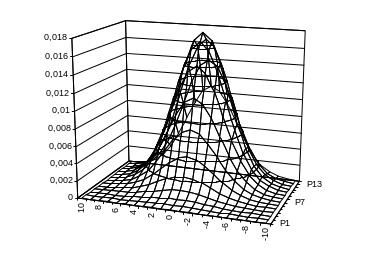Рисунок 1.11 – Двовимірна функція Гауса.

Для того щоб побудувати гаусівський фільтр обирають розмір маски та значення дисперсії. Розглянемо це на прикладах побудови гаусівського фільтра з масками та . Для маски координати її чарунок будуть мати наступні значення

	1 (1)	2 (0)	3 (-1)
1 (1)	1,1	1,0	1,-1
2 (0)	0,1	0,0	0,-1
3 (-1)	-1,1	-1,0	-1,-1

Оберемо та обчислимо значення функції Гауса

Таблиця 1.1 – Значення функції Гауса для маски

	1	0	-1
1	0,05857953	0,09658132	0,05857953
0	0,09658132	0,15923567	0,09658132
-1	0,05857953	0,09658132	0,05857953

На практиці використовуються цілі значення функції Гауса, для цього помножимо кожне значення на 20, тоді отримаємо, що

Аналогічним чином для маски при значенні множника 400 отримаємо

.

Розглянемо результати фільтрації зображень з використанням побудованих гаусівських фільтрів.

а) б) в)

Рисунок 1.12 – Результати обробки вхідного зображення (а) гаусівськими фільтрами з маскою 3×3 – б) та 5×5 – в)

Як видно з наведених рисунків збільшення розміру маски приводить до більшого розмивання границь об’єктів на зображенні.