
- •Принципи побудови систем розпізнавання графічних зображень
- •1.1. Загальні відомості
- •1.2 Перетворення зображень у цифрову форму
- •1.2.1 Дискретизація та квантування зображень
- •1.2.2 Бінарний спосіб подання цифрових зображень в пам’яті еом
- •1.3 Попереднє оброблення зображень
- •1.3.1 Редагування яскравості
- •1.3.2 Фільтрація зображень
- •1.3.3 Бінаризація зображень
- •1.3.2 Способи видалення завад на бінаризованих зображеннях
- •1.4. Мінімізація поворотів поштових відправлень у системах розпізнавання поштових індексів
- •Побудова мінімальної послідовності поворотів конвертів (карток)
- •Побудова мінімальної послідовності поворотів посилок
- •1.5 Пошук та захоплення поштового індексу
- •Контрольні питання
- •Список рекомендованої літератури
- •2. Системи розпізнавання стилізованих цифр
- •2.1. Загальні відомості
- •2.1.1 Характеристика систем оптичного розпізнавання символів
- •2.1.2 Характеристики стилізованих цифр
- •2.2. Виділення і запис ознак стилізованих цифр
- •2.3. Класифікація стилізованих цифр
- •Контрольні питання
- •Список рекомендованої літератури
- •3. Системи розпізнавання нормалізованих цифр
- •3.1. Загальні відомості
- •3.2. Виділення і запис ознак нормалізованих цифр
- •3.3. Класифікація нормалізованих цифр
- •Контрольні питання
- •Список рекомендованої літератури
- •4. Системи розпізнавання штрихових кодів
- •4.1. Загальні відомості
- •4.2. Засоби зчитування штрихових кодів
- •За конструктивним виконанням портативний сканер може являти собою олівець, пістолет або пзз-сканер.
- •4.3. Декодування штрихових кодів
- •Контрольні питання
- •Список рекомендованої літератури
- •5. Адаптація алгоритмів розпізнавання до афінних спотворень графічних зображень
- •5.1. Загальна характеристика афінних спотворень графічних зображень
- •5.2. Визначення параметрів афінних спотворень графічних зображень
- •5.3. Урахування параметрів афінних спотворень в алгоритмах розпізнавання графічних зображень
- •Контрольні питання
- •Список рекомендованої літератури
- •6. Оптимізація показників якості розпізнавання графічних зображень
- •6.1. Показники якості розпізнавання графічних зображень
- •6.2. Застосування критерію мінімального ризику при розпізнаванні графічних зображень рукописних цифр
- •6.3. Приклад застосування критерію мінімального ризику при розпізнаванні графічних зображень
- •Контрольні питання
- •Список рекомендованої літератури
- •7. Організація автоматизованого оброблення поштових відправлень на базі розпізнавальних систем поштового зв’язку
- •7.1. Організація автоматизованого сортування поштових відправлень
- •7.2. Організація автоматизованого обліку і контролю пересилання поштових відправлень
- •7.3. Забезпечення розпізнавання поштових індексів у реальному часі
- •Контрольні питання
- •Список рекомендованої літератури
- •8. Від розпізнавання адреси до розпізнавання поштового відправлення
- •8.1. Розширення можливостей розпізнавання конфігурацій шрифтів від надрукованих до рукописних
- •8.2. Збільшення кількості рядків зчитування та розпізнавання
- •8.3. Перехід від розпізнавання адрес на листах до всіх видів пошти
- •8.4. Перехід від розпізнавання тільки адрес до розпізнавання та інтерпретації всіх зображень, позначок та текстів на поштових відправленнях
- •8.5. Перехід від розпізнавання алфавіту однієї мови до багатомовного
- •8.6. Перехід від розпізнавання на одній сортувальній машині до об’єднаної обчислювальної системи сортувальних центрів
- •8.7 Удосконалення баз даних поштових адрес
- •8.8 Удосконалення систем відеокодування
- •8.9. Нові поштові коди та засоби ідентифікації
- •8.10 Перехід від позначення розпізнаного листа штриховим кодом до запам"ятовування образу листа як його ідентифікатора для подальшої обробки
- •8.11. Слідкування за проходженням поштових відправлень на кожному етапі від приймання до вручення та удосконалення розрахунків
1.2 Перетворення зображень у цифрову форму
Для того
щоб перетворити зображення з аналогової
форми у цифрову необхідно виконати дві
процедури: дискретизацію та квантування.
Нехай зображення описується функцією
![]() ,
де
,
де
![]() – координати у площині зображення, які
мають потужність множини дійсних чисел,
при цьому їх називають неперервними, а
значення
– координати у площині зображення, які
мають потужність множини дійсних чисел,
при цьому їх називають неперервними, а
значення
![]() – характеристика кольору або яскравість
точки зображення з координатами
.
У загальному випадку, дискретизація
полягає у переході від координат
– характеристика кольору або яскравість
точки зображення з координатами
.
У загальному випадку, дискретизація
полягає у переході від координат
![]() ,
які є дійсними числами, до нових координат
,
які є дійсними числами, до нових координат
![]() ,
які є цілими числами. При цьому функція
замінюється множиною значень
,
які є цілими числами. При цьому функція
замінюється множиною значень
![]() ,
які називаються відліками. У свою чергу
квантування полягає у заміні множини
значень
,
яка є множиною дійсних чисел, дискретною
скінченою множиною характеристик
кольору або яскравості дискретного
елементу зображення
,
які називаються відліками. У свою чергу
квантування полягає у заміні множини
значень
,
яка є множиною дійсних чисел, дискретною
скінченою множиною характеристик
кольору або яскравості дискретного
елементу зображення
![]() ,
де
,
де
![]() .
Після виконання процедур дискретизації
та квантування отримують зображення у
цифровій формі. Розглянемо процедури
дискретизації та квантування більш
детально.
.
Після виконання процедур дискретизації
та квантування отримують зображення у
цифровій формі. Розглянемо процедури
дискретизації та квантування більш
детально.
1.2.1 Дискретизація та квантування зображень
Дискретизацію
аналогового зображення можна виконати
різними методами, наприклад, з використанням
інтегральних перетворень. На практиці
використовується періодична дискретизація,
яка полягає у наступному. Обирається
крок дискретизації по кожній з координат:
![]() та
та
![]() .
Далі зображення «розбивається» на
окремі елементи, як це схематично
зображено на рис. 1.4.
.
Далі зображення «розбивається» на
окремі елементи, як це схематично
зображено на рис. 1.4.
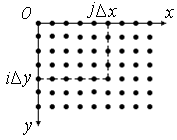 Рисунок
1.4 – Відліки прямокутної періодичної
дискретизації
Рисунок
1.4 – Відліки прямокутної періодичної
дискретизації
Відповідність
між відліками кольору
![]() та функцією
та функцією
![]() визначається рівністю
визначається рівністю
![]() .
.
Решітку, яку отримують у результаті дискретизації називають растром. Елементи растру (відліки) прийнято називати пікселами. Ця назва походить від англійського терміну "pixel", що є скороченням слів picture element – елемент рисунку, зображення.
Від величини кроків дискретизації залежить розподільна здатність дискретизованого зображення, яку прийнято визначати як кількість пікселів в одному дюймі (1 дюйм дорівнює 2,53 см), яку позначають абревіатурою ppi – pixels per inch. Наприкад, розподільна здатність 60 ppi означає що в одному дюймі міститься 60 пікселів. Від розподільної здатності залежить якість відтворення дискретизованого зображення. Проілюструємо це на прикладі дискретизації зображення трикутника за умови що його розміри 1×1 дюйм.
З наведених рисунків слідує, що чим більша розподільна здатність тим менше відмінностей між реальним та дискретизованим зображеннями.
 а) б) в)
а) б) в)
Рисунок 1.5 – Дискретизація з різною розподільною здатністю а) оригінальне зображення; б,в) дискретизовані зображення з розподільними здатностями у 4 та 8 ррі.
Звичайно,
що не можна як завгодно збільшувати
розподільну здатність, тому постає
питання визначення умов щодо вибору
оптимального кроку дискретизації. Ці
умови можна отримати, якщо розглядати
як двовимірний сигнал
![]() з обмеженим частотним спектром:
з обмеженим частотним спектром:
![]() ,
,
![]() .
Тоді, згідно з теоремою Котельникова,
крок дискретизації повинен задовольняти
умовам:
.
Тоді, згідно з теоремою Котельникова,
крок дискретизації повинен задовольняти
умовам:
![]() ,
,
![]() .
Виконання цих умов забезпечує максимальну
якість дискретизованого зображення та
мінімізує помилку відтворення аналогового
зображення з дискретизованого.
.
Виконання цих умов забезпечує максимальну
якість дискретизованого зображення та
мінімізує помилку відтворення аналогового
зображення з дискретизованого.
При
цифровій обробці зображень діапазон
значень характеристик кольору або
яскравості поділяється на ряд дискретних
рівнів. Ця процедура називається
квантуванням. Розглянемо процедуру
квантування на прикладі функції однієї
змінної
![]() .
Квантування цієї функції складається
з наступних кроків. Спочатку множина
її значень, у найпростішому випадку,
розбивається на
.
Квантування цієї функції складається
з наступних кроків. Спочатку множина
її значень, у найпростішому випадку,
розбивається на
![]() діапазонів
діапазонів
![]() ,
,
![]() .
.
Кожному
з цих діапазонів приписується відповідний
рівень квантування
![]() .
Тоді значення функції
.
Тоді значення функції
![]() замінюється на відповідний рівень
квантування
(див. рис. 1.6). При рівномірному квантуванні,
діапазони та рівні визначаються з
використанням співвідношень [1.3]
замінюється на відповідний рівень
квантування
(див. рис. 1.6). При рівномірному квантуванні,
діапазони та рівні визначаються з
використанням співвідношень [1.3]
![]() ,
,
![]() ,
,
![]()
а
середньоквадратична помилка квантування
буде дорівнювати
![]() .
Тобто, як і у випадку дискретизації
якість квантованого зображення залежить
від кроку квантування
.
Тобто, як і у випадку дискретизації
якість квантованого зображення залежить
від кроку квантування
![]() .
.
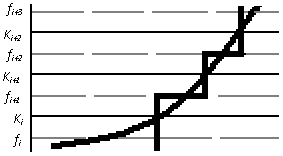 Рисунок
1.6 – Рівні квантування
Рисунок
1.6 – Рівні квантування
З
використанням рівномірного квантування
розроблено графічний формат ВМР. У
цьому форматі використовується адитивна
модель відображення кольрів у ЕОМ. Це
так звана RGB-модель, або простір кольорів
RGB. У цій моделі використовують три
основних кольори: червоний – R, зелений
– G та синій –B. Довільний колір отримують
як суму трьох основних з різними
інтенсивностями. Для відображення
інтенсивності кожного кольору
використовується 256 рівнів квантування.
Це дозволяє використовувати у цифровій
формі для кодування кожного з цих
кольорів один байт. При цьому можна
відобразити
![]() різних відтінків (людина може розрізняти
лише близько 10 млн. відтінків кольору).
різних відтінків (людина може розрізняти
лише близько 10 млн. відтінків кольору).
