Динамика урожайности зерновых культур в хозяйстве

(определение параметров уравнения методом наименьших квадратов)

Год	Урожайность, Ц/га, у,	t	(2	yrt	Vt
А	1	2	3	4	5
1987	13,7	-7	49	-95,9	13,6
1988	12,1	-6	36	-72,6	13,8
1989	14,0	-5	25	-70,0	13.9
1990	13,2	-4	16	-52,8	14,1
1991	15,6	-3	9	-46,8	14,3
1992	15,4	-2	4	-30,8	14,5
1993	14,0	-1	1	-14,0	14,6
1994	17,6	0	0	0	14,8
1995	15,4	1	1	15,4	15.0
1996	10,9	2	4	21,8	15,1
1997	17,5	3	9	52,5	15,3
1998	15,0	4	16	60,0	15,5
1999	18.5	5	25	92.5	15,7
2000	14,2	6	36	85,2	15,8
2001	14,9	7	49	104,3	16,0
Итого	222,0	0	280	48,8 222,0

447

ряда нечетное (л = 15) (табл. 10.11). При этом система уравнений при. И

мет вид

Используя итоги граф 1, 3, 4, определим па­

раметры уравнения прямой

По рассчитанным параметрам запишем уравнение прямой ряда динамики урожайности зерновых культур:

Данное уравнение показывает, что в течение исследуемого перио­да урожайность в хозяйстве увеличивалась в среднем на 0,17 ц/га в год.

Используя приведенное уравнение, рассчитаем для каждого года теооетические значения-

Правильность расчета уровней выравниваемого ряда динамики может быть проверена следующим образом: сумма значений эмпири­ческого ряда должна совпасть с суммой выравненных значений ряда,

Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворитель­ных результатов, так как в рядах динамики содержатся заметные пе­риодические колебания вокруг общей тенденции или наблюдается автокорреляция не в самих уровнях, а в их отклонениях от теорети­ческих значений, полученных по определенным аналитическим фор­мулам. В таких случаях следует использовать гармонический анализ.

Целью данного анализа являются выявление и измерение периоди­ческих колебаний в рядах динамики и автокорреляции в остатках ряда-

Функцию, заданную в каждой точке изучаемогоцннтервала време­ни, можно представить бесконечным рядом синусоидальных и коси-нусоидальных функций. Нахождение конечной суммы уровней с ис'

448

1тьзованием функций косинусов и синусов времени называется гар-

^оническим анализом.

Другими словами, гармонический анализ представляет собой опе-ацию по выражению заданной периодической функции в виде ряда Омоье по гармоникам разных порядков. Каждый член ряда представ­ляет собой слагаемое постоянной величины с функциями косинусов и синусов определенного периода.

В простейшем случае динамика явлений, обладающих периодич­ностью, может быть аппроксимирована синусоидой:

время;

полуамплитуда колебания, т.е. наибольшее и наименьшее отклонения от оси (;

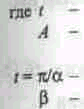
период (длина волны) колебательного движения;

начальная фаза колебания.

При (= 0 получаем у^ = y4sinp.

Аппроксимация динамики экономических явлений рядом Фурье состоит в выборе таких гармонических колебаний, наложение кото­рых друг на друга (сумма) отразит периодические колебания факти­ческих уровней динамического ряда. С помощью ряда Фурье можно представить динамику явлений в виде некоторой функции времени, в которой слагаемые расположены по убыванию периодов:

(10.38)

В этом уравнении величина k определяет гармонику ряда Фурье и может быть взята целым числом (чаще всего от 1 до 4). Параметры Уравнения рассчитываются методом наименьших квадратов.

Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, из которой вычислим па-Р^етры:

449

^ Последовательные значения / обычно определяются от 0 с увеличе.

нием (приростом), равным 2я/п, где п - число уровней ряда динамики.

Для изучения специфического периодического явления - сезон­ности берется п = 12, по числу месяцев в году.

Тогда ряд динамики годового производства можно записать так:

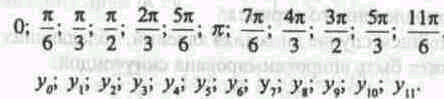
Для определенных в каждом конкретном случае t находят значе­ния синусов и косинусов разных гармоник, которые для удобства рас­полагают в табл. 10.12.

Таблица 10.12

Коэффициент гармонического анализа месячных наблюдений ' для расчета параметров а^ и Ь^

t	COS(	cosit	cos3/	cos4(	siru	sin2(	sin3/	sin4(
0	1	1	1	1	0	0	0	0
я/6	0,866	0.5	0	-0,5	0,5	0,866	1	0,866
я/3	0,5	-0,5	-1	-0.5	0.866	0,866	0	-0,866
я/2	0	-1	0	1	1	0	-1	0
2л/3	-0,5	-0,5	1	-0,5	0,866	-0,866	0	0,866
5п/6	-0,866	0.5	0	-0,5	0,5	-0,866	1	-0,866
я	-1	1	-1	1	0	0	0	0
7п/6	-0,866	0,5	0	-0,5	-0,5	0,866	-1	0,866
4л/3	-0,5	-0.5	1	-0.5	-0,866	0,866	0	-0,866
Зя/2	0	-1	0	1	-1	0	1	0
5я/3	0,5	-0,5	-1	-0.5	-0,866	-0,866	0	0,866
Итс/б	0,866	0.5	0	-0.5	-0,5	-0,866	-1	-0,866

450

Полагая гармоники Л соответственно равными 1,2,3 и т.д., нахо­дим все значения coskt и smkt. Тогда, например, первая гармоника

ряда Фурье примет вид:

здесь:

(10.39)

Ряд Фурье с двумя гармониками:

(10.40

Исчисление параметров ряда Фурье может производиться и дру­гими способами, а также путем использования различных шаблонов.

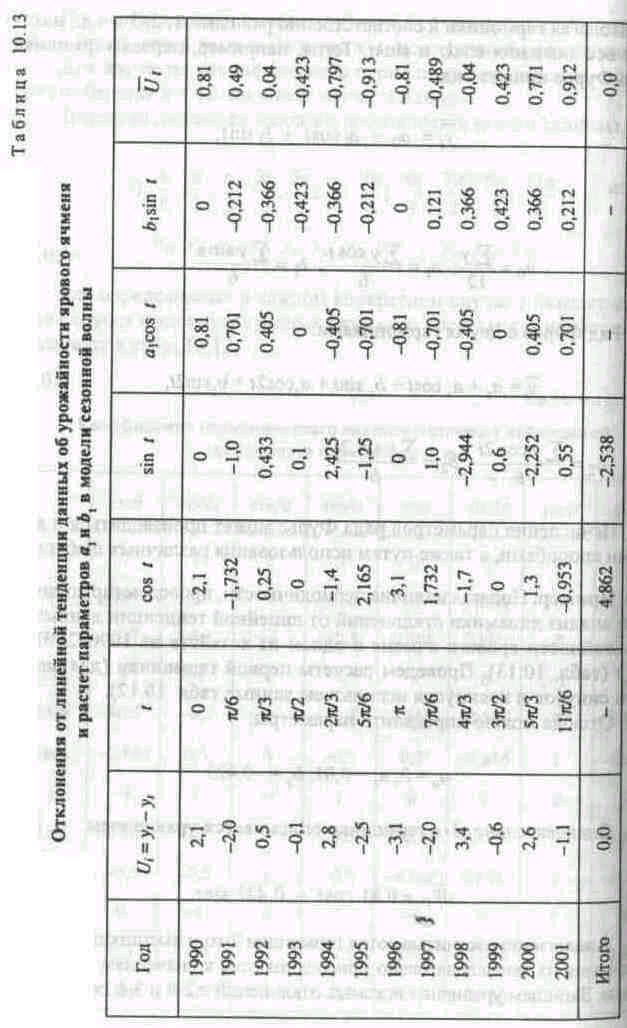
Пример. Полагая наличие периодичности, проведем гармоничес­кий анализ динамики отклонений от линейной тенденции данных об Урожайности ярового ячменя в одном из хозяйств на 1990-2001 гг. (U) (табл. 10.13). Проведем расчеты первой гармоники (для значе­ний синусов и косинусов используем данные табл. 10.12).

Отсюда можно определить параметры:

Следовательно, 1-я гармоника описывается уравнением

Аналогично рассчитываются гармоники 2-го и высших порядков, и ^{здачения} их последовательно присоединяются к значениям 1-й гармо-^вдки- Запишем уравнения искомых отклонений с 2-й и 3-й гармоник.

451

Для 2-й гармоники:

Для 3-й гармоники:

Подставив в уравнение конкретные значения cost, sin, cos2, sin2, cos3(, sin3/, получим выравненные уровни отклонений урожайности ярового ячменя за 1990-2001 гг. Затем, рассчитав остаточные диспер­сии (ст²^ = £(>', -уУ '. п) для трех гармоник, можно сделать вывод, какая гармоника рада Фурье наиболее близка к фактическим уровням рада.