Тема 5.4. Границя функції

5.4.1. Границя функції в точці

Нехай функція визначена в деякому околу точки , крім, можливо, самої точки .

Сформулюємо два, еквівалентних між собою, означення границі функції в точці.

Означення 1. (на «мові послідовностей», або по Гейне). Число А називається границею функції в точці (або при ), якщо для будь-якої послідовності допустимих значень аргументу , ( ), що збігається до (тобто ), послідовність відповідних значень функції , , збігається до числа А.

В цьому випадку пишуть або при . Геометрично значення границі функції : означає, що для всіх точок х, достатньо близьких до точки , відповідні значення функції як завгодно мало відрізняються від числа А.

Означення 2 (на «мові e-d», або по Коші). Число А називається границею функції в точці (або при ), якщо для будь-якого додатного e знайдеться таке додатне число d, що для всіх , які задовольняють нерівність , викону ється нерівність .

Записують . Це означення коротко можна записати так :

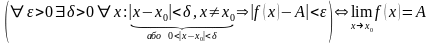
Г еометричне тлумачення границі функції : А= , якщо для будь-кого e- окілу точки А знайдеться такий d- окіл точки , що для всіх з цього d- околу відповідні значення функції ¦(х) лежать в e- околі точки А. Іншими словами, точки графіка функції лежать усередині смуги шириною 2e, обмеженої прямими 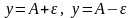(див. рис.110).

Очевидно, що величина d залежить від вибору e, тому пишуть .

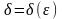Приклад 16.1 Довести, що

○ Візьмемо довільне , знайдемо таке, що для всіх х, задовольняючих нерівності , виконується нерівність 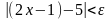, тобто |x-3|< . Узявши d= , бачимо, що для всіх х, задовольняючих нерівності ), виконується нерівність . Отже ○

Приклад 16.2. Довести, що, якщ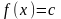о , то .

○ Для можна узяти 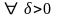. Тоді при 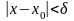, маємо

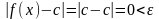. Отже .●

5.4.2.Односторонні границі

У означенні границі функції вважається, що х прямує будь-яким способом : залишаючись меншим, ніж (зліва від ), більшим, ніж (праворуч від ), або коливаючись біля точки .

Бувають випадки, коли спосіб наближення аргументу х до істотно впливає на значення границі функції. Тому вводять поняття односторонніх границь.

Число називається границею функції зліва в точці , якщо для будь-кого число існує число таке, що при , виконується нерівність . Границю зліва записують так : або коротко (позначення Діріхле) (див. рис.111)

Аналогічно визначається границя функції справа, запишемо його за допомогою символів :

Коротко границю справа позначають .

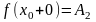Границі функції зліва і справа називаються односторонніми межами . Очевидно, якщо існує, то існують і обидві односторонні границі, причому .

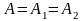Справедливо і зворотне твердження : якщо існують обидві границ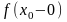і і і вони рівні, то існує границя і

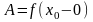
Якщо ж , то не існує.

5.4.3. Границя функції при х®¥

Нехай функція визначена на проміжку . Число А називається границею функції f(x) при , якщо для будь-якого додатного числа e існує таке число 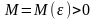, що при всіх х, задовольняючих нерівності |x|>M виконується нерівність . Коротко це означення можна записати так :

Я кщо 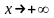, то пишуть , якщо то 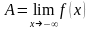. Геометричне значення цього означення таке : для , що при 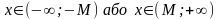х відповідні значення функції потрапляють в e-окіл точки А, тобто точки графіка лежать в смузі шириною 2e, обмеженої прямими (см.рис.112).