Тема 5.2. Функція
5.1.1. Поняття функції
Одним з основних математичних понять є поняття функції. Поняття функції пов'язано зі встановленням залежності ( зв'язки) між елементами двох множин.
Нехай дано дві
не порожні множини
і
.
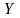Відповідність
,
яка кожному елементу
ставить один і лише
один елемент
називається
функцією і
записується
,
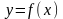або
.
Говорять ще, що функція
відображає
множину
на множину
.
Рис. 98
Наприклад,
відповідності
і
,
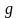зображені на рис. 98 а
і б, є функціями, а на
рис. 98 в і
г –
ні. У випадку в –
не кожному елементу
відповідає елемент
.
У разі г
не дотримується умова однозначності.
Множина
називається
областю визначення
функції
і позначається
.
Множина всіх
називається
множиною значень
функції
і позначається
.
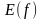5.2.2. Числові функції. Графік функції. Способи задання функцій
Нехай задана функція .
Якщо
елементами множин Х
і
У
є
дійсні числа (тобто
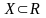і
),
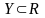то функцію
називають
числовою
функцією.
Надалі вивчатимемо(як правило) числові
функції, називатимемо їх просто функціями
і записуватимемо
.
Змінна
називається
при цьому аргументом
або
незалежною змінною, а
–
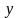функцією
або
залежною змінною (від
).
Щодо самих величин
і
говорять,
що вони знаходяться у функціональній
залежності.
Іноді функціональну залежність у
від
х
пишуть
у вигляді
,
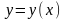не вводячи нової букви
(
)
для позначення залежності.
Власне
значення
функції
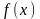при
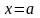записують
так :
.
Наприклад, якщо
,
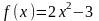то
.
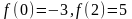Рис. 99
Графіком
функції
називається
підмножина точок площини
,
для кожної з яких
є
значенням аргументу, а
–
відповідному значенням функції.
Наприклад,
графіком функції
=
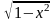є верхнє півколо радіусу
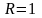з
центром в О(0;
0) (див. рис. 99).
Щоб задати функцію , необхідно вказати правило, що дозволяє, знаючи , знаходити відповідне значення .
Найбільш часто зустрічаються три способи завдання функції : аналітичний, табличний, графічний.
Аналітичний спосіб : функція задається у вигляді однієї або декількох формул або рівнянь.
Наприклад :
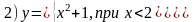
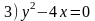
Якщо
область визначення функції
не
вказана, то передбачається, що вона
співпадає з множиною
всіх значень аргументу, при яких
відповідна формула має сенс. Так, областю
визначення функції
=2
є відрізок [-1; 1].
Аналітичний спосіб завдання функції є самим зручним, оскільки до нього прикладені методи математичного аналізу, що дозволяють повністю досліджувати функцію
Графічний спосіб : задається графік функції.
Часто графіки викреслюються автоматично самописними приладами або зображаються на екрані дисплея. Значення функції , відповідні тим або іншим значенням аргументу , безпосередньо знаходяться з цього графіка.
Перевага графічного способу є його наочність, недоліком – його неточність.
Табличний спосіб : функція задається таблицею ряду значень аргументу і відповідних значень функції. Наприклад, відомі таблиці значень тригонометричних функцій, логарифмічні таблиці.
На практиці часто доводиться користуватися таблицями значень функцій, отриманих досвідченим шляхом або в результаті спостережень.