
- •Гидрогазодинамика Учебное пособие
- •Воронеж 2005
- •Введение
- •1. Основы гидростатики
- •1.1. Физические свойства жидкостей
- •1.2. Основные понятия и уравнения гидростатики
- •2. Основные понятия и уравнения гидродинамики
- •2.1. Определения кинематики жидкости. Неразрывность
- •2.2. Уравнения движения идеальной жидкости Эйлера
- •2.3. Уравнение Бернули
- •2.4. Примеры применения уравнения Бернулли
- •2.5. Уравнение количества движения
- •3 Потери напора и гидравлические сопротивления расчет трубопроводов
- •3.1 Режимы движения вязкой жидкости. Потери напора по длине трубы
- •3.2. Местные сопротивления и расчет трубопроводов
- •3.3. Гидравлический удар в трубах
- •4. Движение газа без скачков уплотнения
- •4.1 Исходные уравнения
- •4.2. Примеры применения теории одноразмерного изоэнтропического течения газа
- •4.3. Одномерное течение газа с трением
- •4.4 . Возмущения в дозвуковом и сверхзвуковом потоках. Характеристики
- •5. Скачки уплотнения
- •5.1. Прямой скачек
- •5.2. Косые скачки уплотнения
- •5.3. Взаимодействие сверхзвукового потока с ограничивающими поверхностями
- •6 Основы динамики идеальной несжимаемой жидкости
- •6.1. Кинематический анализ движения жидкости
- •6.2. Функция тока и потенциал скорости
- •6.3. Вихревое движение жидкости
- •6.4. Обтекание тел идеальной жидкостью
- •7.3. Подобие потоков при действии различных сил
- •8.1. Общие понятия и дифференциальные уравнения пограничного слоя
- •8.2. Интегральные соотношения и расчет пограничного слоя
- •8.3. Отрыв пограничного слоя и сопротивление при отрывном обтекании
- •9. Течения газа в диффузорах и эжекторах
- •9.1 Диффузоры
- •9.2. Эжекторы
- •Библиографический список
- •394026 Воронеж, Московский просп., 14
5. Скачки уплотнения
5.1. Прямой скачек
Возникновение скачка. Конечное по величине изменение давления можно рассматривать как сумму следующих друг за другом малых возмущений. С конечным возмущением сжатия в капельной жидкости мы познакомились в § 3.3, посвященном гидравлическому удару.
Р ис.35
ис.35
Рассмотрим теперь процессы распространения конечных возмущений в газе.
Пусть в трубе с неподвижным газом (рис. 35) начинает ускоренно перемещаться поршень и по достижении скорости w продолжает двигаться равномерно. В отличие от вывода формулы для скорости звука (§ 3.3) считаем скорость w не малой по сравнению с а. Впереди поршня распространяется волна сжатия С, которая отделяет неподвижный невозмущенный газ от сжатого поршнем. На рис. 35 область волны сжатия покрыта точками.
Основание, или «подножие», волны сжатия (О на рис. 35) движется вправо со скоростью, равной скорости звука в покоящемся газе а0. Гребень волны сжатия (Г на рис. 35) движется быстрее: здесь больше скорость распространения возмущений, так как при сжатии газ нагревается. Кроме того, к этой скорости здесь добавляется скорость движения газа вместе с поршнем w. В результате гребень догоняет основание, и в последовательные моменты времени t1, t2, t3 возрастание давления в волне сжатия становится все более резким. Наконец, на некотором расстоянии от поршня возникает ударная волна – прерывное изменение давления, в котором параметры газа меняются очень резко на расстоянии порядка длины свободного пробега молекулы, т. е. при нормальных условиях — порядка микронов. Ударная волна движется в газе со скоростью w1, превышающей скорость звука.
Сзади поршня по трубе распространяется волна разрежения Р. Скорость распространения гребня волны разрежения равна а0, тогда как скорость основания меньше — здесь сказывается охлаждение газа и его течение за поршнем. Поэтому волна разрежения делается все более пологой; ударные волны возможны только в волнах уплотнения.
Прерывное изменение параметров газа и скорости течения наблюдается также и при обтекании неподвижного тела сверхзвуковым потоком. Если, например, обтекаемое тело имеет спереди затупленную форму, то торможение газа в лобовой части приводит к появлению здесь области дозвуковых скоростей. Волны повышения давления от тела распространяются в этой области дозвуковых скоростей и навстречу потоку, но на сравнительно небольшое расстояние — до скачка уплотнения, расположенного перед телом. В скачке уплотнения сверхзвуковая скорость потока прерывно переводится в дозвуковую. До перехода через скачок сверхзвуковой поток остается невозмущенным — волны давления от обтекаемого тела распространяются со скоростью звука, а скорость потока ее превышает.
Если система координат связывается с областью прерывного сжатия газа (или с обтекаемым телом, относительно которого она неподвижна), то эта область прерывного изменения параметров газа называется скачком уплотнения. Сквозь него протекает газ, имея сверхзвуковую скорость w1 на входе и w2= w1- w на выходе. Температура, давление и плотность в скачке мгновенно возрастают.
Если система координат связана с неподвижным газом, в котором распространяется со сверхзвуковой скоростью область прерывного сжатия, то эта область называется ударной волной. Физические процессы, происходящие в скачке уплотнения и в ударной волне, одинаковы, поэтому иногда оба эти названия применяют для одного и того же явления (например, скачок уплотнения перед затупленной передней частью тела называют «головной ударной волной», [Л. 7]).
Изменение параметров газа в прямом скачке. Прерывное уплотнение сжатия, которое расположено по нормали к вектору скорости (рис. 36), называется прямым скачком уплотнения.
Рассмотрим движение газа через прямой скачок уплотнения. Исходные уравнения:
Уравнение неразрывности (4.9), имеющее в данном случае вид:
![]() (5.1)
(5.1)
2. Уравнение количества движения (2.22), приводящееся к виду:
![]() (5.2)
(5.2)
3. Уравнение энергии в форме:
![]() (5.3)
(5.3)
Если заданы три величины, например w1, р1, ρ1, то из приведенных уравнений могут быть определены три остальные: w2, p2, ρ2.
Приведем основные результаты совместного решения исходных уравнений.

Рис. 36![]() .
.
Выразим
отсюда отношение
![]() (перед
скачком) и
(перед
скачком) и
![]() (после скачка):
(после скачка):
![]() ;
;
![]() .
.
Если теперь разделить уравнение (5.2) на (5.1):
![]()
и
подставить полученное
ранее значение
![]() ,
получим
,
получим
![]() .
.
Разделив
на w1-w2
(деление возможно, так как на скачке
скорость изменяется,
![]() )
и выполнив алгебраические преобразования,
получим, что скорости w1
и w2
связаны между собой соотношением
)
и выполнив алгебраические преобразования,
получим, что скорости w1
и w2
связаны между собой соотношением
![]() ,
или
,
или
![]() .
(5.4)
.
(5.4)
Следовательно, в прямом скачке уплотнения сверхзвуковой поток (λ > 1) всегда переходит в дозвуковой (λ < 1).
Определим
разность скоростей
![]() (для
ударной волны
это – скорость, которую газ имеет за
ударной волной; на
рис. 35 — скорость движения газа вместе
с поршнем). Из соотношения
(5.4)
(для
ударной волны
это – скорость, которую газ имеет за
ударной волной; на
рис. 35 — скорость движения газа вместе
с поршнем). Из соотношения
(5.4)
 .
(5.4)
.
(5.4)
Возрастание давления в скачке р2 – р1 получим, подставляя разность скоростей w1 – w2 в уравнение (5.2):
![]() .
(5.5)
.
(5.5)
Возрастание
плотности ρ2
– ρ1
найдем из уравнения неразрывности и
соотношения (5.4); так как
![]() ,
то
,
то
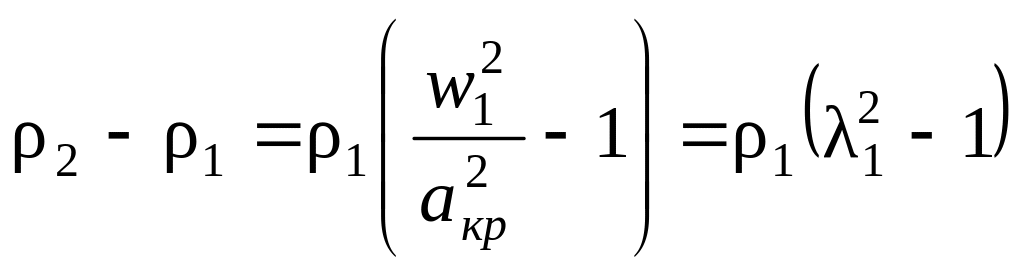 (5.6)
(5.6)
Рис. 37 з
равенств (5.4) — (5.6) следует, что изменение
параметров на скачке тем резче,
чем больше λ1,
т. е. его интенсивность усиливается с
ростом сверхзвуковой скорости на
входе в скачок. На рис. 37 представлена
зависимость величин
з
равенств (5.4) — (5.6) следует, что изменение
параметров на скачке тем резче,
чем больше λ1,
т. е. его интенсивность усиливается с
ростом сверхзвуковой скорости на
входе в скачок. На рис. 37 представлена
зависимость величин
![]() и
и
![]() от
безразмерного отношения скоростей λ
для воздуха (k
= 1,4); по оси абсцисс отложены также
соответствующие значения чисел М.
от
безразмерного отношения скоростей λ
для воздуха (k
= 1,4); по оси абсцисс отложены также
соответствующие значения чисел М.
Ударная адиабата. Рост энтропии и потеря давления в прямом скачке.. Безразмерная скорость газа λ –
величина ограниченная.
Действительно,
![]() ,
,
или, с использованием соотношений (4. 15) и (4. 16),
![]()
(для воздуха λmax = 2,449; это значение λ соответствует М = ∞). Поэтому возрастание плотности в скачке уплотнения (формула 5.6) оказывается ограниченным:
![]() .
.
Для воздуха (k = 1,4) возможно максимальное уплотнение в скачке в 6 раз.
В то же время известно, что при обратимом (изоэнтропическом) адиабатном сжатии
 .
.
т. е. при возрастании давления плотность возрастает неограниченно.
Связь между давлением и плотностью в скачке может быть получена из совместного решения уравнений (5.5) и (5.6). Она называется ударной адиабатой или адиабатой Гюгонио (приводится без вывода):
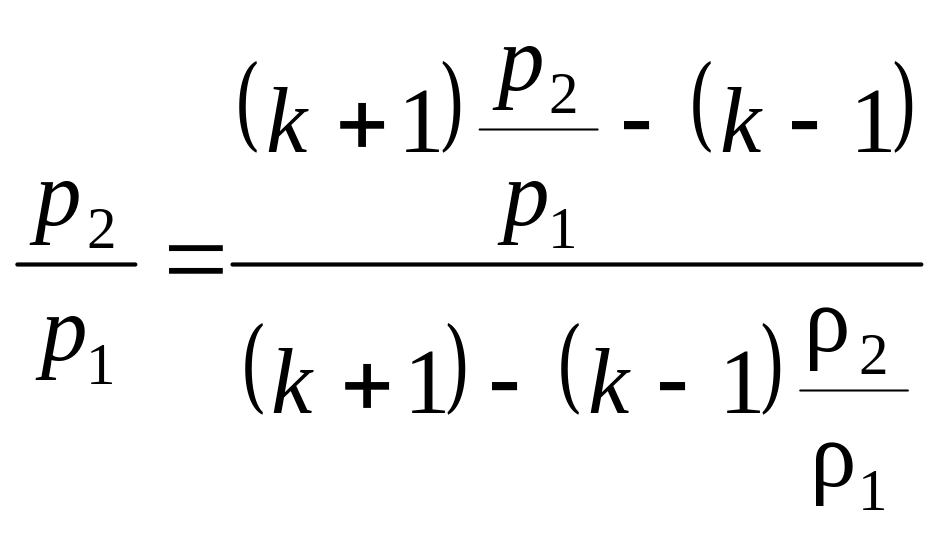 .
(5.7)
.
(5.7)
На рис. 38 представлено изменение давления при изменении плотности воздуха для изоэнтропического сжатия [зависимость (6.2), кривая 1] и для сжатия в скачке уплотнения [уравнение (5.7), кривая 2]. Асимптота адиабаты Гюгонио показана пунктиром.
Рис. 38 ак
известно из термодинамики, при теплообмене
между телами, входящими в систему,
энтропия системы возрастает. При течении
газа без скачков теплообмен между
частицами пренебрежимо мал, движение
изоэнтропическое. В то же время процесс
сжатия газа в скачке уплотнения — не
изоэнтропический,
энтропия в скачке нарастает. Это
происходит вследствие передачи тепла
от уплотненного и нагретого объема газа
к невозмущенному газу процессами
теплопроводности; температура в скачке
резко меняется на очень малом расстоянии
толщины ударной волны, порядка микронов.
ак
известно из термодинамики, при теплообмене
между телами, входящими в систему,
энтропия системы возрастает. При течении
газа без скачков теплообмен между
частицами пренебрежимо мал, движение
изоэнтропическое. В то же время процесс
сжатия газа в скачке уплотнения — не
изоэнтропический,
энтропия в скачке нарастает. Это
происходит вследствие передачи тепла
от уплотненного и нагретого объема газа
к невозмущенному газу процессами
теплопроводности; температура в скачке
резко меняется на очень малом расстоянии
толщины ударной волны, порядка микронов.
Доля кинетической энергии частицы газа единичной массы, равная
![]() [дж/кг],
[дж/кг],
переходит в тепловую энергию. Однако при расширении газа от давления р2 снова до давления р1 эта тепловая энергия не полностью преобразуется снова в кинетическую. Потери механической энергии характеризуются коэффициентом восстановления давления σ, равным отношению давлений торможения за скачком и до скачка:
![]() .
(5.8)
.
(5.8)
Коэффициент восстановления давления приходится вводить, например, при измерении скорости сверхзвукового потока трубкой Пито (см. рис. 43, б): в скачке уплотнения, который появляется перед трубкой, происходят потери давления. Отметим, что температура торможения, характеризующая полную энергию газа, одинакова для изоэнтропического и скачкового сжатия. Действительно, при переходе через скачок уменьшается механическая энергия частиц газа и возрастает их внутренняя (тепловая) энергия. Полная же энергия, мерой которой является температура торможения, остается неизменной.
П араметры
газа за прямым скачком и величины
коэффициента восстановления давления
приводятся в таблицах прямых скачков
облегчающих решение задач. Такие
таблицы даны.
араметры
газа за прямым скачком и величины
коэффициента восстановления давления
приводятся в таблицах прямых скачков
облегчающих решение задач. Такие
таблицы даны.
Рис. 39
