4.2. Примеры применения теории одноразмерного изоэнтропического течения газа
Связь скорости газа с течением потока. Сопло Лаваля. Выясним зависимость скорости течения от площади поперечного сечения потока. Для газа уравнение неразрывности (2.6), или уравнение постоянства массового расхода при установившемся течении имеет вид:
const.
(4.9)
Логарифмируя и дифференцируя это равенство, получим
,
(4.9а)
откуда
.
(4.9б)
Из уравнения энергии в дифференциальной форме (4.7) имеем
,
что даёт после подстановки в уравнение (4.9б)
.
Поскольку
согласно формуле (3.12а)
,
имеем
.
(4.10)
Из уравнения (4.10) следует, что изменение скорости dw при измене
Рис. 23
ии
сечения dF
происходит по-разному для дозвукового
и сверхзвукового течения. В дозвуковом
потоке (w<a,
M<1,
рис. 23, а)
знаки dw
и dF
в (4.10) противоположны: уменьшение сечения
в конфузорном
канале приводит к возрастанию скорости,
и, наоборот, в диффузорном
канале скорость по потоку уменьшается.
При сверхзвуковом
течении (w<a,
M<1,
рис. 23, б) в
конфузорном канале поток замедляется,
в диффузорном – ускоряется.
Чтобы пояснить полученные результаты, которые для сверхзвукового течения кажутся неожиданными, сопоставим уравнения (4.10) и (4.9б). Имеем
.
(4.11)
Поскольку левая часть равенства (4.11) всегда положительна, ясно, что знаки dρ и dw всегда противоположны: рост скорости приводит к уменьшению плотности. Но при дозвуковом течении (M2<1) скорость изменяется более быстро, чем плотность:
.
При сверхзвуковом течении, наоборот более быстро уменьшается плотность:
.
Для получения сверхзвуковых скоростей газа в технике используется сопло Лаваля (1889, рис. 24), принцип действия которого ясен из приведённых рассуждений. В дозвуковом потоке, поступающем в суживающуюся часть сопла Лаваля, скорость увеличивается. Если в наименьшем сечении сопла не достигается скорость, равная скорости звука, то в расширяющейся части происходит её уменьшение; скорость по длине сопла изменяется по кривой I на рис. 24. Если перепад давления достаточно велик, чтобы в наименьшем сечении скорость течения сравнялась со скоростью звука, то при дальнейшем расширении поток переходит в сверхзвуковой, скорость его изменяется по кривой II.
Сопло Лаваля имеет широкое применение, являясь составной частью реактивных двигателей, сопловых аппаратов некоторых турбин (в которых рабочие лопатки обтекаются сверхзвуковым потоком), сверхзвуковых аэродинамических труб и т.д. Более полная теория сопла учитывает влияние трения на стенках и волновых явлений на выходе потока.
Параметры
изоэнтропического торможения газа.
При торможении газа его кинетическая
энергия переходит в потенциальную, при
этом давление, плотность и температура
возрастают.
Рис. 24
Применим уравнение (4.8в) к сечениям струйки «на бесконечности», т. е. там, где на поток не сказывается искажающее влияние обтекаемого тела, и в точке торможения:
.
Как
и следовало ожидать, мы получили частный
случай уравнения (4.8г).
Разделив последнее выражение на
,
получаем
.
Принимая
во внимание, что
,
где М∞
– число М
для невозмущённого потока, и что согласно
формуле (4.5а)
,
имеем
.
(4.12)
П
овышение
температуры газа у поверхности тела,
обтекаемого при больших числах М,
называется аэродинамическим
нагревом.
Отметим, что термометр, помещённый в
поток газа, показывает температуру,
очень близкую к температуре торможения.
Используя зависимости (4.3), связывающие температуру адиабатного процесса с давлением и плотностью, получим
;
.
(4.13)
Рис. 25
Расчёт по формулам (4.12) и (4.13) показывает, что при М=0,2 (для воздуха при 15ºС это соответствует скорости 68 м/сек) сжимаемость газа приводит к поправкам в плотности торможения на 2%, в давлении и температуре – порядка 1%. Ввиду малости этих поправок ими пренебрегают, считая газ при малых скоростях несжимаемой жидкостью. В задачах, не требующих высокой точности решения, можно считать газ несжимаемым и при больших числах М (порядка 0,3).
Выражения (4.12) и (4.13) являются, по сути дела, ещё одной формой записи уравнения (4.8).
Истечение газа из резервуара. Максимальная и критическая скорости. Исследуем истечение газа из резервуара, где он находился под давлением p0 , в среду с давлением p.
Применяя к сечениям струйки газа в резервуаре, где скорость близка к нулю, и в сжатом сечении уравнение энергии в форме (4.8), имеем
,
откуда
.
Выражая
отношение
через отношение
с помощью уравнения
адиабаты (4.2) и используя уравнение
состояния (4.1), получим формулу
Сен-Венана и Ванцеля
(1839) для скорости адиабатного истечения
газа:
.
(4.14)
Е
сли
газ вытекает в пустоту (p=0),
то достигается максимальная
скорость истечения:
.
(4.15)
В частности, если в пустоту вытекает воздух при температуре 15ºС, то wmax =760 м/сек.
Рис. 26
,
(4.16)
называют критическим давлением, скорость истечения достигает максимума, она сравнивается с местной скоростью звука, устанавливается критическая скорость потока aкр. Плотность и температура газа при этом также достигает критических значений, определяемых формулами:
;
.
(4.16а)
Величину критической скорости легко определить из уравнения энергии в форме (4.8в) или (4.8г), если принять w=a=aкр:
.
(4.17)
В частности, для воздуха, имеющего температуру 15ºС, aкр=0,91 a0= 310 м/сек. При дальнейшем уменьшении противодавления p скорость истечения остаётся неизменной и равной aкр (рис. 26).
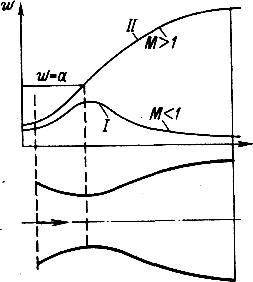
Постоянство скорости (и расхода) при p<pкр можно объяснить следующим образом. Представим себе (рис.27), что газ вытекает из резервуара I в вакуумную камеру II через трубу, давление в которой регулируется краном К. При p>pкр скорость w<aкр и при открытии крана волны разрежения от него, распространяясь навстречу струе, соответственно увеличивают скорость истечения. Если достигнута звуковая скорость истечения, то волны разрежения от крана уже не могут распространяться навстречу струе и понижение давления p не меняет скорость течения w=aкр.
Рис. 27
Величина
критической скорости aкр
остаётся постоянной вдоль струйки.
Поэтому удобно измерять скорость течения
в долях этой величины; так вводится
безразмерная скорость газа, иногда
называемая коэффициентом скорости:
.
(4.18)
В знаменателе безразмерной скорости – величина постоянная вдоль струйки, тогда как в выражении для числа М (4.6) – знаменатель переменный. При w=aкр имеем λ=М=1. Связь между этими величинами очевидна из отношения
.
Используя уравнение энергии в форме (4.8г), получим
.
Газодинамические функции для воздуха (k = 1,4)
,
,
Таблица 4
λ |
τ |
π |
ε |
q |
Μ |
0,00 |
1,0000 |
1,0000 |
1,0000 |
0,0000 |
0,0000 |
0,05 |
0,9996 |
0,9986 |
0,9990 |
0,0788 |
0,0457 |
0,10 |
0,9983 |
0,9942 |
0,9959 |
0,1571 |
0,0914 |
0,15 |
0,9963 |
0,9870 |
0,9907 |
0,2344 |
0,1372 |
0 20 |
0,9933 |
0,9768 |
0,9834 |
0,3102 |
0,1830 |
0,25 |
0,9896 |
0,9640 |
0,9742 |
0,3842 |
0,2290 |
0.30 |
0,9850 |
0,9485 |
0,9630 |
0,4557 |
0,2760 |
0,35 |
0,9796 |
0,9303 |
0,9497 |
0,5243 |
0,3228 |
0,40 |
0,9733 |
0,9097 |
0,9346 |
0,5897 |
0,3701 |
0,45 |
0,9663 |
0,8868 |
0,9178 |
0,6515 |
0,4179 |
0,50 |
0,9583 |
0,8616 |
0,8991 |
0,7091 |
0,4663 . |
0,55 |
0,9496 |
0,8344 |
0,8787 |
0,7623 |
0,5152 |
0,60 |
0,9400 |
0,8053 |
0,8567 |
0,8109 |
0,5649 |
0,65 |
0,9296 |
0,7745 |
0,8332 |
0,8543 |
0,6154 |
0,70 |
0,9183 |
0,7422 |
0,8082 |
0,8924 |
0,6668 |
0,75 |
0,9063 |
0,7086 |
0,7819 |
0,9250 |
0,7192 |
0,80 |
0,8933 |
0,6738 |
0,7543 |
0,9518 |
0,7727 |
0,85 |
0,8796 |
0,6382 |
0,7256 |
0,9729 |
0,8274 |
0,90 |
0,8650 |
0,6019 |
0,6959 |
0,9879 |
0,8833 |
0,95 |
0,8496 |
0,5653 |
0,6653 |
0,9970 |
0,9409 |
1,00 |
0,8333 |
0,5283 |
0,6340 |
1,0000 |
1,0000 |
1,05 |
0,8163 |
0,4913 |
0,6019 |
0,9969 |
1,0609 |
1,10 |
0,7983 |
0,4546 |
0,5694 |
0,9880 |
1,1239 |
1,15 |
0,7796 |
0,4184 |
0,5366 |
0,9735 |
1,1890 |
1,20 |
0,7600 |
0,3827 |
0,5035 |
0,9531 |
1,2566 |
1,25 |
0,7396 |
0,3479 |
0,4704 |
0,9275 |
1,3268 |
1,30 |
0,7183 |
0,3142 |
0,4374 |
0,8969 |
1,4002 |
1,35 |
0,6962 |
0,2816 |
0,4045 |
0,8614 |
1,4769 |
1,40 |
0,6733 |
0,2505 |
0,3720 |
0,8216 |
0,5575 |
1;45 |
0,6496 |
0,2209 |
003401 |
0,7778 |
1 ,6423 |
1,50 |
0,2250 |
0,1930 |
0,3088 |
0,3707 |
1,3721 |
1,55 |
0,5996 |
0,1669 |
0,2784 |
0,6807 |
1 ,8273 |
1,60 |
0,5733 |
0,1427 |
0,2489 |
0,6282 |
1,9290 |
1,65 |
0,5463 |
0,1205 |
0,2205 |
0,5740 |
2,0380 |
1,70 |
0,5183 |
0,1003 |
0,1934 |
0,5187 |
2,1555 |
1,75 |
0,4896 |
0,0821 |
0,1677 |
0,4630 |
2,2831 |
1,80 |
0,4600 |
0,0660 |
0,1435 |
0,4075 |
2,4227 |
1,85 |
0,4296 |
0,0520 |
0,1210 |
0,3530 |
2,5766 |
1,90 |
0,3983 |
0,0399 |
0, 1002 |
0,3002 |
2,7481 |
1,95 |
0,3662 |
0,0297 |
0,0812 |
0,2497 |
2,9414 |
2,00 |
0,3333 |
0,0214 |
0,0642 |
0,2024 |
3,1622 |
2,05 |
0,2996 |
0,0147 |
0,0491 |
0,1588 |
3,4190 |
2,10 |
0,2650 |
0,0096 |
0,0361 |
0,1198 |
3,7240 |
2,15 |
0,2296 |
0,0058 |
0,0253 |
0,0857 |
4,0961 |
2,20 |
0,1933 |
0,0032 |
0,0164 |
0,0570 |
4,5674 |
2,25 |
0,1563 |
0,00151 |
0,00966 |
0,0343 |
5,1958 |
2,35 |
0,1183 |
0,00057 |
0,00482 |
0,0175 |
6,1033 |
2,40 |
0,0796 |
0,00014 |
0,00170 |
0,0063 |
7,6053 |
2,449 |
0,0400 |
0,128·10-4 |
0,00032 |
0,0012 |
10,957 |
|
0 |
0 |
0 |
0 |
∞ |
Переходя в формулах для параметров торможения газа (4.12) и (4.13) от числа М к λ, получим соотношения:
;
;
.
(4.19)
Формулы (4.19) дают изменение параметров газа вдоль струйки в зависимости от скорости. Они носят название газодинамических функций. Их численные значения для различных k и λ (или М) сведены в таблицы и графики газодинамических функций. В частности, величины газодинамических функций для воздуха (k=1,4) даны в табл. 4. В таблицах газодинамических функций даются также значения приведённого расхода q(λ), где
,
(4.20)
т. е. q – это отношение удельного расхода массы газа в произвольном сечении струйки к расходу в критическом сечении( здесь Fкр – площадь критического сечения сопла). Использование таблиц газодинамических функций существенно облегчает расчёты.