1.4. Кристалографічні позначення

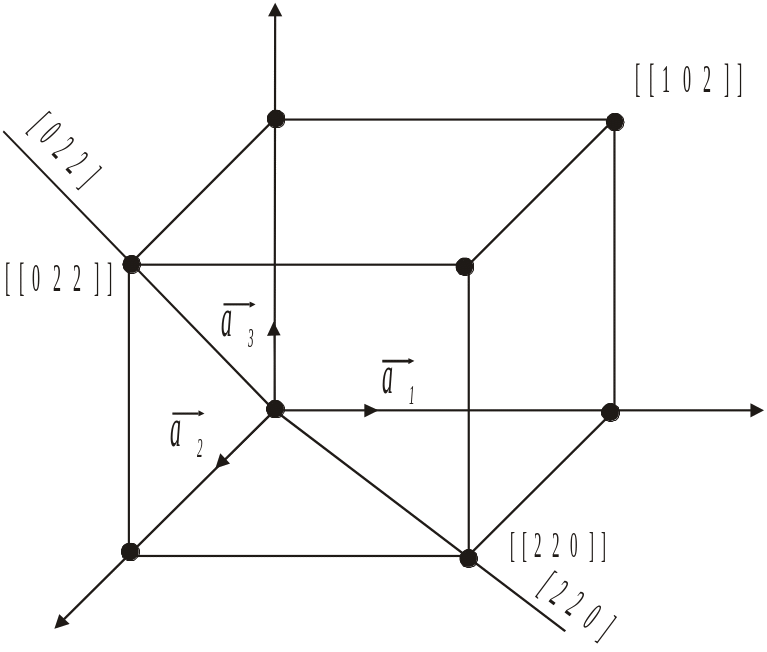
Внаслідок кристалічної будови твердих тіл більшість з них анізотропні, тобто їх фізичні властивості залежать від напрямку їх спостереження у кристалі. З метою визначення положення точки, прямої або площини у кристалічній ґратці зручно вибрати систему координат, вісі якої паралельні векторам основних трансляцій. Положення довільного вузла у такій системі координат (відносно початку координат, суміщеного з положенням одного з вузлів) визначається впорядкованою трійкою чисел l, m та n – коефіцієнтів вектора (1.1) переміщення з початку координат до цього вузла. Такі трійки мають назву індексів вузлів і позначається символом [[lmn]]. У випадку складних ґраток числа l, m, n не обов’язково цілі.

Рис. 1.9. До пояснення змісту символів вузлів і напрямків УВАГА! Бажано би зменшити, але забезпечити виразність позначень векторів

Для визначення напрямків у кристалі вибирають пряму, що проходить через початок координат та перший з вузлів, через який вона проходить. Оскільки початок координат – спільна точка усіх прямих, що визначають довільний напрямок, а відрізняються вони тільки вузлом з ненульовими індексами [[l m n]], то індекси цього вузла однозначно визначають напрямок. У цьому випадку впорядковані трійки цілих чисел l, m, n називаються індексами напрямку і позначаються символом [l m n] (рис 1.9). Якщо індекси вибраного вузла [[l m n]] – не цілі, то їх приводять до цілих значень, які й приймають за індекси напрямку. Наприклад, у ГЦК ґратці перший вузол у напрямку діагоналі основи грані має координати (0, 1/2, 1/2). Відповідно, індекси напрямку цієї діагоналі – [011].

Орієнтація площин у кристалі також задається за допомогою індексів – впорядкованих трійок цілих чисел (lmn), що називаються індексами Міллера. Відомо, що рівняння площини, яка відтинає по осях координат відрізки довжиною p, q, r має вигляд:

(рівняння у відрізках). Приводячи ліву частину до спільного знаменника та позбавившись від нього, можемо записати його у вигляді загального рівняння площини

lx + my + nz = D, (1.4)

де D – найменше спільне кратне чисел p, q, r, а l, m та n – цілі числа. Наприклад, якщо площина відтинає на осях координат відрізки 4, 6 та 8 (довжин векторів , , ) , то її рівняння має вигляд

x/4+y/6+z/8=1

або

6x + 4y + 3z = 24,

звідки h = 6, k = 4, l = 3, а індекси Міллера цієї площини – (643).

1.5. Обернена ґратка

Рівняння (1.4) можна інтерпретувати двома способами залежно від того, який набір (x, y, z) чи (l, m, n) вважати змінними величинами. Зазвичай змінними величинами вважаються x, y і z – координати точок простору, положення яких визначається радіус-вектором (будемо називати його -простором). Тоді набір чисел (lmn) (індекси Міллера) – являє собою координати вектора, нормального до площини, яка проходить через точку (x, y, z). При фіксованих l, m і n рівняння (1.4) описує площину, отже (x, y, z) – координати множини точок, які лежать на цій площині.

З іншого боку у рівняння (1.4) набори чисел (x, y, z) та (l, m, n) входять симетрично, а тому перший набір можна вважати фіксованими коефіцієнтами. Тоді величини l, m і n будуть визначати координати (l, m, n) точок деякого іншого (не ) простору. Такий простір називається оберненим, або -простором. Тоді, аналогічно до того як точки (x = l, y = m, z = n) є вузлами [[lmn]] ґратки у -просторі, набір чисел (l, m, n) визначає вузли ґратки у оберненому просторі (оберненої ґратки) з індексами [[lmn]].

Обернена ґратка також володіє трансляційною симетрією, її вектор трансляції

,

де – основні вектори трансляції оберненої ґратки, а l, m і n – довільні цілі числа. Можна показати, що основні вектори трансляції прямої та оберненої ґраток пов’язані між собою співвідношеннями

, , , (1.5)

де – об’єм елементарної комірки прямої ґратки.

Величини x, y, z визначають у -просторі відстані, а тому вимірюються у одиницях довжини (м, см і т.д.). Тоді, як видно з (1.5), вектори -простору вимірюються у одиницях, обернених до одиниць довжини – м^-1, см^-1 і т.п. У таких одиницях вимірюється хвильовий вектор , модуль якого k = 2π/λ (λ – довжина хвилі). Це пояснює назви “обернений простір”, “ -простір”.

Поняття, що використовуються для опису кристалічних ґраток у -просторі – елементарна і примітивна комірка, трансляційна, точкова та просторова симетрії і т.п., – використовуються і для оберненої ґратки. Зокрема, правила побудови комірки Вігнера – Зейтца для оберненої ґратки є такими ж, як і для ґратки у -просторі. Внаслідок історичних причин комірка Вігнера – Зейтца оберненої ґратки називається першою зоною Бріллюена (у подальшому – зоною Бріллюена). Отже зона Бріллюена являє собою многогранник у -просторі, обмежений системою площин

, (1.6)

де – радіус-вектор точок, що лежать на площинах-межах зони Бріллюена, – вектор трансляції оберненої ґратки.