1.2. Трансляційна симетрія кристалів. Кристалічна ґратка

Найважливішою особливістю речовини, що знаходиться в твердому стані є те, що переважна більшість твердих тіл, утворених природним шляхом або в лабораторних умовах, має майже ідеальну геометричну форму. Наприклад, це природні коштовні камені, лід, мінерали, деякі органічні сполуки. Такі тверді тіла прийнято називати кристалами, а стан в якому вони знаходяться – кристалічним станом. Правильна геометрична форма кристалів надавала їм певних важливих властивостей, зокрема оптичних: велика кількість їх є прозорою, мають гарне забарвлення. Після певної обробки, яка полягає у виправленні недоліків, пов’язаних з випадковими відхиленнями від правильної геометричної форми, кристали мають привабливий вигляд і використовуються з давніх часів у якості коштовних прикрас. Завдяки високій твердості і правильній геометричній формі, що характеризується наявністю чітких граней, кристали широко використовуються в техніці у процесах різання, шліфування, свердління і т. п.

Ще в XVII ст. вчені дійшли висновку, що правильна геометрична форма кристалів викликана тим, що вони утворюються шляхом впорядкованого розміщення у просторі одного й того ж структурного елемента, такої собі цеглинки – при вирощуванні кристалу в ідеальних умовах форма його залишається незмінною, так ніби до нього приєднуються нові елементарні утворення (цеглинки). Сучасні уявлення про природу речовини дозволяють стверджувати, що її структурними елементами є молекули. Правильність уявлень про впорядковане розташування їх у кристалі експериментально доведена рентгенографічними дослідами Лауе (1912 р.).

З геометричної точки зору впорядковане розташування структурних елементів у кристалі можна описати за допомогою операції трансляції (переміщення). На рис. 1.2 показано впорядковані множини точок, одержаних шляхом трансляції точки О (початку координат) на:

• а) відрізки la (l = 0, ±1, ±2, ±3) вздовж осі ОХ;

• б) довільний з векторів (l, m = 0, ±1, ±2) на площині XОY;

• в) довільний з векторів

, (1.1)

(тут l = 0, 1, 2, 3; m = 0, 1, 2; n = 0, 1, 2) у тривимірному просторі.

Рис. 1.2. Фрагменти одно- (a), дво- (б) та тривимірної (в) ґраток

УВАГА! Відсутні позначення a, б, в біля рисунків: до того ж різний формат літер і невиразний символ вектора (стрілки)

Аналогічно можна побудувати нескінченну множину впорядкованих (на прямій, на площині або у тривимірному просторі) точок, надаючи числам m, n і p довільних цілих значень та вибираючи у якості , , трійку лінійно незалежних векторів. Впорядкована таким чином множина точок називається кристалічною ґраткою, вектор (1.1) – вектором трансляції, , , – основними векторами трансляції, а їх модулі – періодами ґратки або періодами трансляції. Оскільки множина {m, n, p} нескінчена, то кристалічна ґратка, за означенням, необмежена, а тому у якості точки О може бути вибрана довільна з них. Кристалічна ґратка, побудована шляхом паралельного переміщення довільної з точок за напрямками векторів трансляції, називається трансляційною, або ґраткою Браве.

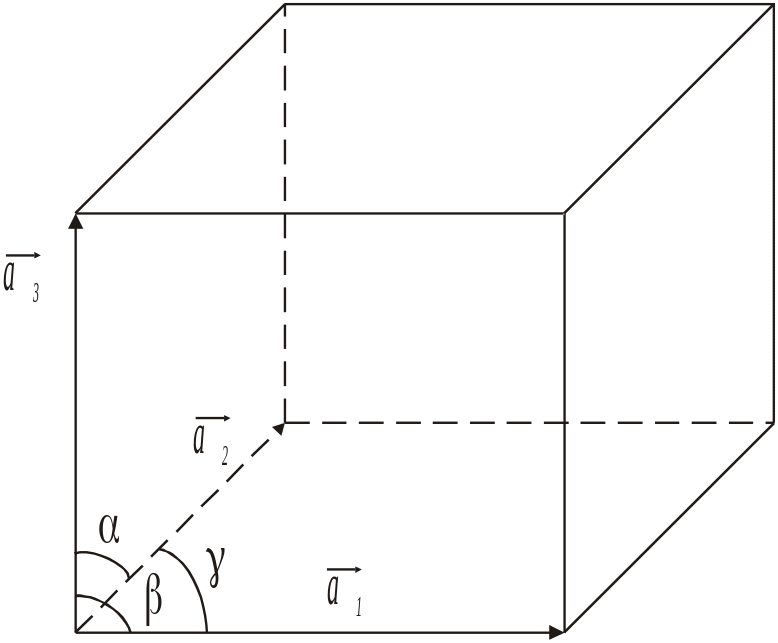
Паралелепіпед, побудований на основних векторах трансляції , , , називається елементарною коміркою кристалічної ґратки (рис. 1.3). Очевидно кристалічна ґратка складається з нескінченої кількості елементарних комірок однакової форми та об’єму

. (1.2)

Рис. 1.3. Елементарна комірка кристалічної ґратки УВАГА! Рисунок зменшити, товщина ліній має бути однакова, символ вектора має бути виразніший.

Отже, ґратку Браве можна побу-

дувати також шляхом трансляцій елементарної комірки. Вона може розглядатись як впорядкована множина еквівалентних точок – вершин елементарних комірок (їх називають вузлами кристалічної ґратки).

Для побудови кристалічної ґратки необхідно задати трійку векторів , , або шість скалярних величин: три ребра a₁, a₂, a₃ елементарної комірки і три кута α, β, γ, між ними (рис. 1.3). Набір цих величин визначає вигляд і розмір елементарної комірки, а тому він є характеристикою ґратки.

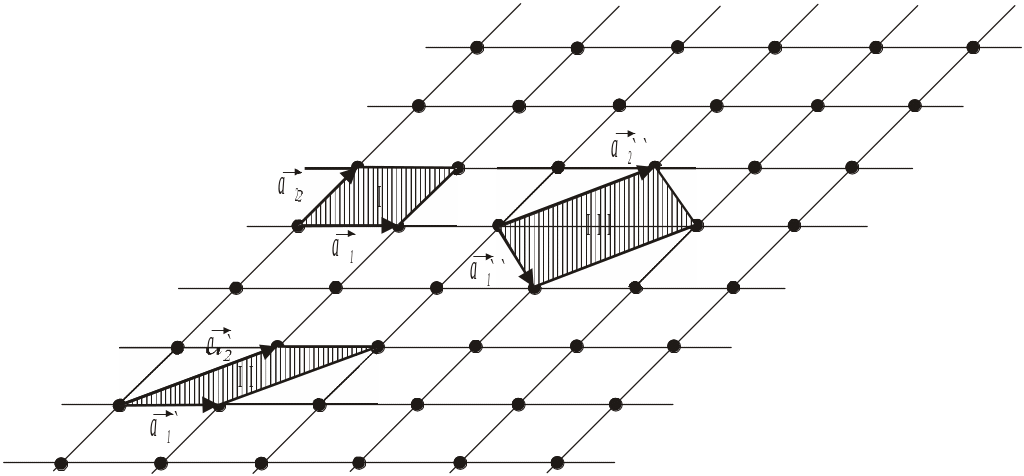
Вибір елементарної комірки є неоднозначним. На рис. 1.4 показано для простоти плоску кристалічну ґратку, для побудови якої можна вибрати, наприклад, одну з трьох елементарних комірок – І, ІІ або ІІІ. Комірки І та ІІ містять по одному атому, їх “об’єм” (насправді йдеться про площу, оскільки розглядається не просторова, а плоска, двовимірна ґратка) однаковий. Комірка ІІІ містить два атоми і має вдвічі більший об’єм. Проте трансляцією кожної з них можна побудувати одну й ту саму кристалічну ґратку. Аналогічна неоднозначність існує й у випадку просторових, тривимірних ґраток.

Рис. 1.4. Можливі варіанти вибору елементарних комірок УВАГА! Рисунок зменшити, символ вектора має бути виразніший.

Якщо елементарна комірка вибрана так, що за допомогою операції трансляції на вектор (1.1) з цілочисельними коефіцієнтами можна з вибраної точки кристалічної ґратки попасти в довільну іншу, еквівалентну їй, точку, то така елементарна комірка називається примітивною. Так, елементарні комірки І і ІІ є примітивними, а ІІІ не є такою: щоби попасти з вершини комірки ІІІ у її центр необхідно здійснити трансляцію з дробовими коефіцієнтами. Очевидно, примітивна комірка є елементарною коміркою мінімального об’єму.

Факт впорядкованості розташування структурних елементів кристалів дозволяє стверджувати про наявність у них трансляційної симетрії – однієї з властивостей кристалічної ґратки, яка полягає у тому, що одночасне переміщення усіх її точок на довільний з векторів трансляції (1.1) не змінює просторового положення ґратки. При цьому кристалічна ґратка називається простою (або примітивною) якщо примітивній комірці належить один атом, у іншому випадку – складною. Складні ґратки мають іноді спеціальні назви, залежно від розміщення атомів у елементарній комірці. Розрізняють такі типи ґраток: а) прості – атоми розташовані у вершинах паралелепіпеда – елементарної комірки; б) базоцентровані – у вершинах та центрах верхньої і нижньої основ; в) об’ємноцентровані – у вершинах та у центрі елементарної комірки; г) гранецентровані – у вершинах та центрах усіх граней (рис. 1.5).

Рис. 1.5. Елементарні комірки простої (a), базо- (б), об’ємно- (в) та гранецентрованої (г) ґраток УВАГА! Замінити літери над (краще б під) рисунками і забезпечити однакову товщину ліній.

У загальному ви-

падку елементарна комірка у формі паралелепіпеда не володіє усіма елементами симетрії кристалічної ґратки. Наприклад, примітивна комірка гексагональної ґратки, що складається з множини прямих шестигранних призм, у вершинах яких розташовані атоми одного сорту, не володіє симетрією правильного шестикутника.

Проте примітивну комірку можна вибрати так, щоби вона володіла повною симетрією ґратки Браве. Наприклад, такими властивостями володіє комірка Вігнера – Зейтца. За означенням, комірка Вігнера – Зейтца з центром у деякій точці ґратки являє собою область простору, розташовану ближче до цієї точки, ніж до будь-якої іншої точки ґратки. Для її побудови необхідно:

1. виділити довільний вузол кристалічної ґратки;

2. провести від нього відрізки до найближчих сусідніх вузлів;

3. через середини відрізків провести площини, перпендикулярні до них;

4. сполучити вибраний вузол з наступними (по відстані) сусідніми вузлами ґратки;

5. перейти до виконання п.3.

Послідовність операцій, описаних у пунктах 3 – 5, виконувати до тих пір, поки побудовані площини, перетинаючись одна з одною, не утворять замкнену поверхню, що обмежує многогранник якнайменшого об’єму у центрі якого міститься вибраний вузол. Побудований таким чином многогранник є коміркою Вігнера – Зейтца. Трансляцією однієї з таких комірок на усі можливі вектори (1.1) можна побудувати ґратку.

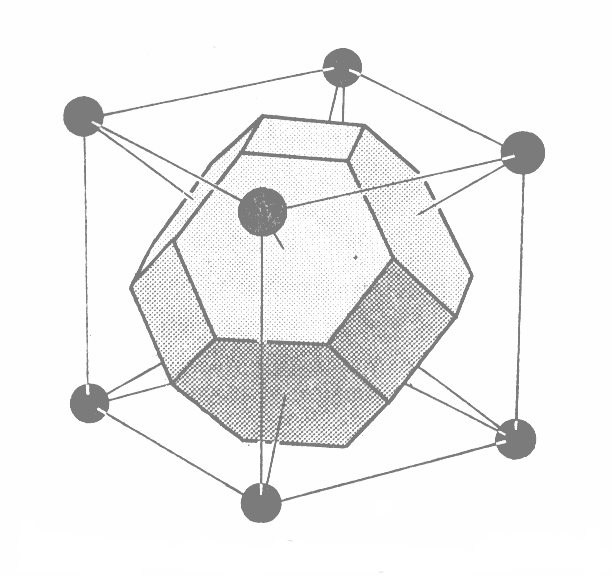
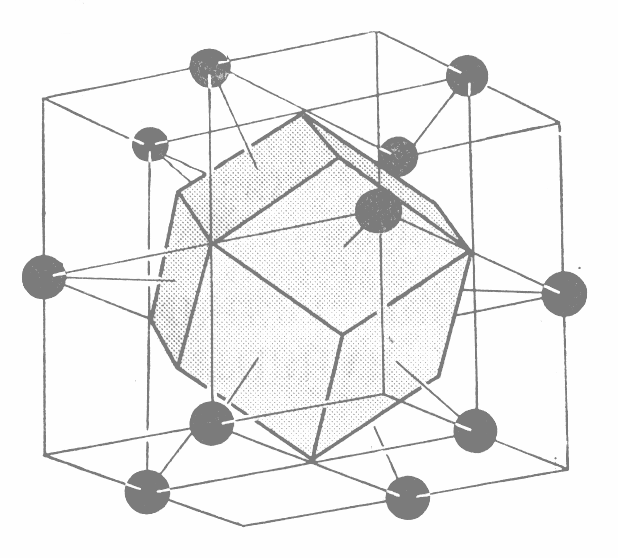
Безпосередньою побудовою можна переконатись, що комірка Вігнера – Зейтца плоскої квадратної ґратки має форму квадрата; плоскої гексагональної базоцентрованої – правильного шестикутника; простої кубічної – куба. Проте у ґраток інших типів форма комірки Вігнера – Зейтца може бути значно складнішою. Наприклад, у випадку об’ємноцентрованої кубічної ґратки вона являє собою зрізаний октаедр – чотирнадцятигранник, що має своїми гранями вісім правильних шестикутників та шість квадратів (рис. 1.6).

а)	б)
Рис. 1.6. Комірка Вігнера-Зейтца (заштрихована) об’ємно- (а) та гранецентрованої (б) кубічної ґраток

З означення комірки Вігнера – Зейтца випливає, що площини її граней визначаються пере-тином сфер рівних радіусів з центрами у сусідніх вузлах ґратки Браве. Координати точок перетину цих сфер знаходяться з розв’язку рівняння

, (1.3)

де – радіус-вектори точок перетину. Його вважають рівнянням площин граней комірки Вігнера – Зейтца, оскільки для будь-якої з граней серед множини векторів трансляції знайдеться такий, що координати довільної точки цієї грані задовольнять рівняння (1.3). Цей факт є проявом періодичності функцій, що характеризують розподіл вузлів ґратки Браве.

Не в усіх існуючих кристалах просторове розміщення їх структурних елементів можна описати за допомогою ґратки Браве. Трансляцією жодного вузла неможливо побудувати, наприклад, кристалічні структури, показані на рис. 1.7. Їх будову можна уявити у вигляді двох вставлених одна в одну ґраток Браве, зміщених на вектор , який називається базисним. У загальному випадку кількість базисних векторів може бути довільною, проте зазвичай вибирають якомога меншу їх кількість, необхідну для побудови даної ґратки.

Рис. 1.7. Приклади складної одновимірної (a) та двовимірної (б) ґраток УВАГА! Бажано би зменшити, але забезпечити виразність позначень векторів та вставити номери рисунків (a та б)

Ґратку загального

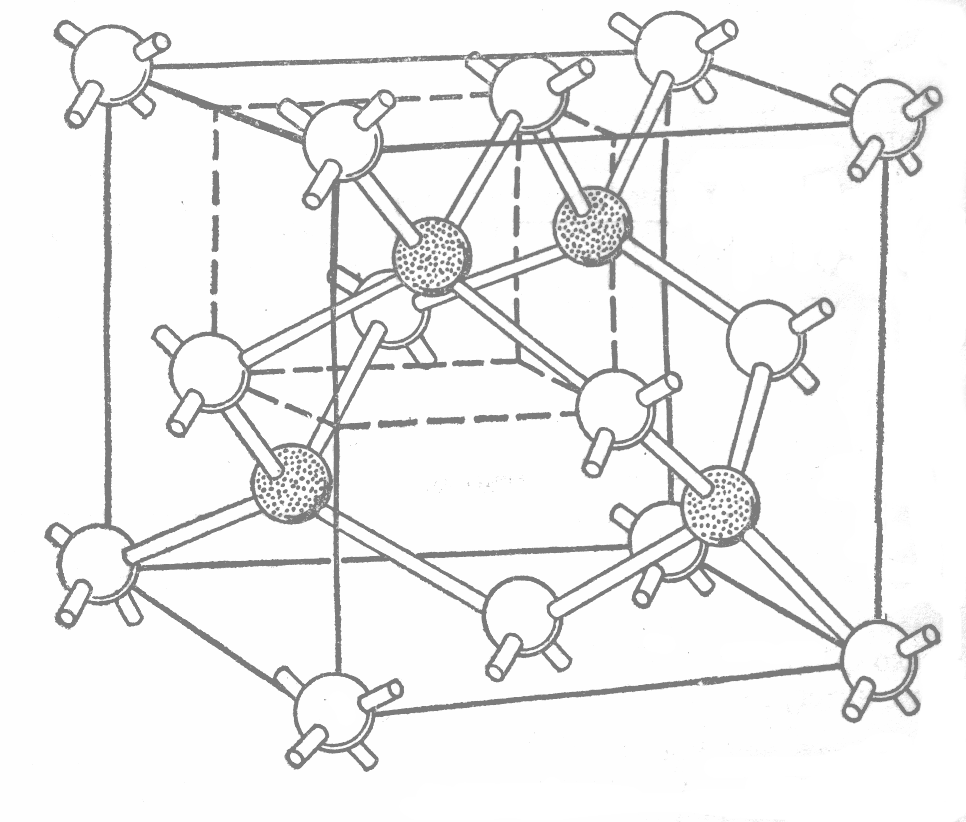
типу називають ґраткою з базисом; її можна одержати за допомогою основних трансляцій , , , тільки транслювати необхідно не вузол, а базис, що визначається сукупністю базисних векторів , , ... . На рис. 1.8 показані приклади тривимірних кристалічних ґраток з базисом: структури алмазу та цинкової обманки, що являють собою пари гранецентрованих кубічних (ГЦК) ґраток, зміщених на 1/4 довжини просторової діагоналі. У випадку алмазу обидві ґратки складаються з атомів одного елемента (вуглецю), а у цинкової обманки (ZnS) – різних (Zn та S). Кожен атом у такій ґратці оточений чотирма найближчими сусідніми атомами (того ж типу у ґратці алмазу, іншого – у цинкової обманки), розміщеними у вершинах тетраедра.

Рис. 1.8. Фрагменти кристалічних ґраток алмазу і цинкової обманки (у випадку алмазу заштриховані і не заштриховані атоми – одного сорту)

За даними рентгеноструктурного аналізу біль-

шість чистих металів характеризуються ґратками з кубічною або гексагональною елементарними комірками. Наприклад, одновалентні метали Li, Na, K, Rb, Cs, двовалентний Ва, перехідні метали (у тому числі α-, β- і δ-модифікації заліза) кристалізуються у структуру з ґраткою у вигляді об’ємноцентрованого куба (ОЦК); метали Cu, Ag, Au, Al, Pb, Pt, Ni та ін. – гранецентрованого куба (ГЦК). Кристали берилію, магнію, цинку, кадмію, ряд сполук важких металів, наприклад CdI₂, мають складну гексагональну ґратку (два атоми у елементарній комірці, , , α = 120˚_, β = γ = 90˚) з базисом (базисний вектор (2a/3, a/3, c/2)).