Задача 2.8 При заданій графічно спектральній щільності середньої потужності (рис.2.9) визначити кореляційну функцію стаціонарного випадкового процесу.

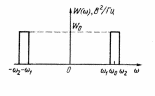
Рисунок 2.9— Графік кореляційної функції (до задачі 2.8)

Розв`язування:

Кореляційна функція по заданій спектральній щільності визначається з виразу:

де,

Графік представлений на рис.2.10.

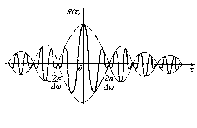
Рисунок 2.10— Графік кореляційної функції (до задачі 2.8)

2.3 Завдання для самостійної роботи

Задача 2.9 Визначити кореляційну функцію сигналу, спектральна щільність якого

Відповідь: .

Задача 2.10 Визначити кореляційну функцію експоненційного імпульсу .

Відповідь:

Задача 2.11 Визначити кореляційну функцію та інтервал кореляції коливання

Відповідь:

Задача 2.12 Визначити взаємні кореляційні функції:

1. двох експоненціальних імпульсів ;

2. довільного сигналу x(t) та дельта-функції ;

3. експоненціального і прямокутного 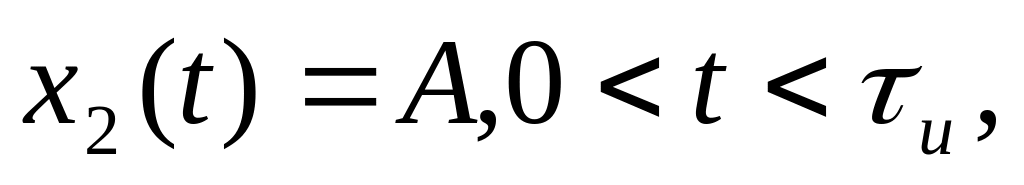імпульсів. Побудувати залежність 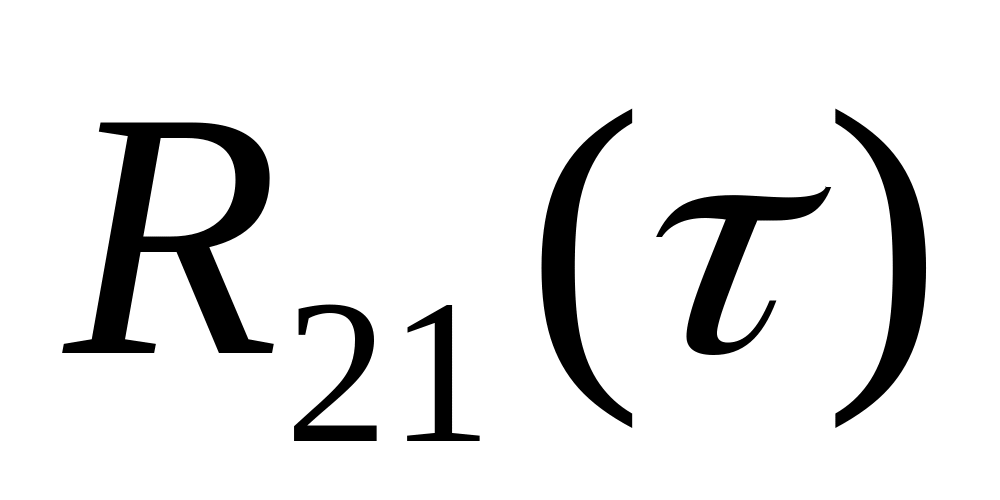при значеннях параметрів А=1 В, .

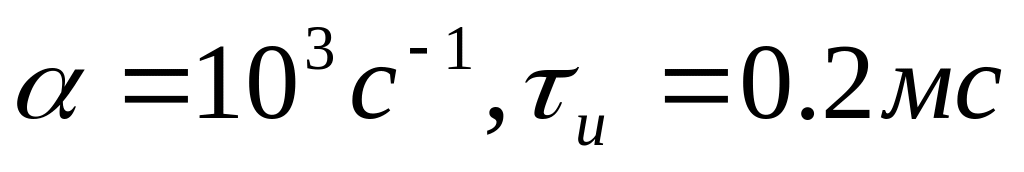Відповідь: Взаємні кореляційні функції:

1. 

2. ;

3. 

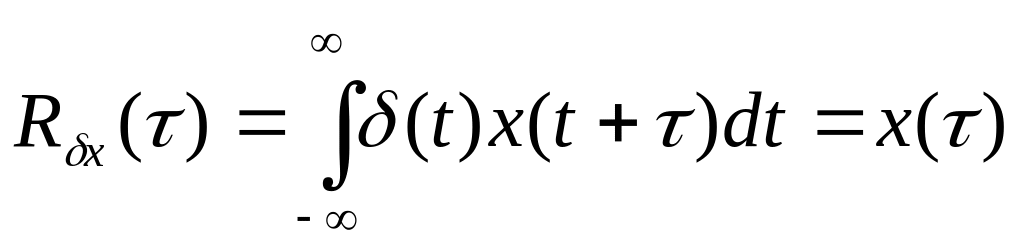На рис. 2.11 зображена залежність при заданих параметрах.

Рисунок 2.11 – Графік взаємної кореляційної функції (до задачі 2.12)

Задача 2.13 Визначити кореляційну функцію і дисперсію стаціонарного випадкового процесу, який володіє спектральною щільністю середньої потужності

Відповідь:

або

2.4 Запитання для самоконтролю

1. Охарактеризуйте суть, алгоритм розрахунку і призначення автоковаріаційної і автокореляційної функцій.

2. Охарактеризуйте суть, алгоритм розрахунку і призначення взаємної кореляційної і взаємної коваріаційної функцій.

3. Здійсніть порівняльний аналіз автокореляційної і автоковаріаційної функцій і зв’язок між ними.

4. Здійсніть порівняльний аналіз автокореляційних і взаємних кореляційних функцій.

5. Які особливості обчислення кореляційних функцій для періодичних, обмежених в часі і випадкових процесів?

6. Охарактеризуйте основні властивості автокореляційної функції.

7. Викладіть суть нормування автокореляційної функції і його практичне застосування.

8. Що таке дисперсія, середнє значення квадрату процесу і який їх зв’язок з кореляційною функцією?

ПРАКТИЧНЕ ЗАНЯТТЯ №3

Розрахунок коефіцієнтів ряду фур’є при апроксимації періодичних сигналів

Мета і завдання заняття: Засвоїти суть, призначення і види записування ряду Фур’є, а також алгоритми розрахунку коефіцієнтів ряду Фур’є при дослідженні інформаційних сигналів. Набути практичних навиків розрахунку аналітичними методами коефіцієнтів ряду Фур’є.

Тривалість заняття— 2 год.

3.1 Основні теоретичні відомості

Найпростішим видом періодичних процесів з погляду їх аналізу є гармонічні процеси. До гармонічних належить синусоїдальний процес, поведінка якого за часом математично виражається такою формулою:

,

де — миттєве значення в момент ; — кругова частота, рад/с; — циклічна частота, Гц; — початковий фазовий кут, рад; — амплітуда гармонічного процесу.

Інтервал часу, на якому відбувається одне повне коливання або цикл гармонічного процесу, називається періодом , а число циклів за одиницю часу— частотою . Частота і період пов’язані співвідношенням:

.

При практичному аналізі гармонічних процесів фазовий кут часто не конкретизується, так як його значення не впливає на кореляційні або спектральні характеристики сигналу. В цьому разі:

.

Рівняння (3.3) графічно можна зобразити або у вигляді залежності миттєвого значення від часу, або у вигляді залежності амплітуди від частоти (частотного спектра) (рис. 3.1).

а)

б)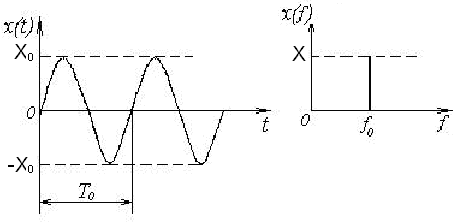

а-графік гармонічного процесу

б-графік спектра гармонічного процесу

Рисунок 3.1— Реалізація і спектр гармонічного процесу

Зазначимо, що частотний спектр, зображений на рис.3.1, складається з єдиної амплітуди, розташованої на певній частоті, і цим відрізняється від спектрів, які задають неперервну залежність амплітуди від частоти. Такі спектри називаються дискретними або лінійчастими.

Відомо багато прикладів фізичних явищ, які на практиці наближено описуються гармонічними процесами. Прикладом можуть бути напруга на виході електричного генератора або механічні коливання незбалансованого обертового вантажу.

Періодичні процеси, що математично описуються функцією часу, яка точно повторює свої значення через одинакові проміжки часу, тобто

, =1,2,3,...,

належать до полігармонічних процесів.

Як і у випадку гармонічних поцесів, проміжок часу, протягом якого відбувається одне повне коливання, називається періодом . Число циклів за одиницю часу називається фундаментальною частотою . Гармонічні процеси— це окремий випадок полігармонічних поцесів при .

Полігармонічні процеси розкладаються в ряд Фур’є у вигляді суми гармонік за формулою:

,

,

де

,

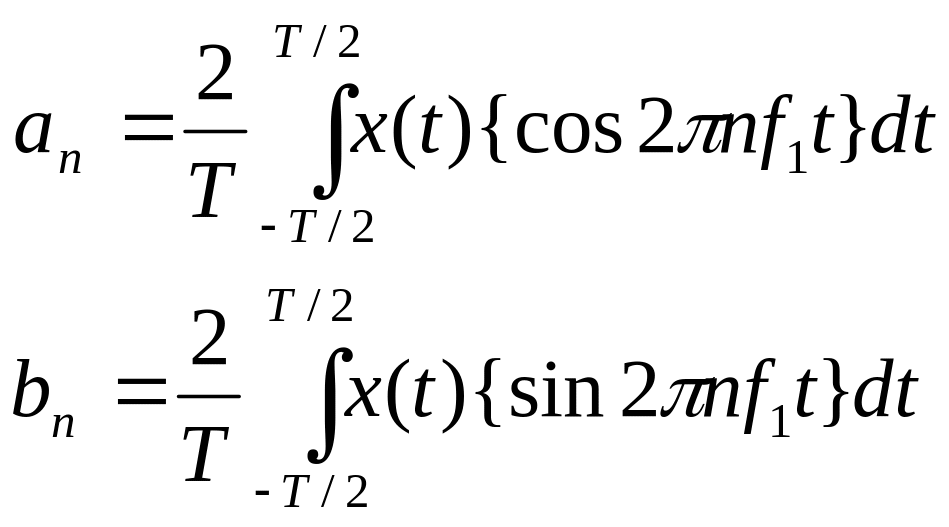
Коефіцієнти , , у формулах (3.5) – (3.8) називаються коефіцієнтами ряду Фур’є, а число відповідає порядковому номеру гармоніки і набуває значень 1, 2,..., 1/ .

Форма (3.5) ряду називається тригонометричною, яка є найбільш поширеним зображенням ряду Фур’є. Практичного застосування набула також амплітудно-фазова форма, яка побудована на підставі того, що вираз можна записати як . Тоді формула (3.5) набуде вигляду:

,

де

(3.10)

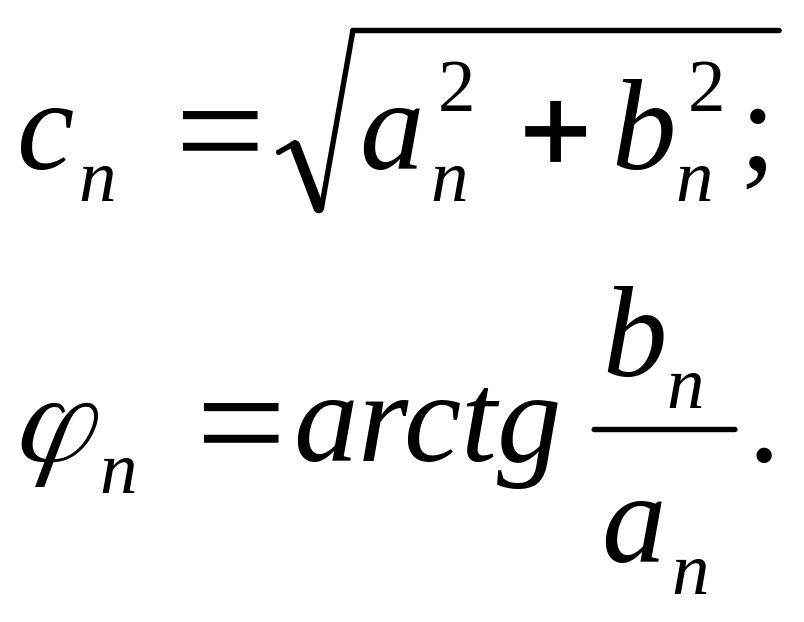
Тобто коефіцієнти ряду Фур’є та коефіцієнти амплітудно-фазової форми ряду Фур’є визначаються співвідношеннями:

, .

З формули (3.9) видно, що полігармонічний процес є сумою сталої складової і нескінченого числа гармонічних складових, які називаються гармоніками і мають амплітуди і фази . Усі частоти гармонічних складових кратні фундаментальній частоті .

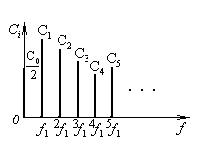
Рисунок 3.2— Спектр полігармонічного процесу

При практичному аналізі періодичних процесів фазові кути переважно не обчислюють. У цьому разі формулу (3.9) можна охарактеризувати тільки дискретним спектром. Іноді полігармонічні процеси містять тільки скінченне число складових. В деяких випадках може не бути фундаментальної складової. Наприклад, нехай періодичний процес утворений сумою трьох гармонічних процесів з частотами 60, 75 і 100 Гц. Найбільший загальний дільник цих частот дорівнює 5 Гц, тобто період цього процесу дорівнює 0,2 с. Тому при розкладанні в ряд Фур’є всі величини дорівнюють нулю, крім значень 12; 15; 20.

Крім тригонометричної і амплітудно-фазової (другий вид тригонометричної) форм, застосовується також запис ряду Фур’є в комплексній формі, яку отримують при зміні тригонометричних функцій показниковими з введенням у розгляд комплексних величин. Для такої заміни використовують формули Ейлера:

з яких випливає:

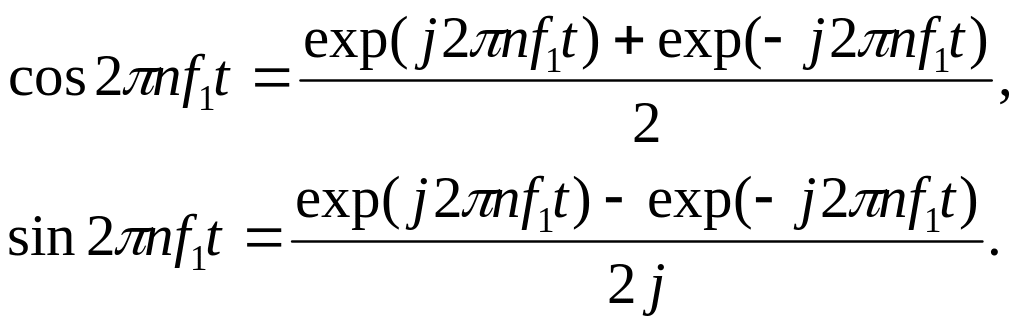
Тоді вираз під знаком суми в (3.5) запишеться так:

Далі вводячи до розгляду комплексно-спряжені величини:

, ,

зведемо ряд Фур’є (3.5) до вигляду:

де .

Оскільки згідно з (3.8) є непарною функцією від , то і:

.

Тоді, підсумовуючи в (3.20) при від до , включаючи (тобто враховуючи і член ряду), приходимо до комплексної форми ряду Фур’є:

;

.

Множина коефіцієнтів ряду Фур’є (3.22) в сукупності утворює спектр функції , а процес їх визначення (3.23) називається спектральним аналізом. Зокрема є середнім значенням функції , а величина , як правило, комплексною амплітудою основної складової або основної гармоніки. Циклічна частота основної гармоніки є величиною, оберненою до періоду основної гармоніки , яка є найменшим ненульовим числом, що задовольняє співвідношенню (3.4).

При величину часто називають комплексною амплітудою -ї гармоніки сигналу . Процес визначення множини іноді називають гармонічним аналізом сигналу .

Формули (3.22) і (3.23) часто називають парою перетворень Фур’є. Формула (3.23) дає змогу визначити спектр, тобто сукупність гармонічних складових, що утворюють суму , а (3.22)— обчислити , якщо задані гармонічні складові (гармоніки).

Комплексну амплітуду (3.23) розраховують при підстановці в формулу (3.19) значень і із (3.7) і (3.8) та використані однієї з формул (3.14)–(3.15).

Оскільки коефіцієнти (3.23) ряду (3.22) є комплексними величинами, то їх можна подати у вигляді:

,

де

або у вигляді

,

де

, , 0, 1, 2, ...