5.2 Методичні рекомендації для розв’язування задач (на прикладах)

Задача 5.1 Проходження детермінованих сигналів через лінійні кола з постійними параметрами.

На диференційну ланку (рис. 5.1) подається сигнал x(t)=Ae^–αt, t≥0; A=10 В; α=4·10⁶ c^–1. Постійна часу ланки T=0,5 мкс. Визначити спектральну щільність сигналу на виході і знайти сигнал y(t) на виході.

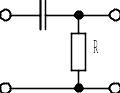
Рисунок 5.1 – Електрична схема диференційної ланки

(до задачі 5.1)

Розв’язування:

Передавальна функція реальної диференційної RC-ланки записується

.

Спектральну щільність вхідного сигналу знаходимо за формулою:

.

Використовуючи формулу (5.3) отримуємо:

.

.

Графіки спектральних щільностей і подані на рис. 5.2 і 5.3.

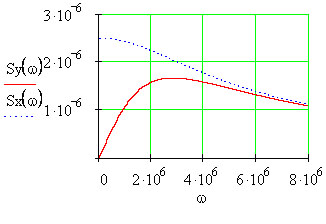
Рисунок 5.2 – АЧХ спектра вихідного сигналу

Рисунок 5.3 – ФЧХ спектра вихідного сигналу

Для визначення імпульсу на виході застосовуємо зворотнє перетворення Фур'є до S_y(ω). Вид отриманої залежності поданий на рис. 5.4

Рисунок 5.4 – Графік сигналу (до задачі 5.1)

Задача 5.2 Проходження випадкових процесів через лінійні ланки.

Нехай на вхід RC-фільтра низької частоти (рис. 5.5) з постійною часу T=RC поступає білий шум. Визначити спектральну щільність, середнє значення квадрату і автокореляційну функцію вихідного процесу.

Рисунок 5.5 – Електрична схема фільтра низької частоти (до задачі 5.2)

Розв’язування:

Вагова функція RC-фільтра НЧ має вигляд:

Тут 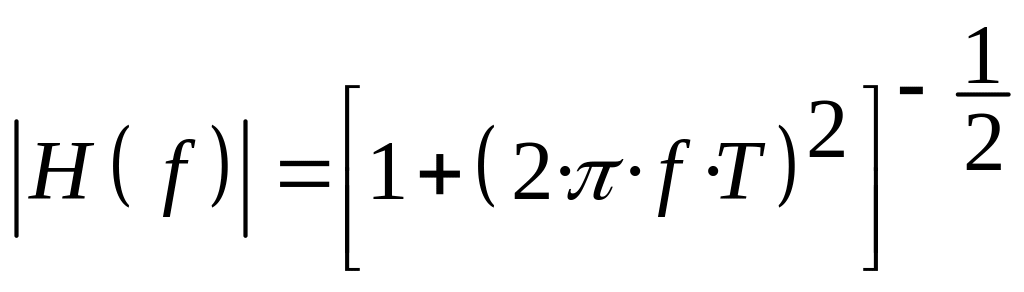— АЧХ.

— ФЧХ.

Із формул та 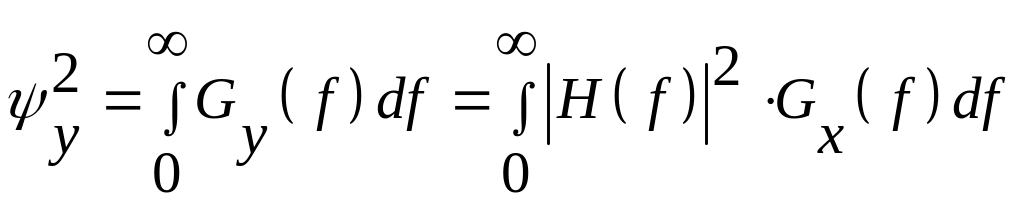слідує, що коли вхідний сигнал — білий шум зі спектром G_x(f)=a при всіх f≥0, то

, 0≤а≤∞

;

.

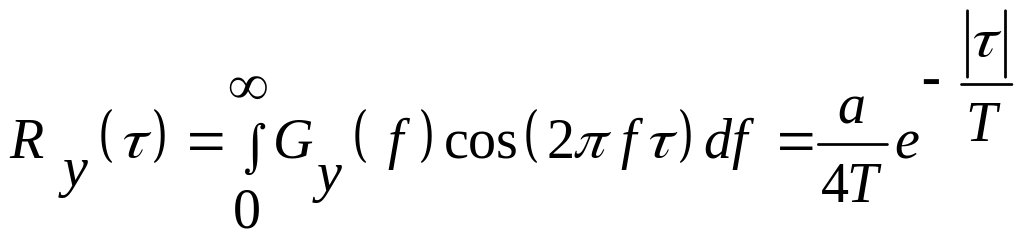Задача 5.3 Реакція ФНЧ на гармонійний процес

Нехай на вхід RC-фільтра низької частоти (рис. 5.5) поступає гармонійний процес зі спектральною щільністю

, де f₀=≥0.

Визначити спектральну щільність, середнє значення квадрату і автокореляційну функцію вихідного процесу.

Розв’язування:

Використовуючи формулу (5.5) отримуємо:

.

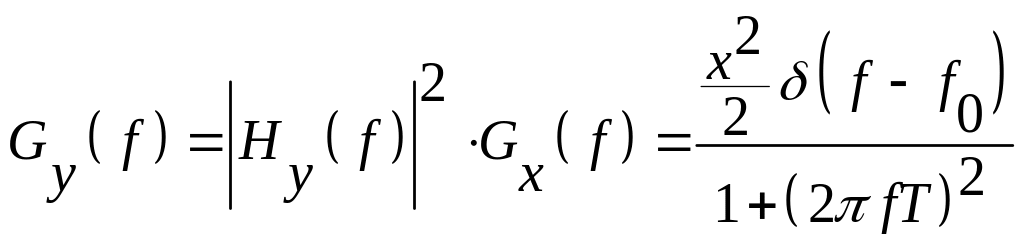Аналогічно з алгоритмом розв’язування задачі 5.2 знаходимо:

;

.

Задача 5.4 На диференційну ланку (рис. 5.1) подається імпульс.

.

Постійна часу ланки RC=2мс. Визначити спектральну щільність сигналу на виході та знайти х_вих(t).

Розв’язування:

Використавши для вихідного сигналу перетворення Фур’є , отримаємо спектральну щільність Помноживши її на , знайдемо і вихідний сигнал

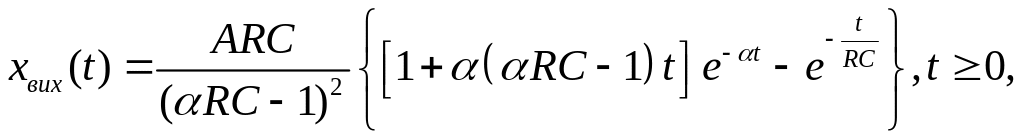
який показаний на рис. 5.6.

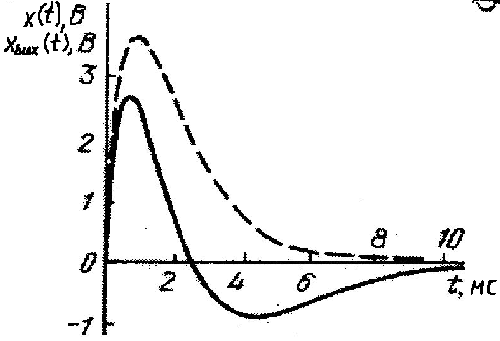
Рисунок 5.6 – Графіки вхідного (пунктир) та вихідного (суцільна лінія) сигналу (до задачі 5.4).

5.3 Завдання для самостійної роботи

Задача 5.5 На інтегральну ланку (рис. 5.7) подається сигнал.

Постійна часу ланки . Визначити спектральну щільність сигналу на виході і знайти x_вих(t).

Рисунок 5.7 – Електрична схема інтегральної ланки

(до задачі 5.5)

Відповідь:

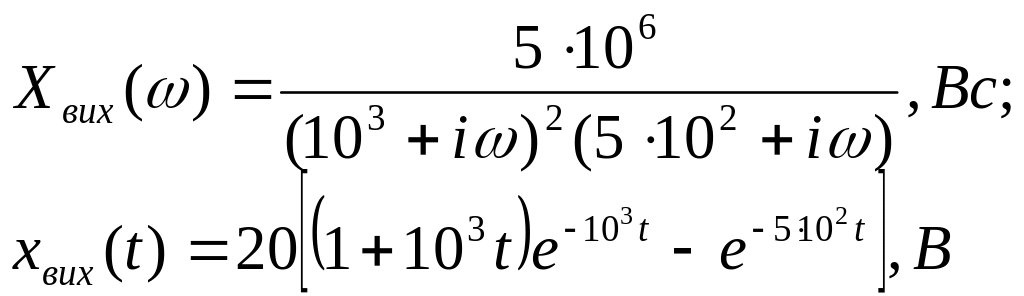
Рисунок 5.8 – Графіки вхідного (пунктир) та вихідного (суцільна лінія) сигналу (до задачі 5.5).

Задача 5.6 На ланку, представлену на рис. 5.9, в момент t=0 подається імпульс Визначити в загальній формі струм .

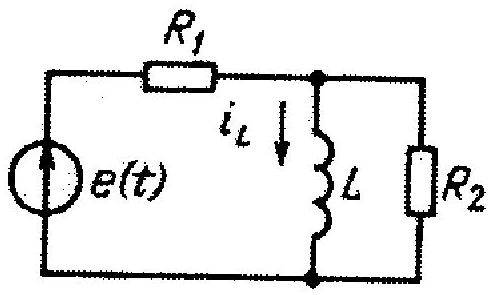
Рисунок 5.9 – Електрична схема ланки (до задачі 5.6)

Відповідь:

Задача 5.7 На ланку, представлену на рис. 5.9, а в момент t=0 подається імпульс.

Визначити в загальній формі струм .

Відповідь:

де