
- •355 Електростатика Розділ 4. Електродинаміка медико-біологічних систем
- •Електростатика
- •4.1.1. Основні характеристики електричного поля
- •4.1.2. Електричний диполь
- •4.1.3. Діелектрики, поляризація діелектриків
- •4.1.4. Діелектричні властивості біологічних тканин
- •4.1.5. П’єзоелектричний ефект
- •Постійний струм. Електропровідність біологічних тканин
- •4.2.1. Характеристики електричного струму
- •4.2.2. Електропровідність біологічних тканин і рідин
- •4.2.3. Дія електричного струму на живий організм
- •Магнітне поле
- •4.3.1. Магнітне поле у вакуумі і його характеристики
- •4.3.2. Закон Біо–Савара–Лапласа
- •4.3.3. Дія магнітного поля на рухомий електричний заряд. Сила Ампера і сила Лоренца
- •4.3.4. Магнітні властивості речовини
- •4.3.5. Магнітні властивості тканин організму, фізичні основи магнітобіології
- •Електромагнітні коливання
- •4.4.1. Рівняння електричних коливань
- •4.4.2. Вимушені електричні коливання, змінний струм
- •4.4.3. Повний опір кола змінного струму (імпеданс). Закон Ома для кола змінного струму
- •4.4.4. Імпеданс біологічних тканин
- •Електромагнітні хвилі
- •4.5.1. Струм зміщення
- •4.5.2. Рівняння Максвелла
- •4.5.3. Плоскі електромагнітні хвилі. Вектор Умова-Пойнтінга
- •4.5.4. Шкала електромагнітних хвиль
- •Семінар “Методика одержання, реєстрації та передачі медико-біологічної інформації”
- •Контрольні питання для підготовки до семінару
- •Додаткова література
- •Типові задачі з еталонами розв’язків
- •Теоретичні питання, що розглядаються на семінарі
- •Додаткові теоретичні відомості
- •4.6.1. Прилади для вимірювання електричних параметрів та їх класифікація
- •Точність вимірювальних приладів
- •4.6.2. Вимірювання сили струму, напруги, ерс, опору в електричному колі
- •Вимірювання опорів
- •Вимірювання невідомої ерс компенсаційним методом. Дільники напруги
- •4.6.3. Осцилографи, генератори, підсилювачі, датчики
- •Підсилення і генерація електричних сигналів
- •Електроди та датчики медико-біологічної інформації
- •Структурна схема кола для одерження, передачі і реєстрації медико-біологічної інформації
- •Завдання для перевірки кінцевого рівня знань
- •Хід роботи
- •Контрольні питання
- •Порядок виконання роботи
- •Контрольні питання
- •Хід роботи
- •Контрольні питання
- •Хід роботи
- •Обробка результатів вимірювань
- •Контрольні питання
Електромагнітні коливання
Електромагнітні коливання – це процеси, в яких такі величини, як заряд, струм, напруженості електричного та магнітного полів тощо, змінюються періодично. Електромагнітні коливання мають дуже широкий спектр практичного використання: майже всі області електротехніки, оптика, радіотехніка. Окремим випадком є електричні коливання.
4.4.1. Рівняння електричних коливань
Розглянемо
коло, до якого входить джерело струму
з електрорушійною
силою
(в загальному випадку – змінною),
індуктивність L, ємність С та
активний опір R, що з’єднані
послідовно (мал. 4.25).
Запишемо вираз, який пов’язує спад
напруги на опорі UR
= IR, напругу на конденсаторі Uc
= q/C, напругу на індуктивності
![]() та е.р.с. джерела :
UR
+ UC
+ UL
=
та е.р.с. джерела :
UR
+ UC
+ UL
=
![]() .
.
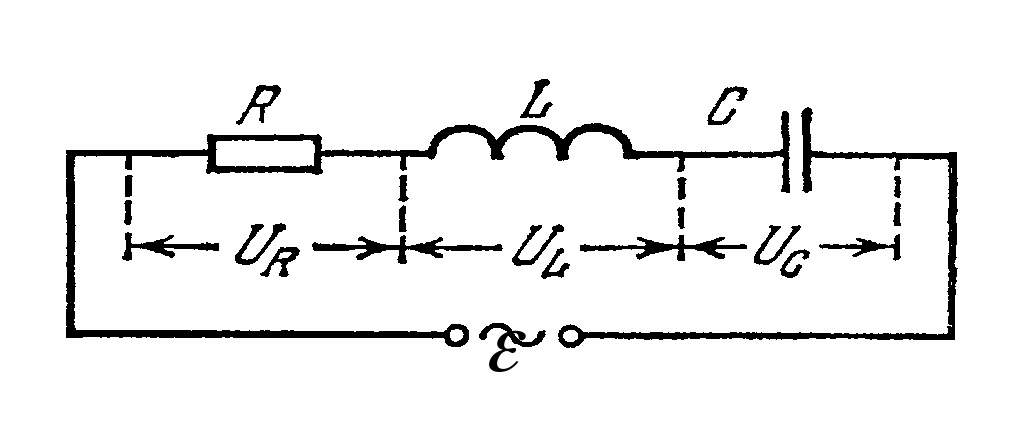
Мал. 4.25.
Оскільки за означенням I = dq/dt, після диференціювання за часом, одержимо диференційне рівняння електричних коливань:
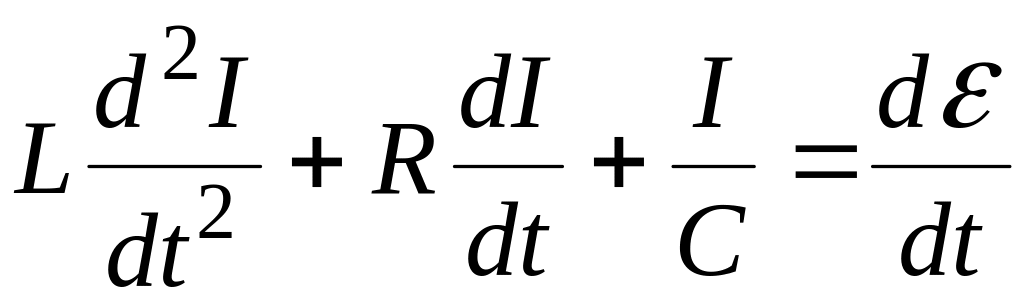 . (4.66)
. (4.66)
Це рівняння виражає залежність сили струму від часу і є лінійним неоднорідним диференційним рівнянням другого порядку з постійними коефіцієнтами. Аналогічне рівняння можна отримати і для інших електричних величин (наприклад, заряду на конденсаторі q).
Вільні гармонічні коливання. Якщо джерело має постійну в часі ЕРС, тобто d/dt = 0, то рівняння (4.66) стає однорідним. За аналогією з механічними коливаннями це є рівняння згасаючих коливань
![]() = 0. (4.67)
= 0. (4.67)
За відсутності опору (R = 0) рівняння (4.67) перетворюється в рівняння вільних гармонічних коливань
![]() .
.
Розділивши ліву частину цього рівняння на L, матимемо:
![]() , (4.68)
, (4.68)
де 0 – власна частота вільних електричних коливань
0
=
![]() . (4.69)
. (4.69)
Рівняння (4.68) має своїм розв’язком гармонічну функцію
I = I0 sin(0t + 0). (4.70)
Вираз, котрий стоїть під знаком синуса (або косинуса), називають фазою коливань . У даному випадку = 0t + 0, де 0 – початкова фаза. Мінімальний проміжок часу, через який фаза повторює своє значення, називається періодом коливань. Період власних коливань
T = 2/0
= 2![]() . (4.71)
. (4.71)
Ця формула носить назву формули Томсона. Із зменшенням індуктивності котушки L та ємності конденсатора С зменшується період коливань, а значить зростає їхня частота.
4.4.2. Вимушені електричні коливання, змінний струм
Р
Мал.
4.26.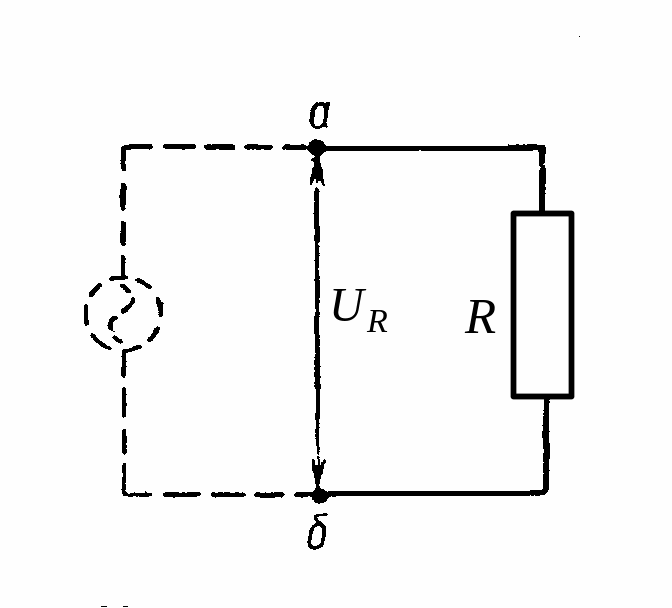
Коло з активним (омічним) опором. Спочатку розглянемо частинний випадок, коли генератор змінного струму замкнений на зовнішнє коло, яке містить лише активний опір R (мал. 4.26). Припустимо, що в колі існує змінний струм:
I = Imsin t.
Застосовуючи закон Ома, визначимо, за яким законом змінюється напруга на активному опорі
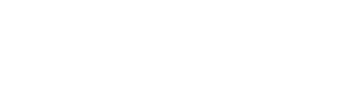 U
= IR
= ImR
sin t
= Umsin
t, Um =
ImR. (4.72)
U
= IR
= ImR
sin t
= Umsin
t, Um =
ImR. (4.72)
Мал. 4.27. |
Мал. 4.28. |
Ця рівність показує, що між коливаннями U та І немає зсуву фаз: напруга і струм одночасно досягають максимальних значень і одночасно перетворюються в нуль (мал. 4.27). Наочно це можна зобразити за допомогою векторної діаграми. Величини, які змінюються за гармонічним законом (U та І), будемо розглядати як вектори, модуль яких дорівнює їхньому амплітудному значенню, а кут між ними – різниці фаз. Вісь діаграми виберемо так, щоб вектор І збігівся з нею за напрямком. Цю вісь називають віссю струмів. Тоді вектор, що зображає коливання напруги, буде направлений вздовж осі струмів (мал. 4.28). Довжина цього вектора Um = = ImR.
К
Мал.
4.29.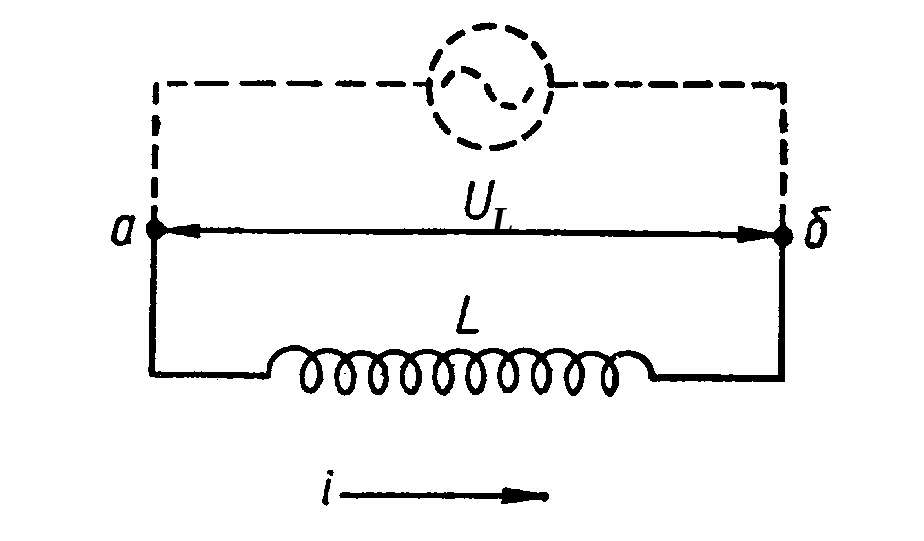
![]()
Якщо сила струму в колі змінюється за законом I = , то для UL отримуємо:
UL = ImLcos t = UmLsin( t + /2), UmL = ImL. (4.73)
Порівнюючи відношення
для амплітудних значень Іm
та Um із
законом Ома, бачимо, що роль опору
відіграє величина
![]() = L,
яку називають індуктивним опором.
= L,
яку називають індуктивним опором.
Т акож
видно, що сила струму I та напруга
U зсунуті за фазою одна відносно
іншої (мал. 4.30) на величину
= /2,
причому напруга в будь-який
момент часу випереджає силу струму. На
векторній діаграмі це зобразиться так,
як показано на мал. 4.31.
акож
видно, що сила струму I та напруга
U зсунуті за фазою одна відносно
іншої (мал. 4.30) на величину
= /2,
причому напруга в будь-який
момент часу випереджає силу струму. На
векторній діаграмі це зобразиться так,
як показано на мал. 4.31.
Мал. 4.30. |
Мал. 4.31. |
Коло з ємністю. Розглянемо третій частинний випадок, коли ділянка кола містить лише конденсатор ємності С (мал. 4.32). Як і раніше, будемо вважати, що сила струму змінюється за законом I = Im sint. Різниця потенціалів між пластинами конденсатора UC = q/C. Але ж сила струму I = dq/dt. Тоді
![]() . (4.74)
. (4.74)
Постійна інтегрування визначає заряд, який не пов’язаний з коливаннями струму, і тому можна покласти q0 = 0. Отже,
UС = – (Іm/C)cos t = UmC sin( t – /2), (4.75)
де UmC = Іm/ C.
П
Мал.
4.32.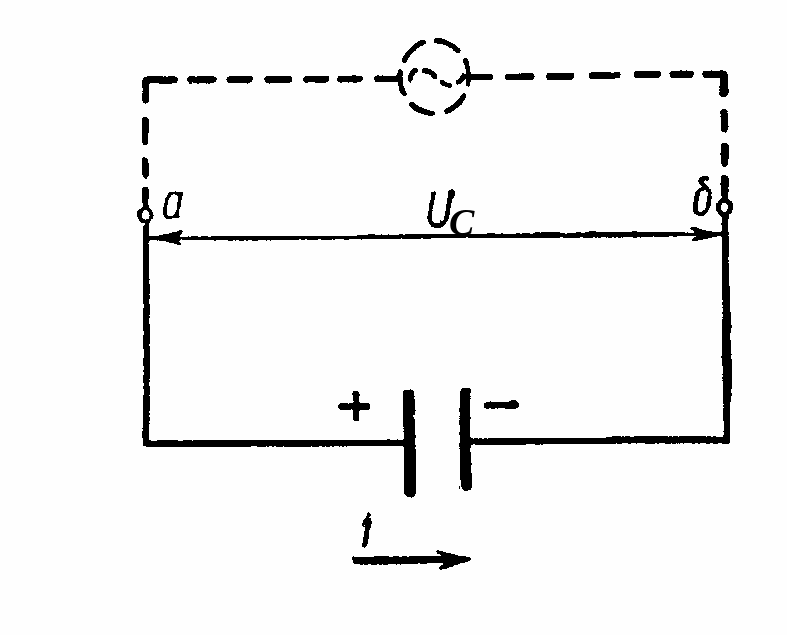
О триманий
результат зобразимо за допомогою
векторної діаграми (мал. 4.34). Вектор, що
відповідає коливанням напруги, повернений
у від’ємному напрямі (за годинниковою
стрілкою) на кут /2.
Довжина вектора дорівнює амплітуді
напруги Im /C.
триманий
результат зобразимо за допомогою
векторної діаграми (мал. 4.34). Вектор, що
відповідає коливанням напруги, повернений
у від’ємному напрямі (за годинниковою
стрілкою) на кут /2.
Довжина вектора дорівнює амплітуді
напруги Im /C.
Мал. 4.33. |
Мал. 4.34. |
