355 Електростатика Розділ 4. Електродинаміка медико-біологічних систем

“Хімія і вчення про магнетизм одне за од­ним визнали провідне значення електрики, і досить ймо­вір­но, що всі явища, які виника­ють під дією сил неорга­нічної матерії, а, можливо, й більшість тих, що стосують­ся рослинного та тваринного жит­тя, вияв­ляться врешті-решт їй підпорядкова­ними”.

Майкл Фарадей

Класична електродинаміка – розділ фізики, що вивчає законо­мір­­ності поведінки електромагнітного поля та його складових – електричного і магнітного полів. Електромаг­ніт­на взаємодія є дуже важливою через широту та різно­манітність її проявів.

Електромагнітні явища мають, окрім свого великого теоретичного значення для розуміння процесів у живій та неживій природі, також і важливі медико-біологічні застосування, серед яких варто виділити:

- дослідження електричних процесів, що відбуваються в живих організмах, а також електричних та магнітних властивостей біоло­гіч­них об’єктів;

- вивчення механізмів взаємодії зовнішніх електромагнітних полів з біологічними тканинами;

- використання сучасної електронної апаратури для потреб медицини та біології.

До вивчення основних законів електродинамічних процесів, що відбуваються в біологічних об’єктах, ми й переходимо.

1. Електростатика

4.1.1. Основні характеристики електричного поля

Електричне поле – це поле, яке створюється електричними зарядами і здійснює взаємодію між ними. Частинним випадком є електростатичне поле; воно створюється нерухомими електричними зарядами, величина яких не зміню­ється з плином часу. Електричне поле можна виявити та дослідити за його дією на інші електричні заряди. З цією метою використовують пробні заряди, величина та розміри яких настільки малі, що вони не викликають перерозподілу зарядів в оточуючих тілах, а, отже, не спотворюють дослід­жу­ване поле.

С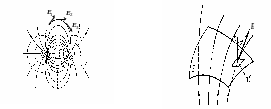 иловою характеристикою електричного поля є, як відомо, напруженість E – векторна величина, яка дорів­нює відношенню сили, що діє з боку поля на розміщений в даній точці пробний заряд q, до величини цього заряду:

E = F/q. (4.1)

Мал. 4.1.

Мал. 4.2.

Розмірність напруженості електричного поля в системі СІ: [E] = Н/Кл = B/м. Графічно електричне поле зображують за допомогою ліній напруженості (силових ліній). Силові лінії – лінії, дотичні до яких в кожній точці електричного поля збігаються з вектором напруженості у цій точці. Силові лінії електростатичного поля незамкнені: вони починаються на позитивних зарядах і закінчуються на негативних або продовжуються у нескінченність (мал. 4.1). Густота силових ліній, тобто їх число на одиницю площі, пропорційна до модуля напруженості.

Скалярну фізичну величину, яка дорівнює dN = EdScos, називають потоком вектора напруженостi елект­ричного поля через поверхню площею dS. Тут  – кут, утворений вектором нормалі до поверхні n і вектором E (мал. 4.2).

Поряд з напруженістю для характеристики електричного поля використовують ще одну векторну величину – електричну індукцію D. Електрична індукція не залежить від діелектричних властивостей середовища, а отже, не змінюється при переході з одного середовища в інше. Для поля у вакуумі:

D =₀E, (4.2)

де ₀ = 8.8510^–12 Ф/м – абсолютна діелектрична проникність вакууму (електрична стала).

Для ізотропного середовища з відносною діелектрич­ною проникністю 

D =₀ E. (4.3)

Розмірність електричної індукції в системі СІ: [D] = (Кл²/H м²)Н/Кл = Кл/м².

Електростатичне поле потенціальне, тобто робота його сил по переміщенню електричного заряду q між двома точками не залежить від форми траєкторії, а визначається лише початковим та кінцевим положеннями заряду. Як відомо, робота сил потенціального поля дорівнює зменшенню потенціальної енергії:

А_12 = W₁ – W₂ = q(₁ – ₂), (4.4)

де  – потенціал. Потенціал – скалярна фізична величина, яка характеризує здатність поля здійснювати роботу і визначається відношенням потенціальної енергії пробного заряду, вміщеного в дану точку поля, до величини цього заряду

 = W/q. (4.5)

Розмірність потенціалу: [] = Дж/Кл = B. Безпосеред­ній фізичний зміст має не сам потенціал, оскільки він, як і потенціальна енергія, визначається з точністю до сталого доданка, а різниця потенціалів. Різниця потенціалів U називається напругою:

U = –  = ₁ – ₂. (4.6)

Геометричне місце точок, що мають однаковий потенціал, називають еквіпотенціальною поверхнею (на мал. 4.1 зображені пунктирними лініями). При переміщенні заряду вздовж еквіпотенці­аль­ної поверхні ( = const, d = 0) робота над зарядом не виконується. Це означає, що сили електрич­ного поля, а отже, і лінії напруженості перпендику­ляр­ні до еквіпотенціальних поверхонь.

Зв’язок між напруженістю і потенціалом. Розгляне­мо переміщення позитивного точко­во­го заряду dl на достат­ньо малу відстань з точки 1 в точку 2, на якій силу F = qE можна вважати постій­ною (мал. 4.3). Тоді робота

d

Мал. 4.3.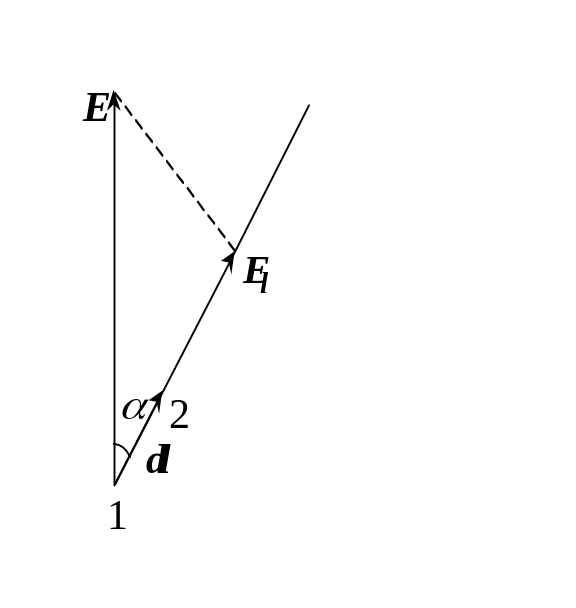

A = Fdlcos = qEdlcos = qE_l, (4.7)

де  – кут між векторами перемі­щен­ня та сили. Припустимо, що через точки 1 та 2 проходять еквіпотенці­аль­ні поверхні з потенціалами ₁ та ₂, тому з іншого боку згідно з (4.4)

dA = q(₁ – ₂) = – qd. (4.8)

Прирівнявши цей вираз та (4.7), матимемо:

E_l = . (4.9)

Це рівняння виражає зв’язок напру­женості електрич­ного поля з потенціалом: проекція вектора напруженості поля на заданий напрям дорівнює швидкості зменшення потенціалу в цьому напрямі. Можна сказати, що вектор напруженості електричного поля в будь-якій точці дорів­нює градієнту потенціала, взятому зі знаком “–“.

E = – grad = – . (4.10)

Таким чином, вектор напруженості електричного поля збігаєть­ся з напрямком найбільшої зміни потенціалу. Знак “–“ у формулі (4.10) показує, що вектор E спрямований в бік зменшення потенціалу.

Якщо поле однорідне (E = const), то остання формула набирає вигляду, відомого з шкільного курсу фізики:

E = (₁ – ₂)/l= U/l, (4.11)

де l – відстань вздовж напрямку E між точками з потенці­ала­ми ₁ та ₂.

Принцип суперпозиції електричних полів. Розгляне­мо сукупність точкових електричних зарядів q₁, q₂, ..., q_n. Кожний із цих зарядів створює власне електричне поле E, незалежно від наявності інших зарядів. Для знаходження результуючого електричного поля в заданій точці застосовується принцип суперпозиції, який полягає в тому, що електричні поля окремих зарядів складаються. Напруже­ність E результуючого електричного поля системи точкових зарядів визначається векторною сумою напруженостей полів E_i, створених окремими зарядами:

. (4.12)

Потенціал результуючого поля  дорівнює алгебраїч­ній сумі потенціалів _i полів, створених окремими точковими зарядами:

 = . (4.13)

Формули (4.12) та (4.13) використовують для обчислення напруженості та потенціалу електричного поля, створеного будь-якими зарядженими тілами.