10.2 Обчислення інтегралів Мора за способом Верещагіна

Обчислення інтегралів Мора суттєво спрощується, якщо одна з епюр пря­молінійна. Така умова завжди виконується для систем, які складаються з пря­мих стержнів, так як епюри від одиничного навантаження обмежені прямими лініями.

Обчислимо інтеграл Мора 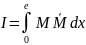, для випадку, коли грузова епюра M від заданого навантаження довільна, а від одиничного навантаження балки зображена прямою, рівняння якої можна записати так

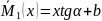(рис. 10.2)

Підставляючи цей вираз у формулу інтеграла Мора, одержимо

(10.2)

Другий інтеграл в (10.2) являє собою площу грузової епюри згинальних моментів М і яку позначимо через

(10.3)

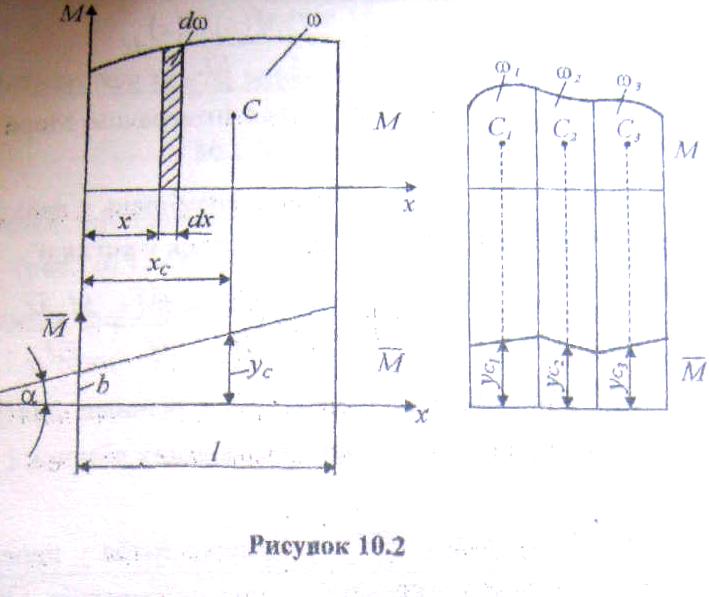
Перший інтеграл в (10.2) — це статичний момент цієї площі відносно осі М, який можна зобразити так:

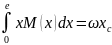(10.4) (10.4)

де х_с — абсциса центра ваги С епюри М

Підставляючи (10.3) і (10.4) в (10.2), одержимо

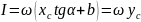(10.5) (10.5)

де у_с — ордината з одиничної епюри , яка береться під центром ваги грузової епюри М.

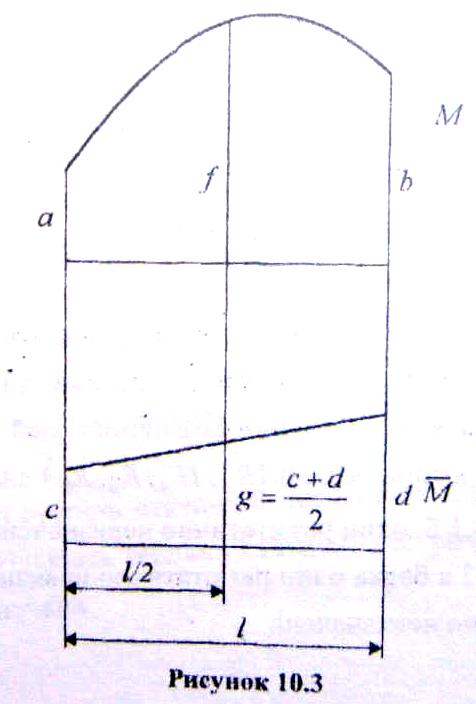
Якщо епюра М — лінія ламана, обчислення інтегралу Мора за формулою (10.5) проводиться по ділянках, на кожній з яких епюра — прямолінійна (рис. 10.3), Тоді

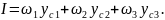
Підставляючи (10.5) в (10.1), одержимо остаточно формулу Верещагіна для визначення переміщень при дії згинальних моментів

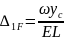(10.6)

10.3 Обчислення інтеграла Мора за формулою Сімпсона-Корноухова

Як відомо з інтегрального числення, якщо проміжок інтегрування l розби-1

ти на дві ділянки, то за формулою Сімпсона

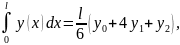(10.7)

Де

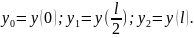
Позначимо M(х)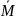 (х)=у(х) і використовуючи для обчислення інтеграла Мора формулу Сімпсона (10. 7), одержуємо

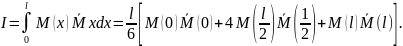(10.8)

Якщо позначити (рис. 10.3)

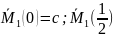M(0)=a; M )=f; M(l)=b; =g;

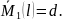
то (10.8) запишеться у вигляді

(10.9)

На таку можливість спрощення обчислення інтеграла Мора вперше вказав український вчений Корноухов, тому і формула (10.9) називається формулою Сімпсона-Корноухова.

У загальному випадку функції y(x) формула Сімgсова (10.7) ‘ наближе­ною. Але якщо підінтегральна функція у(х) с поліномом не вище третього сте­пеня, то формула (10.7) дає точний результат. Отже, якщо М(х) — квадратна парабола, а (х) — лінійна функція, то формула (10.9) є точною.

Формулою (10.9) слід користуватись, коли важко знайти площу або центр ваги грузової епюри М.

Лекція 11 статично невизначені системи

11.1 Ступінь статично невизначеної системи

Як вже раніше вказувалось, статично невизначеними називаються системи, в яких реакції і внутрішні силові фактори не можна знайти тільки з рівнянь ста­тики. В таких системах більше зв'язків, ніж тих, що потрібні для рівноваги. Та­кі зв'язки називаються зайвими, а зусилля в них — зайвими невідомими. Кіль­кість зайвих невідомих вказує ступінь статичної невизначеності системи.

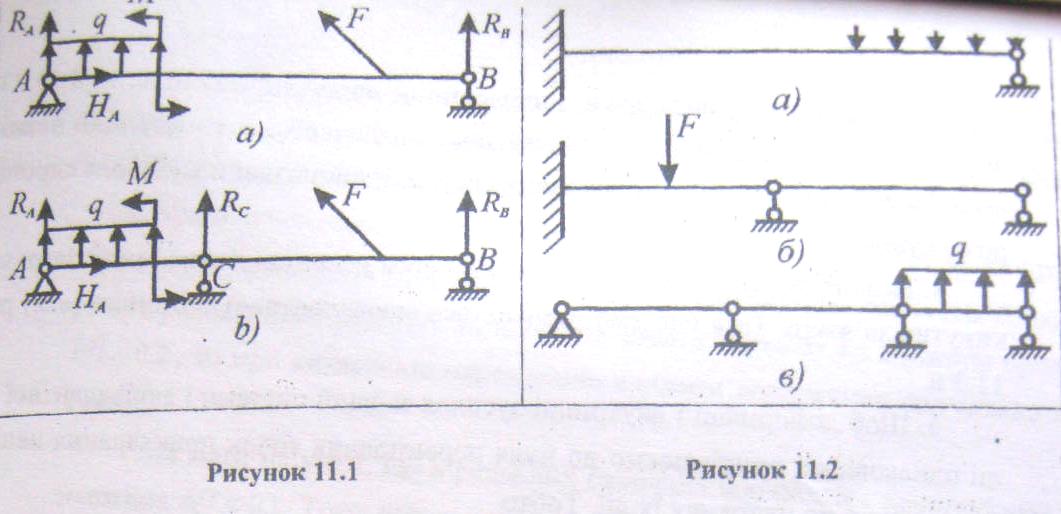
На рис. 11.1а показана балка на двох опорах — система статично визначе­на і геометрично незмінна. Всі три реакції (R_А, Н_А, R_B) визначаються з трьох рівнянь статики. Використовуючи метод перерізів, можна знайти Q(x) і М(х) в довільному перерізі.

Додамо ще один зв'язок, наприклад, шарнірно-рухому опору в перерізі С (рис. 11.1 б). Хоча в результаті цього система стала більш міцною і жорсткою, однак з точки зору геометричної незмінності цей зв'язок зайвий. Тепер з 3 рів­нянь рівноваги чотири реакції (R_А, Н_А, R_В,R_С) знайти не можна. Таким чином, балка на рис. 11.1 б, один раз статично невизначена.

На рис. 11.2 а балка один раз статично невизначена. На рис. 11.2 б, в балки два рази статично не визначені.

N11.2 Канонічні рівняння методу сил

Розрахунок статично невизначеної балки пояснимо на прикладі балки, по­казаної на рис. 11.3 а.

1. Встановлюємо ступінь статичної невизначеності балки. Кількість неві­домих реакцій - 5; кількість рівнянь статики - 3; різниця 5-3=2, отже, балка двічі статично невизначена.

2. Відкидаючи зайві зв'язки, утворюємо основну систему (рис. 11.3 б). Ос­новна система (о.с.) повинна бути статично визначеною і геометрично незмін­ною. Можливі різні варіанти основних систем. Раціональний вибір о.с. спрощує розрахунок.

3. Навантажуємо основну систему заданим навантаженням і реакціями від­кинутих зв'язків. Така система називається еквівалентною системою (е.с.) рис. 11.3 в.

4. Щоб деформації і внутрішні зусилля заданої системи і еквівалентної бу­ли однаковими, прирівнюємо до нуля переміщення точок прикладання невідо­мих реакцій по напрямку їх дії. Тобто

(11.1)

На основі закону незалежності дії сил можна кожне і переміщень 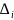зо­бразити як суму переміщень від дії зайвих невідомих і переміщень від дії зада­ного навантаження. Тоді (11.1) набувають вигляду

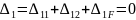
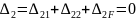(11.2)

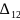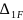- Перший індекс при означає точку і напрямок її переміщення, другий вказує від якого складового фактору шукається переміщення. Наприклад, — це переміщення точки прикладанні сили Х₁ по напрямку ЇЇ дії від сили Х₂; — це переміщення точки прикладання сили X₁ по напрямку її дії від зада­ного навантаження.

Кожне з переміщень 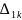можна зобразити як добуток питомого перемі­щення від дії одиничної сиди на величину невідомої сили Х_K

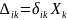
Після підстановки значень переміщень в умову (11.2) одержимо систе­му рівнянь, з яких визначаються невідомі зусилля Х₁ і Х₂

(11.3)

Рівняння (113) називаються канонічними рівняннями методу сил. Така на­зва вказує на те, що ці рівняння записуються за відповідним правилом (кано­ном) і невідомими в цих рівняннях с сили або моменти, які являють собою реа­кції відкинутих зв'язків. Кількість таких рівнянь дорівнює ступеню статичної невизначеності заданої системи.

Питомі переміщення, які мають однакові індекси, називаються головними коефіцієнтами, а питомі переміщення, які мають неоднакові індекси — бічними коефіцієнтами канонічних рівнянь.

Переміщення і , які входять в канонічні рівняння (11.3), як правило визначають за методом Мора або за способом Верещагіна. Якщо для балки або рами прямокутного перерізу відношення висоти перерізу до довжини прольоту 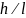<0,2, то при визначенні переміщень впливом поперечних сил можна знех­тувати.

Слід мати на увазі, що в реальних балочних або рамних конструкціях від­ношення h/l < 0,1. Тому при визначенні переміщень за формулою Мора доцільно враховувати лише згинальні моменти. Тоді за формулою (10.1)

;

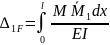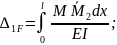
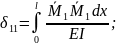
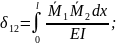
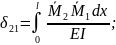
На основі теореми про взаємність переміщень коефіцієнти мають влас­тивість